车用永磁同步电动机的无位置传感器混合控制研究
2013-11-22程金润陆忠东
程金润,陆忠东
(1.上海理工大学,上海200093;2.上海电机学院,上海200245)
0 引 言
永磁同步电动机以其高功率密度、高效率以及良好的动态控制性能而越来越受到关注[1],并广泛用作电动汽车的驱动电机。高性能的永磁同步电动机反馈控制,需要提取转子的位置或速度信号,通常是在转子的轴向安装机械位置传感器(如光电编码器或旋转变压器)来测量转子的位置与速度信息[2]。位置传感器的应用,既增加了系统成本和电机驱动尺寸,又降低了系统的可靠性和对传感器噪声的鲁棒性。为解决上述问题,无位置传感器控制技术得到了广泛的研究和发展。
在电机模型中,可利用定子绕组的输入电流、电压计算反电动势,进而提取转子位置信息。在中、高转速下,此方法简单、低耗,动态性能好;但在低速状态下,定子电阻值的热漂移以及反电动势信噪比过低使得转子位置估算值的精度无法满足要求。在电机定子绕组注入高频测试信号,对因电机结构不对称或铁心饱和引起的凸极进行追踪,可获得对转子位置的估算。此方法适合于电机低速甚至零速下的转子位置估算。
本文在反电动势法与高频注入法的分析研究基础上,采用混合控制策略以实现永磁同步电动机在全速范围内的无传感器控制,即在中、高速采用反电动势法,低、零速采用高频注入法,并提出了线性比例的均值估算对两种方法进行过渡处理,以实现转换过程的平滑切换。
1 高频电压注入法的诠述
1.1 数学模型分析
假设电机定子绕组中感应电动势波形为正弦波,忽略饱和效应、铁损耗以及磁滞等影响,建立永磁同步电动机在高频信号注入下的数学模型。在dq 旋转坐标系下永磁同步电动机的定子电压方程[2]:
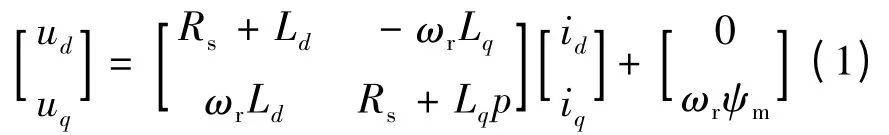
式中:ud、uq为定子d、q 轴的电压;id、iq为定子d、q轴的电流;Ld、Lq为定子d、q 轴的电感;Rs为定子绕组电阻;ωr为转子角速度;p 为微分算子;ψm为转子永磁体磁通。
当注入的脉振电压频率相对于电机基波频率足够高,可将电机模型等价成R-L 模型。同时高频电阻相对于高频电感来说很小,可以忽略。于是可得高频信号注入下的定子电压方程[3]:
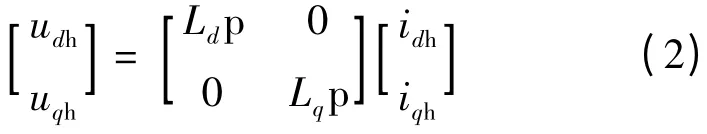
式中:udh、uqh为高频d、q 轴电压;idh、iqh为高频d、q轴电流。
定义估算角度误差:Δθ = θ-。实际转子角度θ、估算角度和估算角度误差Δθ 三者的关系如图1 所示。其中,d-q 为实际同步旋转坐标系,-为估算的同步旋转坐标系,α-β 为实际两相静止坐标系。
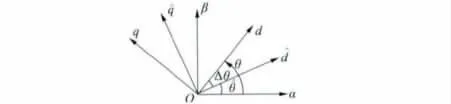
图1 坐标关系图
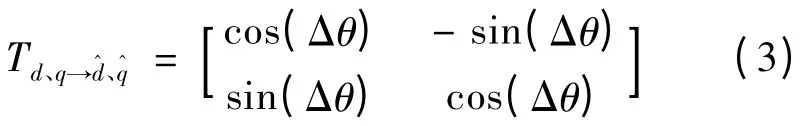
在估算的同步旋转坐标系直轴上注入高频余弦电压信号umhcos(ωht),得到估算的电流响应:
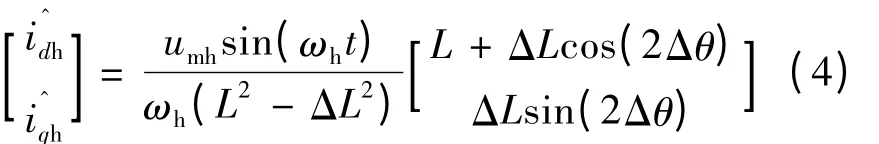
式中:umh为高频电压幅值;ωh为高频注入电压的角频率;
1.2 转子位置信息的提取
三相电流经过坐标变换得到q 轴电流,通过带通滤波器(BPF)得到q 轴电流的高频分量,然后与调制信号sin(ωht)相乘,再经低通滤波后得到调节器所需的输入量f(Δθ),如图2 所示。当Δθ 很小时,sin(2Δθ)= 2Δθ,则:
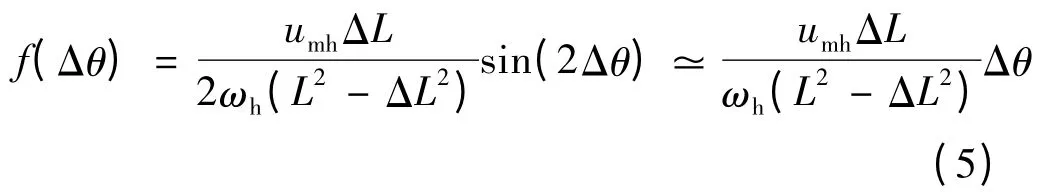
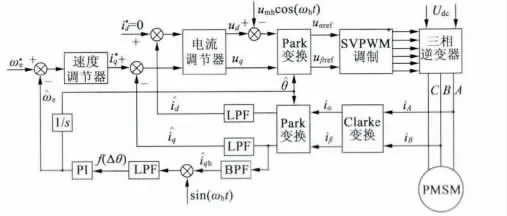
图2 注入法系统控制结构图
由于f(Δθ)与Δθ 成正比,可通过一个锁相环(PLL)控制器得到估计的转子位置,将引入到控制系统的坐标变换模块中,形成位置闭环估计[3]。
1.3 转子极性的判断
由于高频信号注入法无法判断初始时刻下的转子永磁体极性,如果估算角度与实际位置相差π,则估计极性与实际极性相反,会造成电机反转。因此,需要在初始时刻判断转子极性方向,以获得正确的转子角度。通常利用磁路的饱和效应来判断转子极性。
在不确定转子磁极方向的情况下,Δθ 可能取值为0 或π,此时式(4)中高频响应电流的直轴分量:态方直下向轴
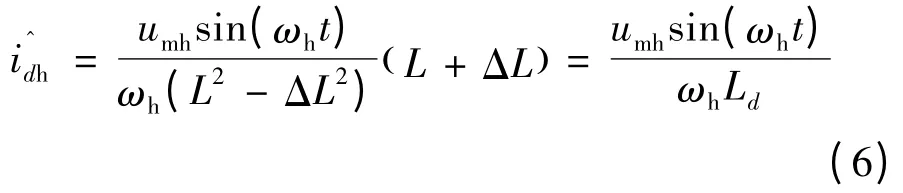
2 基于反电动势法的转子位置估算
由于高频注入法通过外部激励实现,本身具有一定的复杂性,再结合反电动势法形成混合控制,使得系统复杂性进一步增加,会对系统的稳定性与动态响应时间产生不利影响。本文采用简单的反电动势直接估算法和磁场定向控制id= 0 策略,但需要做出相应的误差补偿,提高估算的精度。
采用反电动势估算转子位置法较磁链估算法的优势在于,避免了纯积分器使用带来的参数漂移。两相定子坐标系下,反电动势的空间矢量可表示:
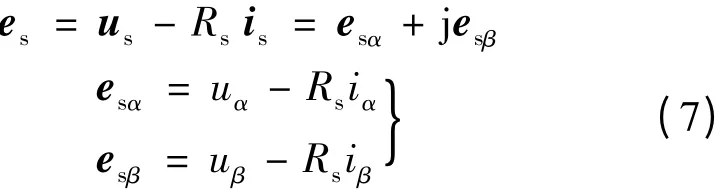
式中:us、is为定子电压、电流的空间矢量;esα、esβ为反电动势空间矢量在α、β 坐标系下的分量。
在id= 0 控制策略下,电机模型处于稳定状态下,转子位置的估算表达式:
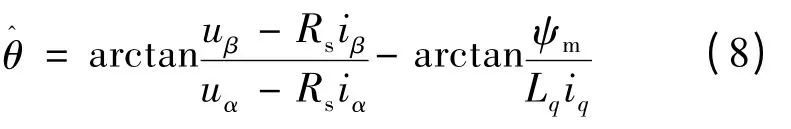
因此,需要确立一个估算控制回路来消除位置角估算的稳态误差。
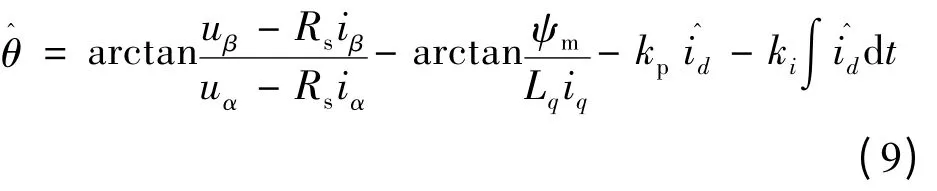
式中:kp、ki为比例积分参数。
反电动势估算法结构如图3 所示。
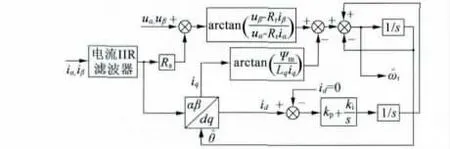
图3 反电动势算法结构图
3 无位置传感器的混合控制
式(9)表示了反电动势法估算转子角度的数学方程。当电机在中高速稳定运行时,定子绕组电阻的热漂移可以忽略不计;但当电机进入低速阶段,在恒转矩控制下,端电压随频率同步降低,信噪比不足以及定子电阻的变化会引起较大误差。结合高频信号注入法在低速段对转子角度估算的优势,可形成混合的无传感器控制,实现电机全速范围内的转子位置与速度估算。
为了实现两种估算法的平滑切换,在一定的速度区域,对两种方法求得的估计值进行均值计算。我们设定在20% 的额定速度以下只采用注入估算法;在40% 的额定速度以上只采用反电动势估算法;在20%~40% 的额定速度之间,混合算法对两种方法获得的估算值进行线性比例均值处理。设kω为瞬时速度对额定速度的百分比,转子位置角的估算均值可表示:
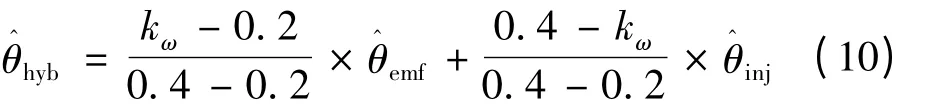
式中:kω∈[0.2,0.4]。
从式(10)中可以看出,当速度超过20% 时,注入法估算值在均值中的比重呈线性递减;当速度达到40% 时,反电动势估算法独立运行,此时,应切断高频注入信号,以避免额外的损耗与干扰。
永磁同步电动机的混合无传感器控制模型如图4 所示,在磁场定向控制id= 0 策略下,采用电流追踪型永磁同步电动机变频器供电,可以实现平滑转矩控制。这种控制具有转矩/惯性比大、快速加减速时可提供很高的冲击转矩、低速转矩平滑、零速性能好等优点[7]。控制模型中,估算的位置与速度参数被反馈到系统的电流环与速度环控制,电流环周期为100 μs,速度环周期为5 ms,并加入一个PWM 周期的延迟。
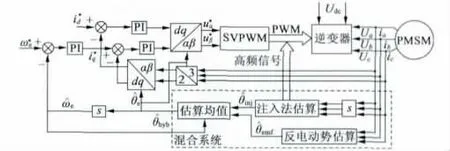
图4 混合无传感器控制系统模型
4 试验结果
本文通过MATLAB /Simulink 软件下的xPC Target 功能包,对永磁同步电动机的混合无传感器控制算法进行实时仿真测试,并建立“双机”模式,即对目标机的配置与启动,主机对目标机的实时控制。在主机上实现模型的建立、离线仿真和代码编译;而目标机在安装实时内核后,成为实时控制器,在目标机的PCI 槽上安装数据采集卡。主机与目标机通过TCP/IP 进行通讯。其结构框图如图5 所示。

图5 xPC Target 双机模式控制结构
“双机”模式的硬件配置:一台主机,普通的笔记本即可,需要安装MATLAB、Simulink、RTW 以及C 编译器;一台基于x86 架构的工控机作为目标机,需安装NI 的数据采集卡PCI -6024E DAQ 用于检测定子电流和输出PWM 信号(软件生成);一个1 024分辨率的编码器用来检测转子的实际位置与速度。
为了便于试验,本文采用小容量永磁同步电动机,并非实际车用驱动电机,其参数:额定功率3.8 kW,极对数3,额定转速2 000 r/min,定子电阻0.5 Ω,直轴电感4.35 mH,交轴电感5.9 mH,永磁体磁通0.084 Wb,注入高频电压幅值20 V,频率取1 kHz。与此同时,一个同等功率的感应电机用来作为负载。
用于电动汽车驱动的永磁同步电动机,无论是起停、加减速状态,都是带负载运行,且因为汽车行驶环境的不同,负载的变化极其复杂,本文简化了负载条件,在额定负载的状态下,对永磁同步电动机的无传感器恒转矩控制进行仿真测试,并给出转子位置估算的误差。
图6 显示了额定负载下的电机在零速、30% 转速(600 r/min)、全速下的转速波形和转子角度误差。在零速和全速下,分别只采用高频注入法和反电动势法估算转子位置;而在30% 速度时,则采用混合算法求取前述两种方法估算值的均值。
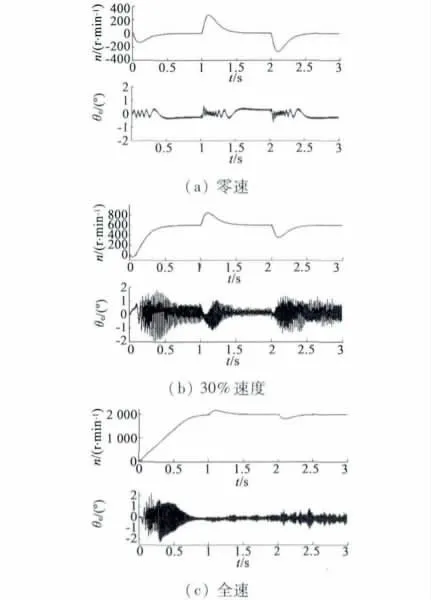
图6 转速波形与转子角误差
在零速下,高频注入法获得了很好的转子角度估算效果,误差较小,不到0.5°电角度,只有转速信号波动带来的轻微误差震荡。在转子速度由0 上升到20% 转速(400 r/min)之后,误差与震荡程度明显增加;当转速稳定时,误差值亦开始减小;随着时间的推移和电机热效应的影响,定子电阻值的热漂移导致转子角度误差有增大的趋势。在转速由0 上升到全速的过程中,在进入混合估算模式后,误差增大,并缓慢减小;当速度达到40%(800 r/min)时,脱离混合模式,误差又增大,但旋即迅速减小;在电机全速稳定运转时,转速脉动以及定子电阻的变化所引起的误差,相比图6(b)显示要小得多,此时的电机数学模型更接近理论状态。
5 结 语
本文对永磁同步电动机的无位置传感器混合控制作了初步的研究和探索,在中高速区域,反电动势法以其简单易用,获得了对转子角度与速度的有效估计;而在低、零速区域,则应用高频信号注入法,弥补了反电动势法在低速下估算转子位置的致命缺陷。实现了永磁同步电动机在全速范围内的无位置传感器控制。本文通过设定一个速度缓冲区,在此区域内,对两种估算值进行线性的均值计算,以实现两种估算方法的平滑过渡。实验结果表明,尽管在混合模式与两种方法切换过程的瞬时状态下,转子角度的误差明显增大,但始终保持在2°电角度范围内,并在完成切换后,迅速减小,证明了混合模式对消除切换脉动的有效性。
[1] Widyan M S,Hanitsch R E.High-power density rapid-flux permanent sinusoidal three-phase three slot four-pole electrical generator[J].International Journal of Electrical Power & Energy Systems,2012;43:1221-1227.
[2] Frederik M,Sergeant P,Melkebeek J A.A sensorless PMSM drive using modified high-frequency test pulse sequences for the purpose of a discrete-time current controller with fixed sampling frequency[J].Mathematics and Computers in Simulation,2010,81(2):367-381.
[3] 刘毅,贺益康,秦峰.基于转子凸极跟踪的无位置传感器永磁同步电机矢量控制研究[J].中国电机工程学报,2005,17(25):121-126.
[4] 干瑞,朱元,王双全.永磁同步电机静止及低速下无传感器控制研究[J].微电机,2012,45(12):66-69.
[5] 李计亮,高琳.考虑磁路饱和的永磁同步电机弱磁调速系统仿真[J].微电机,2010(12):62-65.
[6] Genduso F,Miceli R,Rando C,et al.Back EMF sensorless-control algorithm for high-dynamic performance PMSM[J].IEEE Transations on Industrial Electronics,2010,57(6):2092-2100.
[7] 黄立培.电动机控制[M].北京:清华大学出版社,2003.
