某大口径火炮复进开闩阻力动力学分析

付 帅，顾克秋，张俊飞

(南京理工大学 机械工程学院,江苏 南京 210094)

大口径火炮在复进过程中，开闩凸轮撞击开闩板，开闩板对开闩凸轮产生阻力，该阻力在身管轴线方向上的分量即叫做开闩阻力。开闩阻力的大小不同，对复进特性的影响也不同。开闩阻力过大，曲柄受到的载荷就越大，曲柄容易产生疲劳断裂，而且会对复进稳定性造成影响；开闩阻力过小，对复进速度的影响较小，不能达到降低复进速度的目的，同时，复进速度过大，复进稳定性同样也会不好。对开闩阻力的研究，能够为研究复进特性提供更好的依据，提高复进稳定性。

1 数学模型

1.1 开闩基本动作

在火炮复进到一定程度时，开闩凸轮和开闩板发生撞击，迫使曲轴转动，带动曲臂向后转，曲臂滑轮下压闩体，使闩体在炮尾滑槽内移动。与此同时，曲轴的转动带动关闭杠杆，关闭杠杆轮在支筒横槽内下压支筒，使得支筒下移，对关闩簧造成挤压，储存关闩能量。闩体继续向下运动，由于闩体两侧的定形槽、炮尾的圆弧槽和身管后端面的约束作用，这就使得抽筒子只能按照预定的轨迹运动，当抽筒子运动到闩体上部圆弧槽时发生剧烈抽壳动作，实现抛壳[1]。

1.2 理论关闩簧力

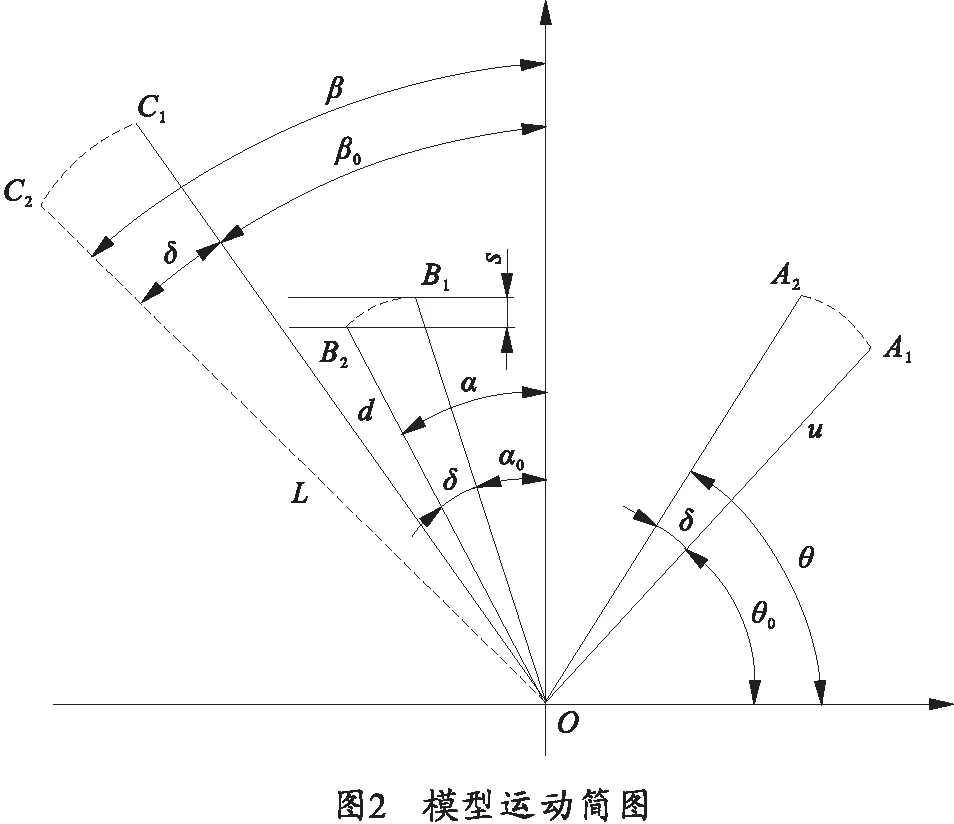
在图2中，OA1、OB1、OC1分别代表曲柄、关闭杠杆、曲臂的初始位置，A1、B1、C1分别为曲柄凸轮圆心、关闭杠杆和曲臂滑轮的圆心，OA2、OB2、OC2分别代表曲柄、关闭杠杆、曲臂转动δ角度的位置。OA1和水平线的夹角为θ0，OB1和竖直线的夹角为α0，OC1和竖直线的夹角为β0，由于曲臂和关闭杠杆都是通过花键和曲轴相联接，所以它们没有相对转动，它们共同转动角度为δ。由图2可知，θ、α、β及其初始值θ0、α0、β0之间存在着简单的关系：

θ=θ0+δ,α=α0+δ,β=β0+δ

(1)

式(1)变形可得：

δ=θ-θ0,α=α0+θ-θ0,β=β0+θ-θ0

(2)

由式(2)可以看出，θ为α和β的基本变量，所以关闭杠杆下压支筒，只和曲柄转过的角度有关。在图2中，OA=u，OB=d，OC=L，假设关闩簧的初始弹簧力为F0，弹簧末力为F，支筒下移距离为s，所以弹簧所受力为：

F=F0+ks

(3)

式中：k为弹簧刚度，可根据式(4)进行计算：

第三阶段，由岗位分析深入岗位评价，从2016年开始，医院人事处在重新梳理各岗位说明书的过程中，进一步对20多个职能部门200多个岗位的岗位目的、职责、权限、工作关系、任职资格等信息予以了清晰描述。以此为基础，人事处着手进行岗位评价的推进工作。

(4)

G为弹簧材料的切变模量；d0为弹簧丝直径；D2为弹簧直径；n为弹簧有效圈数。

根据图2中的转动关系，可得：

s=dcosα0-dcosα=d[cosα0-cos(θ+α0-θ0)]

(5)

把式(4)、式(5)代入式(3)得：

(6)

本模型中，G取8×104MPa，d0=7 mm，D2=40 mm，n=39，d=80 mm，α0=20°，θ0=48°，F0=0，根据曲柄凸轮和开闩板的位置可以计算出，曲柄须转过116°才能实现开闩，所以θ=164°时才能彻底开闩。把这些数据代入到式(6)可得关闩簧最大受力为22 281.7 N。计算关闩簧力，是计算开闩阻力、从理论上进一步计算解决炮尾炮闩其他受力问题所必须的。

2 动力学模型

在炮闩模型中存在着很多碰撞，炮闩机构大多数都是通过碰撞来传递力与力矩。研究多体系统的碰撞问题主要有广义动量平衡法和等效弹簧阻尼模型法[2]。运用广义动量平衡法时，需假设碰撞时间很短，碰撞力不随时间的变化而变化，效率较高；运用等效弹簧阻尼模型法时，不需认为碰撞时间很短，需对动力学方程积分计算，所以效率较低。冲量动量法无法求解出碰撞力在碰撞过程中随时间的变化；而等效弹簧阻尼模型法对动力学方程积分，可以求出随时间变化的碰撞力，但是在碰撞结束时会出现阻尼不为零的情况[3]。

2.1 模型中的假设

1)为了简化模型，假设摇架固定，即摇架不随火炮后坐、复进摆动，身管在摇架上无振动的沿炮膛轴线滑动。

2)不考虑火炮后坐部分，假设只从后坐最大位移处复进开始，只计算复进过程。

3)根据相关参数，用ADAMS编程复进机力、制退机力及相关摩擦力。

2.2 炮尾炮闩零件间的拓扑关系

设定全局坐标系为：原点位于ADAMS/VIEW平台的缺省坐标原点(0,0,0)，在模型中为炮尾后端面圆的圆心。x轴沿0°射角时的炮膛轴线，且指向炮口为正，y轴沿铅垂向上为正，z轴按右手定则确定[4]。炮尾系统共有26个刚体，其主要拓扑结构关系如下：

身管和摇架采用移动副联接，身管和炮尾采用固接铰联接；开启杠杆和炮尾、开启杠杆和拉杆、拉杆和曲柄采用转动副联接；曲轴和炮尾采用转动副联接；曲轴和曲臂、曲轴和关闭杠杆、曲柄和曲轴采用固铰联接；在关闭杠杆和支筒之间、曲臂轮和闩体采用碰撞接触联接；支筒和炮尾采用移动副联接；左、右抽筒子分别和炮尾、身管、闩体建立碰撞接触联接；并在左、右抽筒子和闩体之间建立平面副联接；闩体和炮尾建立滑动副联接；药筒和身管、抽筒子、闩体建立接触碰撞联接。另外，击发装置、保险装置及档弹装置等和炮尾、闩体也建立的正确的联接关系。实体三维模型如图3所示，图中隐藏了炮尾、闩体及其他一些不重要的零部件。

在模型中，前0.2 s为静态步，目的是为了使部分零件在重力作用下趋于稳定，模型中的时间减去0.2 s，即为火炮复进时间。此外，模型中的复进机力、制退机力由工厂提供，并且通过ADAMS编程，实现复进机力和制退机力的控制。本模型只分析计算高低射角、 方向射角时的开闩阻力特性。

3 动力学特性研究

3.1 开闩特性

3.1.1 复进速度及开闩阻力

后坐体在复进机力的作用下进行复进，制退机力作为阻力作用在后坐体上。支筒下压关闩簧，开闩簧对支筒有反作用力；曲臂转动时要克服闩体和炮尾之间的摩擦力；抽壳时，药筒对抽筒子有较大的作用力，这些力都会阻碍曲柄转动，产生开闩阻力。

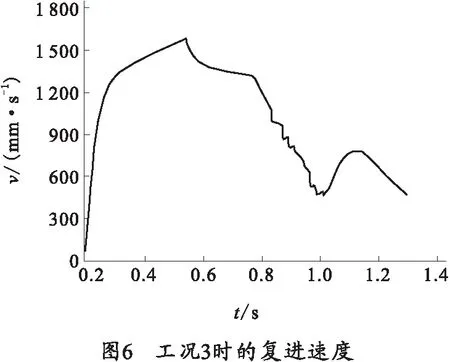
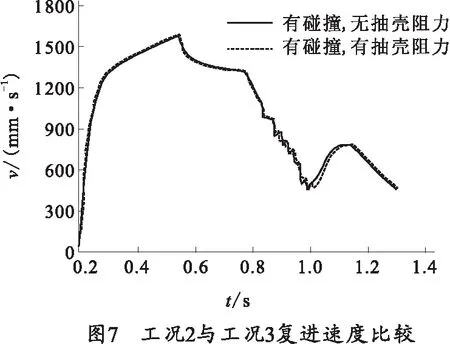
笔者分析了3个工况：工况1，曲柄不和开闩板相碰(不建立碰撞)、不添加抽壳阻力；工况2，曲柄和开闩板发生碰撞、但无抽壳阻力，即不抽壳；工况3，曲柄和开闩板发生碰撞，最大抽壳阻力为2 kN。工况1～3情况下的复进速度如图4～图6所示。工况2和工况3时的复进速度比较如图7所示。在目前的火炮动力学分析中，大多都没有考虑炮闩系统内的碰撞，其复进速度特性和图4所示的曲线较为相似。

以工况2来分析，工况2时的开闩阻力和复进速度部分时间下的图形如图8所示。开闩凸轮与开门板撞击过程中碰撞力出现三次明显的峰值，且撞击过程中凸轮与开门板有明显的脱离[5]。开闩凸轮撞击开闩板，第一次由于关闩簧没有储存能力，因此用很小的力就可以把开闩凸轮撞开，形成开闩阻力的第一个波峰；后坐体继续复进，开闩凸轮和开闩板第二次撞击，关闩簧开始逐渐储存能力，撞击力比较大，但关闩簧储存能量刚处于初始阶段，开闩凸轮被撞开的时间比较长，形成开闩阻力的第二个波峰；第三次撞击，关闩簧被压缩了一定距离，需要较大的力把开闩凸轮撞开，但时间较短，形成开闩阻力的第三次波峰；在以后的过程中，开闩凸轮和开闩板基本处于贴合状态，开闩阻力的震动和关闩簧的阻尼有关，并呈现波动上升趋势。

每一次撞击都会降低复进速度，在图8中，每一次撞击都使得速度降低。由于第一次撞击力较小，而且撞击时间短，速度下降不明显。在开闩阻力逐渐波动减小的时候，即开闩动作基本到位后，复进速度在复进合力(制退机力、复进机力、相关摩擦力等的合力)的作用下会逐渐回升，然后再下降。

以工况3来分析，开闩阻力和复进速度曲线如图9所示。与图8相比较，图9中复进开闩速度在0.92 s到0.975 s之间变化较平稳，开闩阻力的振动也较小，这是因为在这一时间段，抽壳阻力产生了作用。抽壳力作用在抽筒子的承载面上，抽筒子同时又对闩体有作用，阻碍着闩体下移，阻碍开闩。

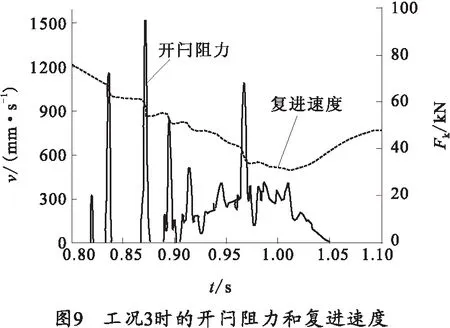
图8与图9相比较，还可以发现，在开闩阻力下降阶段，图8中的阻力曲线波动较小，图9中的阻力曲线波动较大，这是因为图9中的模型受到了抽壳阻力的作用。抽筒子在完成抽壳动作过程后，抽壳阻力是非线性逐渐减小的，在抽壳阻力减小时，抽筒子上的作用力同时减小，关闩簧能力适当释放，造成振荡，这种振荡可以通过增大弹簧阻尼来控制。

3.1.2 不同抽壳阻力对开闩阻力的影响

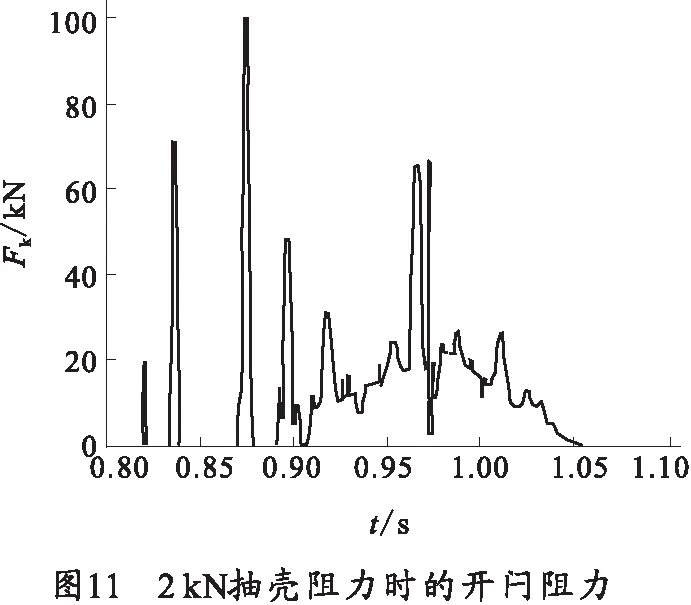
由于制造工艺的误差，及药筒火药爆炸后药筒和药室内壁贴合程度不同，会使药筒和药室内壁间的摩擦也不同，所以，每次开闩阻力也不尽相同。笔者研究了最大抽壳阻力分别为1、2、4 kN时的开闩阻力，如图10～图12所示。在缓慢抽壳过程中，由于最大摩擦力不同，作用在抽筒子上的力不同，开闩凸轮开始撞击开闩板时刻的阻力也不同，机构在0.965 s左右开始剧烈抽壳，由图中可以看出，抽壳阻力越大，在抽壳过程中开闩阻力的振荡越大，抽壳阻力为4 kN时的开闩阻力在后期比前两种情况振荡的厉害。

3.2 复进过程合力分析

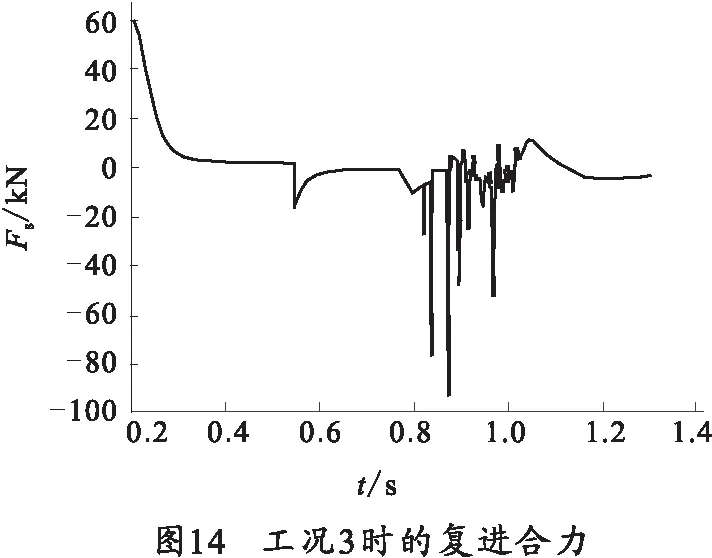
研究复进问题，必须对后坐部分进行受力分析，由于模型是沿身管轴线方向运动的，复进时无需克服重力，复进合力等于剩余复进力减去液压阻力，再减去开闩阻力，根据公式Fs=Ff-FΦfy-F-FT-Fk可知[6]，产生复进加速度的根本因素是复进合力，复进合力Fs由复进机力Ff、反后坐装置复进液压阻力FΦfy、相关摩擦力F、FT和开闩阻力Fk共同作用提供的，由于抽壳阻力的作用物是药筒，而作用在药筒上的摩擦力由身管提供，抽筒子、身管都是后坐体的一部分，所示抽壳阻力是整个后坐体系统的内力，不参与复进合力的合成计算。图13、图14分别是工况2、工况3时的复进合力，对比图5，图6，每一次速度的变化，都是在复进合力的作用下发生的。

研究复进合力，对研究复进时火炮的稳定性和静止性具有重要意义，确保后坐体能够平稳的复进到位，能够保证火炮射击精度和射击密集度，提高发射速度，同时能更好的设计复进特性。

4 结束语

笔者通过理论分析，利用虚拟样机ADAMS软件建立了简单的开闩数学模型，模拟了某火炮局部样机的开闩动作过程，对这一复杂的过程进行了仿真，通过分析工况1、工况2和工况3时的开闩阻力特性及复进速度特性，探讨了不同情况下开闩阻力对复进速度的影响，并根据对复进合力的分析，研究了实际模型中影响复进合力的因素。这为以后完善改进全炮动力学模型提供了参考和借鉴，解决了以往模糊的开闩阻力问题，为研究炮尾炮闩其他零部件的动态特性打下了基础。

[1] 方怡宏.火炮结构教程[M].南京：华东工学院,1991:200-202.

FANG Yi-hong. Artillery structure tutorial[M].Nanjing: East China Institude of Technology, 1991:200-202.(in Chinese)

[2] 石明全,刘雷,陈运生.火炮开闩过程动力学分析[J].弹道学报,2003,15(2):17-22.

SHI Ming-quan, LIU Lei, CHEN Yun-sheng. Research on process of opening block and ejecting container of a certain gun[J].Journal of Ballistics, 2003,15(2):17-22. (in Chinese)

[3] 董富祥,洪嘉振.多体系统动力学碰撞问题研究综述[J].力学进展,2009,39(3):352-358.

DONG Fu-xiang, HONG Jia-zhen. Review of impact problem for dynamics of multibody system[J].Advances in Mechanics, 2009,39(3):352-358. (in Chinese)

[4] 周成.轻量化牵引火炮动力学分析与优化研究[D]. 南京:南京理工大学,2011.

ZHOU Cheng. Kinetic analysis and optimization research on lightweight towed howitzer[D]. Nanjing:Nanjing University of Science and Technology, 2011. (in Chinese)

[5] 杜中华,王兴贵,马吉胜.基于虚拟样机技术的某型火炮开门过程动力学特性研究[J].机械工程学报,2004,40(6):123-126.

DU Zhong-hua,WANG Xing-gui,MA Ji-sheng. Research on gun’s breech-opening process dynamic characteristics based on prototype technology[J].Chinese Journal of Mechanical Engineering, 2004,40(6):123-126. (in Chinese)

[6] 高树滋,陈运生,张月林,等.火炮反后坐装置设计[M].北京:兵器工业出版社,1995:155.

GAO Shu-zi, CHEN Yun-sheng, ZHANG Yue-lin,et al.Design of recoil system for guns[M].Beijing:The Publishing House of Ordnance Industry, 1995:155. (in Chinese)