一种防空武器发射装置平衡机优化设计混合算法

韩 勇，王 洁，程永强，2，任卫华，吕 爽

(1.空军工程大学 防空反导学院，陕西 西安 710051;2.西北工业大学 航海学院，陕西 西安 710072;3.中国飞机强度研究所，陕西 西安 710065)

平衡机是防空武器发射装置的重要组成部分，在变角度发射装置中，其作用至关重要，它的性能严重制约着武器系统的打击精度和效率。由于防空武器威力的不断提高，弹体长度和质量都会发生很大的变化，因此对平衡机的结构进行优化设计从而改善其性能显得十分迫切[1]。

平衡机优化问题属于极大极小值(minimax)问题，这种问题具有非常广泛的应用。许多决策问题都可以转化为minimax问题，而且大量的车辆工程、工程优化、资源分配等问题同样都是转化成minimax问题来求解的[2-4]。在minimax问题中，目标函数包含极大项，因此它是连续但不可微的，这就以梯度为基础的传统方法求解带来了困难。当前国内外学术界针对该问题提出了许多算法，如：次梯度法，SQP，SELQP等数值解法[5-6]。然而近年来国内进行平衡机优化设计时通常采用的是单纯形法，复合形法，虽然取得了一定的效果，但是算法求解复杂，而且精度较低。文献[7]在求解minimax问题时，通过引入极大熵法将模型转化为光滑的连续极值问题并取得了较好的效果。遗传算法在求解优化问题时，不受连续可微的约束，而且具有并行处理能力，易于搜寻最优解。文献[8]指出遗传算法在解决运算规模较大的极值问题时具有良好效果，但是其算法同时具有早熟收敛的特性，需要对算法进行改进[8]。基于这种思想，笔者将极大熵与遗传算法结合，从而解决平衡机优化问题。

1 平衡机优化模型

用于防空武器发射装置中的平衡机通常有弹簧拉式、推式以及扭板式，笔者主要以弹簧推式平衡机为研究对象，其他类型平衡机的优化设计与此类似。弹簧推式平衡机的结构原理[9]如图1所示。

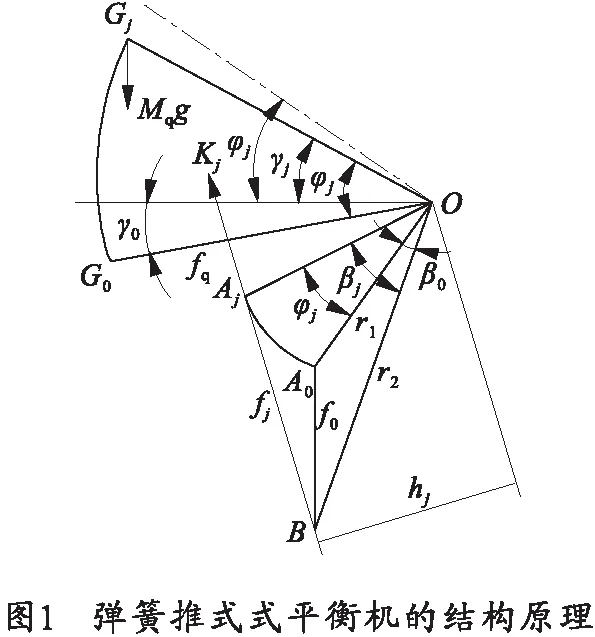
图1中，O为耳轴中心；A0是平衡机力对摇架的作用点(OA0=r1)；B是平衡机力对上架的作用点(OB=r2)；Gj、Mq分别为起落部分的质心与质量；γj是OGj与水平线的夹角；γ0是结构角；f是弹簧的压缩量；hj代表平衡机弹簧力对摇架的力臂；φj为射角；Kj是指一个平衡机的弹簧力。图中符号的下标0和j表示射角φ=0与任意射角φj时的状态。以下式中的下标m与l表示最大射角φmax与最小射角φmin时的状态。

1.1 不平衡力矩分析

由图中可以看出，随着射角φj的增大，弹簧的压缩行程随之变化，因此，可以通过几何关系确定平衡机力臂hj。

(1)

因此当φj=φmax时，有:

当φj=φmin时，有:

则当射角由φmax到φmin时，弹簧的压缩行程为:

λ=±(fm-fl)

(4)

令Mpj是射角为φj时，平衡机弹簧抗力Kj对耳轴的力矩，则有:

(5)

式中:c是弹簧的刚度系数;n是平衡机个数，对于一般的弹簧式平衡机，n一般取值为2。平衡机的预压力为Km，则对于弹簧推式平衡机有：

Kj=Km+c(fm-fj)

(6)

Mqj是起落部分重力矩，有:

(7)

根据平衡机的用途，设计时应以不平衡力矩最小作为评价设计方案优劣的标准。由式(1)～(8)可知，不平衡力矩为:

ΔMj=Mpj-Mqj=n[Km+c(fm-fj)]hj-

Mqgfqcosγj

(8)

1.2 优化参数的选择

在平衡机的设计过程中，影响平衡机性能的因素有很多种，因此其优化设计的因素也不止一种。结合平衡机的工作原理以及实际的工作过程，根据图1与式(1)～(8)可以得出以下几个结论：

1)平衡机的弹簧力矩与弹簧抗力Kj以及力臂hj成正相关关系，而且在已知平衡机个数的情况下，其弹簧力矩仅与这两个因素相关。

2)弹簧的抗力是与其弹簧总形变量，即弹簧的总压缩量正相关的，且与弹簧的刚度系数也是正相关的。弹簧的抗力仅受弹簧刚度系数c和弹簧的总压缩量fi的影响。

3)起落部分的重力矩是关于射角φ的余弦函数，且φ的角度范围一定且已知，在起落架质量确定的情况下，起落部分的重力矩仅与φ和结构角γ0相关。

在实际的安装过程中，结构角γ0通常较小，而且由于射角变化较大，结构角对于起落架重量力矩的影响较小，可以忽略。在设计的过程中，起落架质量Mq、臂长fq、平衡机个数n、结构角γ0、最大射角φmax和最小射角φmin是已知的。综合结论1)～3)可知，不平衡力矩ΔMj是参数r1、r2、β0、c、Km以及φj的函数。由于射角φ不对平衡机的性能产生影响，可以将它作为状态变量，因此平衡机的优化参数为平衡机对摇架的力臂r1、平衡机力对上架的力臂r2、初始夹角β0、弹簧刚度系数c和平衡机预压力Km。

因此，平衡机优化设计时，参与优化的参数，即设计变量X，可取为：

X=(r1,r2,β0,c,Km)T=(x1,x2,x3,x4,x5)T

1.3 目标函数的建立

根据平衡机优化设计的原则[10]，取其设计目标函数F(X)为:

并且求出使F(X)为最小的设计变量，作为平衡机的最优设计方案，即:

F(X*)=minF(X)

则平衡机的最优设计方案为:

式中：r1、r2和β0是确定平衡机位置的参数；c和Km是确定平衡机弹簧的参数。

2 算法设计

在对平衡机进行优化设计时，毛保全[9]、谈乐斌[10]等人在专著与论文中采用的方法通常是单纯形法和复合形法。实践证明单纯形法在解决线性规划问题时可以取得很好的效果，但是在解决非线性问题时并不能得到理想的结果[11]。复合形法是一种解决非线性问题时的有效算法，然而文献[12]指出：复合形法搜索路径长，迭代计算步骤多，效率较低。

在1.3节中得到的平衡机优化设计目标函数可以看出，平衡机优化问题属于极大极小值问题，也即minimax问题。minimax问题是数学规划中一类典型的非光滑优化问题，要求在极大的条件下求目标函数的极小值。由于目标函数包含极大项，所以它是连续但不可微的。因此在解决该类问题时，并不能直接用带导数的无约束优化算法来求解这种问题。这种问题可以描述为式(9)的形式:

(9)

其中，x=(x1,x2,…,xn)T∈Rn。

极大极小问题的研究有着重要的理论意义和实际价值。但由于目标函数不可微，给以梯度为基础的传统方法的求解带来了困难[13-15]。近年来，智能优化算法的兴起为求解此类问题提供了新的思路。基于这种思想，结合文献[16]，笔者利用极大熵法将问题转化为光滑函数，并采用改进遗传算法对问题进行求解。为解决传统遗传算法的缺陷，对算法进行了改进，以使得结果更为可靠。

3 模型的转化

3.1 问题的极大熵法转化

(10)

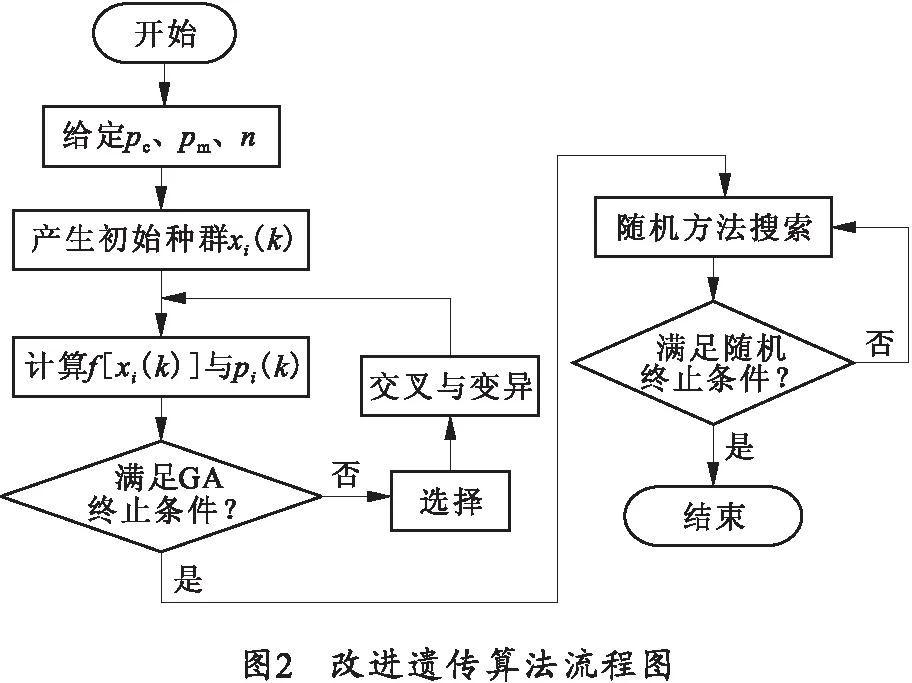
3.2 改进遗传算法

1)设定种群规模n=100，变异概率pm=0.1以及交叉概率pc=0.6，终止进化代数T=300。

2)染色体编码。采用浮点数编码，并用轮盘赌法产生初始群体。

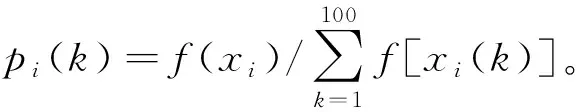
4)交叉变异。由于基本位变异发挥作用缓慢，效果不明显，参考文献[17]，笔者对遗传算法进行改进，采用三点交叉法来解决问题。

5)重复步骤3)、4)直到满足遗传算法的收敛条件。

6)结果的深层次优化。文献[18]指出：随机方向法的搜索运算是一种能保证迭代产生的点列为函数单调下降的良好局部极值数值优化算法。因此，经随机方向法的搜索运算产生的新的个体继承了其父代的优良品质，得到比标准遗传算法更优的结果。因此将步骤5)得到的最优个体作为随机方向法的初始点，做进一步优化，直到计算精度满足算法设定的终止条件。

改进的遗传算法流程图如图2所示。

4 优化结果分析

某防空武器系统的弹簧推式平衡机的设计参数中已知的数据为：γ0=0.92°,φmax=63.5°,φmin=-3°,Qq=990 kg,lq=553 mm,n=2。设计变量的取值范围如下：

150≤x1≤300,500≤x2≤700,3≤x3≤116.5,20≤x4≤40,200≤x5≤400

根据问题求解需要，将射角离散化，令:

将参数带入式(10)，采用本文第2节中的算法求解平衡机优化设计问题，运算50次，取50次计算的平均值，进行尺寸圆整后的优化结果如表1所示，遗传算法求解过程如图3所示。

表1中括号内为文献给出结果，也即优化计算结果。然而实际计算结果却和优化计算结果不同。造成这种现象的原因可能是文献[9]、[10]在优化求解时并未将优化结果带入原方程求解，将适应度函数值作为其最优解，从而产生了误差。

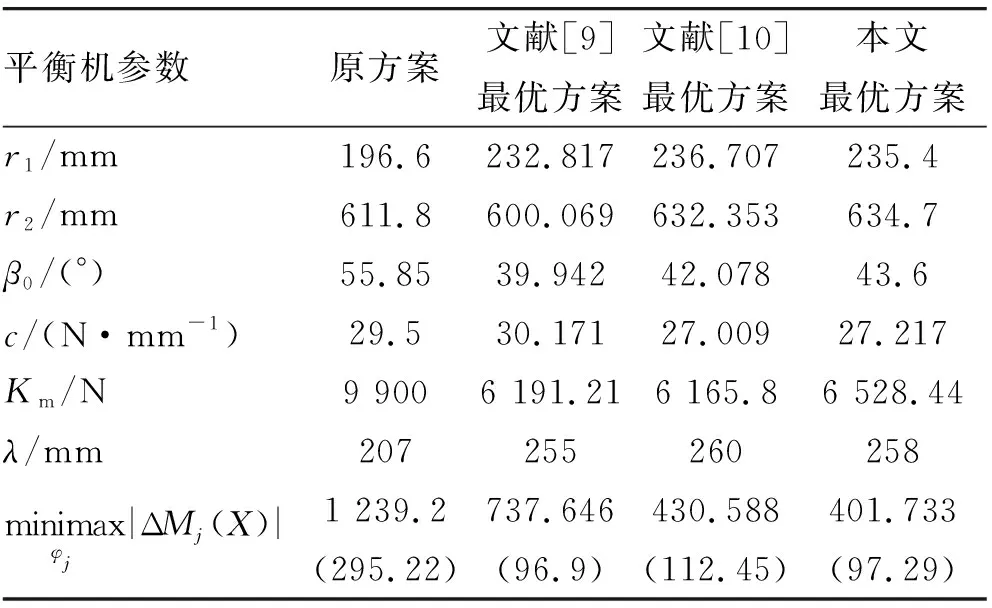
表1 平衡机优化设计方案对比表

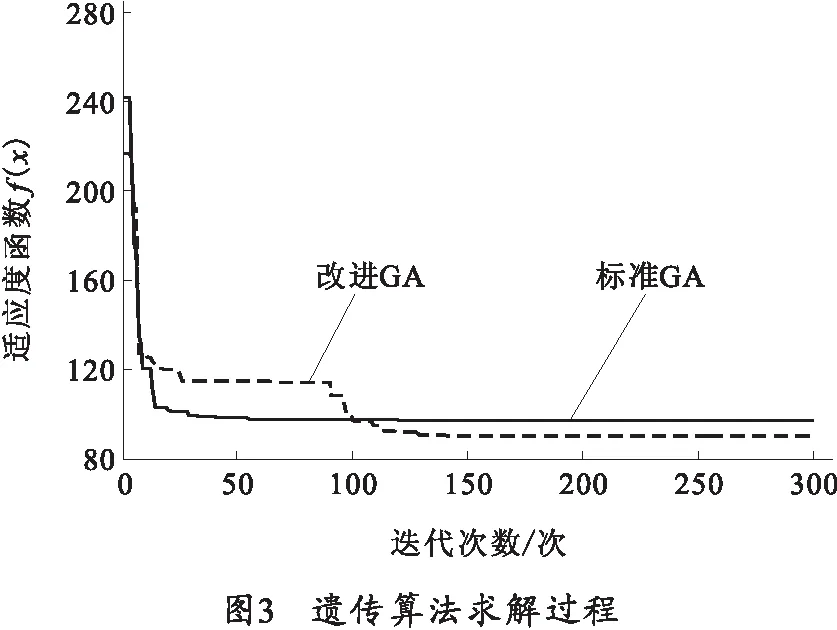
由表1可知，文献[9]、[10]分别利用单纯形法与复合形法对该武器的推式平衡机进行了优化，优化设计结果表明，最大不平衡力矩分别较原方案减少了41%、66%，优化结果较理想。采用本文的基于极大熵法和改进遗传算法的混合算法对该平衡机进行优化后发现，优化结果较文献[9]改进了45.6%，较文献[10]改进了6.8%。由图3的算法求解过程可以看出，利用本文改进遗传算法进行求解，收敛速度较慢，但利于寻找全局最优解，求解结果较标准遗传算法优。因此，本文采用的改进遗传算法在平衡机优化设计方面具有很好的效果。

5 结束语

在求解极大极小值问题时，极大熵法提供了一种行之有效的方法。通过极大熵法将非光滑的函数转化为光滑的极值问题，使得问题得到了简化。改进的遗传算法改善了传统遗传算法的早熟收敛问题，并通过随机方向法对优化结果进行搜索，使得问题的解尽可能逼近最优解，算法可靠性较高。通过对比发现，新算法优于当前平衡机优化设计中的常用算法。

[1] 谈乐斌,张莉芳,张月林.气压式平衡机的优化设计[J]. 火炮发射与控制学报, 1998(3):25-28.

TAN Le-bin, ZHANG Li-fang, ZHANG Yue-lin. Optimization design of air pressure balancing machine[J]. Journal of Gun Launch & Control, 1998(3):25-28. (in Chinese)

[2] D Applegate, W Cook, S Dash, et al. Solution of a min-max vehicle routing problem[J]. Informs Journal on Computer, 2002(14):132-143.

[3] E M Arkin, R Hassin, A Levin. Approximations for minimum and min-max vehicle routing problems[J]. Journal of Algorithms, 2006(59):1-18.

[4] Fusheng Wang, Yanping Wang. Nonmonotone algorithm for minimax optimization problems[J]. Applied Mathematics and Computation, 2011(217):6296-6308.

[5] A Cramer, S Sudhoff,E Zivi. Evolutionary algorithms for minimax problems in robust design[J]. Evolutionary Computation, IEEE Trans. 2009, 2(13):444-453.

[6] 薛毅.求解Minimax优化问题的SQP方法[J]. 系统科学与数学, 2002, 22(3):355-364.

XUE Yi. The SQP method for soving minimax problem[J]. Journal of Systems Science and Mathematical Sciences, 2002, 22(3):355-364.(in Chinese)

[7] Yu Xiao, Bo Yu. A truncated aggregate smoothing newton method for minimax problems[J]. Applied Mathematics and Computation, 2010 (216):1868-1879.

[8] 玄光男, 程润伟, 于歆杰,等. 遗传算法与工程优化[M]. 北京：清华大学出版社, 2004:101-120.

XUAN Guang-nan, CHENG Run-wei, YU Xin-jie. Genetic algorithms and engineering optimization[M]. Beijing: Tsinghua University Press, 2004:101-120. (in Chinese)

[9] 毛保全, 邵毅. 火炮自动武器优化设计[M]. 北京：国防工业出版社, 2007:153-187.

MAO Bao-quan, SHAO Yi. Optimization of gun automatic weapon[M]. Beijing: National Defense Industry Press, 2007:153-187. (in Chinese)

[10] 谈乐斌. 弹簧推式平衡机的优化设计[J]. 制造业自动化. 1999(8):14-17.

TAN Le-bin. Optimization design of spring push type balancer[J]. Manufacturing Automation,1999(8):14-17. (in Chinese)

[11] 王建群, 卢志华, 哈布哈琪. 求解约束非线性优化问题的群体复合形进化算法[J].河海大学学报, 2001, 3(5):46-50.

WANG Jian-qun, LU Zhi-hua, HA Bu-haqi. A group complex evolution algorithm for nonlinear constrained optimization problem[J]. Journal of Hehai University,2001, 3(5):46-50. (in Chinese)

[12] 雍龙泉, 孙培民, 张建科. 一类非线性极大极小问题的极大熵社会认知算法[J]. 计算机工程与应用, 2010, 46(26):36-37, 42.

YONG Long-quan, SUN Pei-min, ZHANG Jian-ke. Maximum entropy social cognitive optimization algorithm for a class of nonlinear minimax problems[J]. Computer Engineering and Application, 2010, 46(26):36-37,42. (in Chinese)

[13] Obasanjo E，Tzallas-Regas G，Rustem B. An interior-point algorithm for nonlinear minimax problems[J]. Journal of Optimization Theory and Applications, 2010, 144(2):291-318.

[14] Huyer W，Neumaier A. A new exact penalty function[J]. SIAM Journal on Optimization, 2003, 13(4): 1141-1158.

[15] Zhu Z. An improved SQP algorithm for solving minimax problems[J]. Applied Mathematics Letters, 2009, 22(4):464-469.

[16] 田益祥, 陈华富. 非线性极大极小问题的一个有效算法[J]. 电子科技大学学报. 2001, 30(3):316-319.

TIAN Yi-xiang, CHEN Hua-fu. An effective algorithm for nonlinear constraint max-min problems[J]. Journal of University of Electronic Science and Technology of China, 2001, 30(3):316-319. (in Chinese)

[17] 李应, 王琦, 王源博,等. 改进遗传算法及其在Matlab中的应用[J]. 机械工程师, 2011(11):42-43.

LI Ying, WANG Qi, WANG Yuan-bo, et al. Improved genetic algorithms and its application in Matlab[J]. Mechanical Engineer, 2011(11):42-43. (in chinese)

[18] 陈建涛, 蒋亚峰. 改进的粒子群算法在桁架结构优化设计中的应用[J]. 应用数学与计算数学学报. 2012, 26(4):449-453.

CHEN Jian-tao, JIANG Ya-feng. Application of improved particle swarm algorithm in truss structure optimization design[J]. Communication on Applied Mathematics and Computation. 2012, 26(4):449-453. (in Chinese)