一类平面二次系统(III)类方程的同宿分支问题

王宁宁，祝晓薇，张利群，丁本艳

(1.临沂大学 理学院，山东 临沂 276005;2.山东师范大学 数学科学学院，山东 济南 250014)

0 引言

著名数学家希尔伯特早在二十世纪初的国际数学家大会上提出了23 个著名数学问题，对20 世纪的数学发展起到了很大的推动作用. 其中，第16 个问题的后半部分为:多项式微分系统的极限环的最大个数是多少?相对位置如何?自那以后特别是近几十年来，数学工作者花费了大量的时间和精力致力于该问题的研究，取得了一系列卓越的研究结果.其中在对平面二次系统的研究中，著名数学家叶彦谦先生给出了如下的叶彦谦分类:

关于二次微分系统的极限环问题的研究，近几十年来已有大量的工作［1，2］.但是，通常采取的方法是作适当的变换把方程化为Liénard形式，再利用定性的方法来讨论极限环的存在性.文［6］利用分支的方法，通过分析未扰方程的同宿轨经扰动破裂以后的稳定流形和不稳定流形之间的相对距离，研究了一类含五个自由参数的平面二次微分系统(III)类方程的极限环的存在性问题.本文对文［6］中方程进行改进，并研究改进后一类含六个自由参数的平面二次微分系统(III)类方程的同宿环的分支问题，给出系统存在极限环的条件.

1 引理

首先给出几个引理.

考虑平面自治系统

及其扰动系统

引理1 (P －B 环域定理)［3］.设D是由两条不相交的单闭曲线Γ1和Γ2所围成的环域，并且系统在D内无奇点.如果当时间t增加时从Γ1和Γ2上出发的轨线都进入(都离开)D，那么在D内至少存在一个稳定(不稳定)的极限环.

注1.Γ1和Γ2可以部分地由轨线构成，甚至上面可以出现有限个奇点，只要保证轨线一旦进入(离开)D后不再离开(进入)即可.

注2.D的内边界(不妨设为Γ1)可以缩为一个不稳定(稳定)的奇点.

引理2［4，5］.假设1).系统(1)存在同宿于鞍点O(0，0)的同宿轨Γ，P0为Γ 上任意一点，过P0作(1)的横截线l与Γ 在P0点的外法线方向共线.

2).扰动系统(2)在O(0，0)点附近的鞍点为的稳定流形和不稳定流形与l的交点分别为Ps和Pu.则在小扰动下，从Ps到Pu的有向距离与同向时为正)为:

2 主要结果

我们有如下定理:

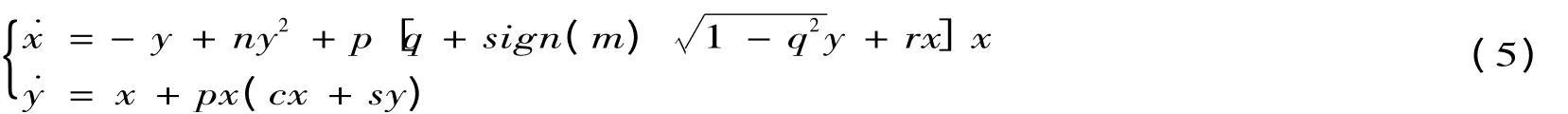
(1)当0＜δ＜2 时，系统(4)和(5)有鞍点不稳定焦点

(3)当－2＜δ＜0 时，系统(4)和(5)有鞍点，稳定焦点

(4)当δ ≤－2 时，系统(4)和(5)有鞍点，稳定结点

(1)当0＜ps ＜2 时，系统(6)有鞍点O(0，0)，不稳定焦点

(2)当ps≥2 时，系统(6)有鞍点O(0，0)，不稳定结点

(3)当－2＜ps ＜0 时，系统(6)有鞍点O(0，0)，稳定焦点

(4)当ps≤－2 时，系统(6)有鞍点O(0，0)，稳定结点

考虑系统(6)的未扰系统(6)p =0:

系统(7)有鞍点O(0，0)，中心且系统(7)为Hamilton 系统，其首次积分为:

当h =0 时，系统(8)为(7)过鞍点O(0，0)的同宿轨，记为Γ，即:Γ={u = u(t)，v = v(t)，t∈(－∞，+∞)}={(u，v):H(u，v)=0}，由系统(7)知Γ 为逆时针走向，经计算易知，Γ 与v轴的交点为不妨设此时t =0，即u(0)=0，v(0)= －

当n ＞0 时，系统(7)的同宿轨Γ 整体定义在v轴的负半平面，记其在v轴的右边部分为Γ+，在v轴左边部分为Γ－(当n ＜0 时，系统(7)的同宿轨Γ 整体定义在v轴的正半平面，记其在v轴的左边部分为Γ+，在v轴右边部分为Γ－)，由(8)知Γ+与Γ－的表达式分别为则:

下面利用P － B 环域定理证明极限环的存在性.要证Γ 内含有极限环，只需构造环域定理所需的内外境界即可.

(i)当δ＞0 时，为系统(6)的不稳定焦点(0＜δ＜2)或者不稳定结点

(ii)当δ＜0 时为系统(6)的稳定焦点(－2＜δ＜0)或者稳定结点(δ ≤－2).

定理证毕.

［1］叶彦谦.极限环论［M］.上海:上海科技出版社，1995.

［2］叶彦谦.多项式微分系统定性理论［M］.上海:上海科技出版社，1995.

［3］张芷芬，丁同仁.微分方程定性理论［M］.北京:科学出版社.1985.

［4］张锦炎，冯贝叶.微分方程几何理论和分支问题［M］.北京:北京大学出版社，2000.

［5］韩茂安，朱德明.微分方程分支理论［M］.北京:煤炭工业出版社，1994.

［6］朱曼，杨锁玲.郭丽艳.一类平面二次系统(III)类方程的极限环存在性［J］.枣庄学院学报，2012，29(2):42 －46.