Elman神经网络与ARIMA模型对流感发病率预测效果的比较*

孙锦峰, 耿云亮, 郭奕瑞, 王高帅, 高飞飞, 刘晓田, 尤爱国, 王重建#

1)郑州大学公共卫生学院社会医学与卫生事业管理学教研室 郑州 450001 2)郑州大学公共卫生学院流行病学教研室 郑州 450001 3)河南省疾病预防控制中心传染病所 郑州 450016

传染病的暴发流行是人类面临的重要的公共卫生问题，而基于理论流行病学的发病率预测对传染病防治工作的有效开展具有重要的指导意义[1]。流感是由流感病毒引起的一种严重威胁人类生命健康的急性呼吸道传染病，因具有传染性强、波及范围广、社会危害大等特点而受到特别的重视，尤其是近年来禽流感在局部地区的暴发流行[2-3]。Elman神经网络作为一种典型的非线性动态神经网络，在BP神经网络的基础上，通过延迟储存反馈输入状态而具有较强的动态学习能力，被广泛地应用到信号检测、交通流量预测等领域[4-6]。该研究利用河南省2006年1月至2011年12月的流感疫情监测资料建立基于Elman神经网络的流感发病率预测模型，通过与自回归移动平均(autoregressive integrated moving average, ARIMA)模型的比较，评价Elman神经网络模型的预测效能，探讨预测流感发病率的新方法。

1 资料与方法

1.1资料来源疫情数据源于国家疾病监测信息报告管理系统河南省2006年1月至2011年12月流感疫情监测资料，相关人口数据源于第六次全国人口普查报告。

1.2研究内容分别采用时间序列分析法和Elman神经网络理论对资料进行分析，建立基于流感发病率的最优ARIMA模型和Elman神经网络预测模型，通过实证研究评价不同模型的预测效能。

1.3研究方法

1.3.1 时间序列分析法 采用Box-Jenkins建模方法，ARIMA模型是其中最重要而又基本的模型之一。ARIMA建模一般分3个步骤：模型识别、参数估计、模型诊断和预测，通过对3个步骤的反复进行，筛选出最优预测模型。在ARIMA模型中，变量的未来取值可以表达为过去若干个取值和随机误差的线性函数，相关原理与公式详见文献[1，7]。

1.3.2 Elman神经网络 Elman神经网络作为经典的非线性动态网络，其网络结构可以分为4层：输入层、隐含层(中间层)、承接层和输出层。其中，输入层的单元仅起信号传输的作用；输出层单元起线性加权作用；隐含层单元的传递函数可采用线性或非线性函数；承接层又称为上下文层或是状态层，用来记忆隐含层单元前一时刻的输出层并返回给网络的输入，可以认为是一个一步延时算子。相关原理与计算公式详见文献[4,6,8]。

1.3.3 不同模型预测效能的检验与评价 采用平均误差绝对值(mean absolute error,MAE)、平均误差绝对率(mean error rate,MER)和非线性相关系数(nonlinear correlation coefficient,RNL) 3个指标评价模型的预测效能，MER越小且RNL越接近1，表明模型的预测效果越好。具体公式如下:

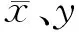
1.4统计分析利用Excel 2007对河南省流感疫情资料进行整理。采用SAS 9.1对流感不同年份发病率进行趋势χ2检验，建立ARIMA模型；通过Matlab 7.11软件实现Elman神经网络预测模型的建立、检验与评价。建模时根据河南省2006年1月至2011年12月的月流感发病率情况，选取2006年1月至2010年12月的数据作为训练集，选取2011年1月至12月的数据作为检验集。

2 结果

2.1流感发病率变化趋势2006年至2011年河南省共报告流感患者29 017例，年平均发病率为16.67%，其中2009年和2011年流感患者最多，共15 360例，占患病总数的53.22%，提示河南省在2009年和2011年发生过流感暴发流行。进一步分析发现，该省2006至2011年不同年份流感发病率(3.39/10万，2.99/10万，3.85/10万，9.61/10万，6.72/10万，4.29/10万)间的差异有统计学意义(P<0.01)，且各年间的发病率呈逐年上升的趋势(Z=42.572,P<0.001)。

2.2ARIMA模型通过对原始流感发病率序列的反复检验、模型识别、参数估计和模型诊断后，发现原始数据呈现出观察序列的平稳性(即d=0)，得到的相关ACF图(图1)呈现出拖尾性(此处为研究方便，限制q的取值范围为1～4)，偏相关PACF图(图2)呈现出1阶截尾(即p=1)，依据p、q的取值范围(p=0.1、2，q=0.1、2、3、4)分别建立15个ARIMA模型，以最小信息准则为参考标准来选取p、q值，确定p=1,q=0时为最优ARIMA(p,0,q)预测模型，结果详见表1，此时BIC(1,0)值最小，为-2.476 57，故ARIMA(1,0,0)模型为最优预测模型。该最优模型的预测结果显示：评估均值=0.434 236，差分阶数=0，自回归系数(autoregressive factors，Factor1)=1-0.558 01B**(1)，故该ARIMA(1, 0, 0)模型的预测公式为：

2.3Elman神经网络预测模型由于流感的发病率以年或季度为周期进行播报，故该研究选取4和1个神经元分别作为Elman神经网络的输入层节点和输出层节点；隐含层节点数的确定一般没有特定的要求，该研究利用原始的疫情资料，分别建立21(可调)个不同隐含层节点数的Elman神经网络模型(表2)，以误差0.000 01作为网络的训练目标，1 000作为网络的训练步数，通过比较模拟仿真结果的平均均方误差(MSE)，选取具有最小MSE的网络模型作为最优预测模型。可以看出，表2中以隐含层节点数为12的第10号Elman神经网络预测模型的MSE最小，并且该预测模型的隐含层节点数仅为12个，其模型的复杂性相对较低，不容易出现过度拟合的现象，进而减少了噪声的产生，故该研究采用的最优Elman神经网络预测模型的结构为4-12-1-1。

图1 原始观察序列的ACF图

图2 原始观察序列的PACF图

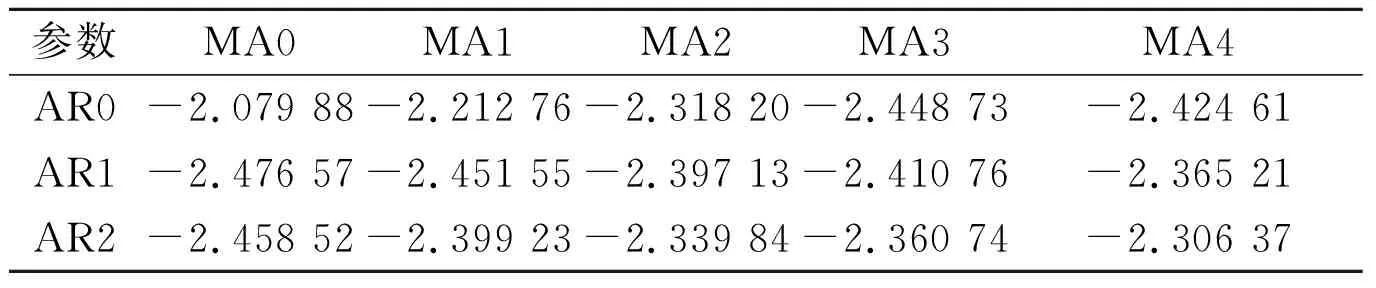
表1ARIMA(p,0,q)模型在p=0、1、2，q=0、1、2、3、4时的BIC值

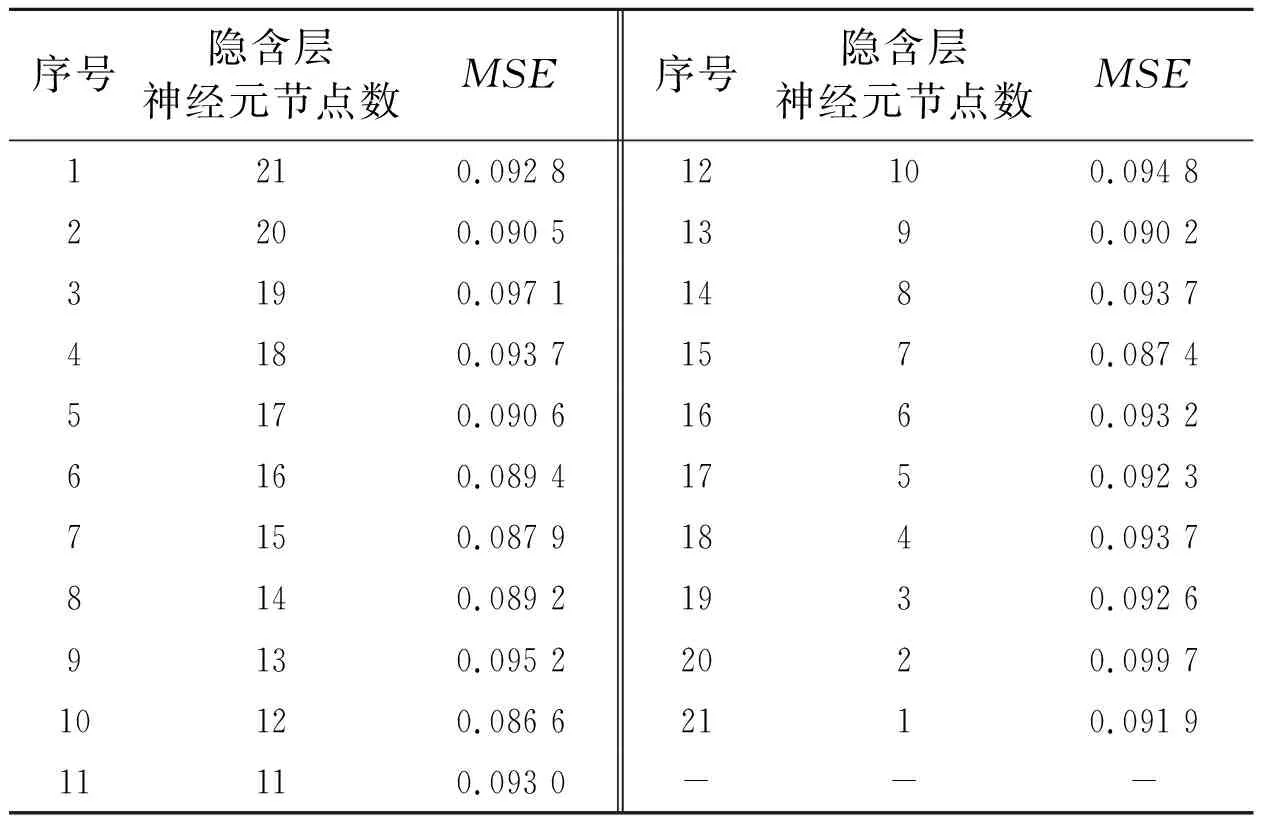
表2 不同隐含层节点数Elman神经网络预测模型的评估

2.4最优ARIMA(1,0,0)和Elman神经网络模型预测效能的检验与评估结果见表3。

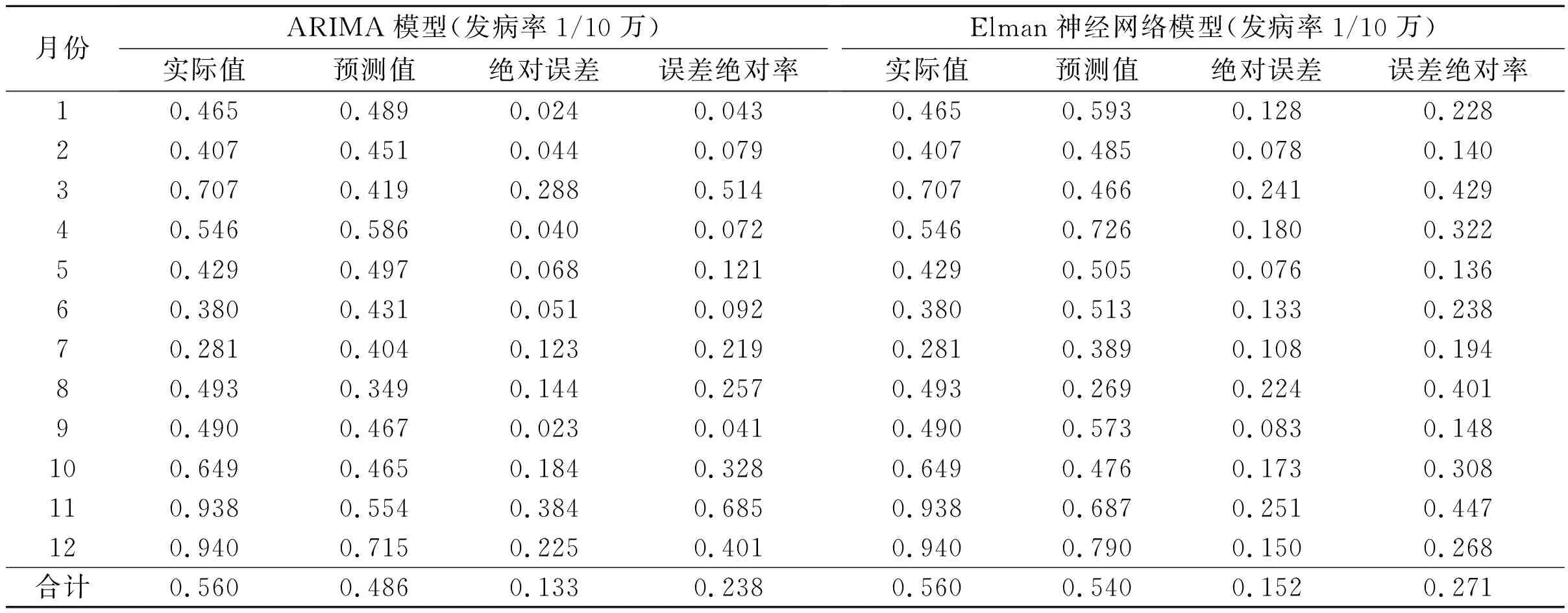
表3 最优ARIMA(1,0,0)和Elman神经网络模型预测效果比较

ARIMA(1,0,0)模型和Elman神经网络模型的MAE、MER以及RNL分别为0.133、0.238、0.708和0.152、0.271和0.725；可以看出与传统的ARIMA模型相比，Elman神经网络模型的预测效能并未有较高的提升(ΔMAE=-0.019,ΔMER=-0.033)，但非线性拟合能力却得到提升(即ΔRNL=0.017)。整体而言，两种最优模型的预测效能相近，且均能在一定程度上较佳地实现对流感发病率的拟合与预测。

3 讨论

传染病的暴发流行受到多种不确定因素的影响，这使得在传染病早期的预测预警上存在着诸多的困难，导致了传染病早期预防控制工作一直较为滞后，因此如何及时有效地预测预警传染病的暴发流行一直是传染病预测控制工作的重点[7,9]。尽管到目前为止，已有诸多的数学模型运用到传染病的预测预警当中，特别是线性模型如控制图法、时间序列模型、灰色模型、马尔科夫连模型等，但当在预测处于变化中的传染病疫情时，由于受到各种人为因素的干扰，疫情数据呈现出较大的波动，降低了其反映真实暴发流行情况的能力，进一步使模型的预测效能降低[10]。

该研究在时间序列分析和Elman神经网络的理论基础上，利用河南省2006年1月至2011年12月的流感疫情资料，建立ARIMA(1,0,0)模型和Elman神经网络模型。实证研究显示，两种最优预测模型的预测结果均与实际发病率趋势相一致，且两种模型的预测效能相近，均能较好地预测河南省2011年流感发病率。进一步分析显示，Elman神经网络预测模型的预测值的平均误差(ΔME=0.020)较ARIMA(1,0,0)模型(ΔME=0.074)小，且RNL较ARIMA(1,0,0)高(ΔRNL=0.017)，但是MAE和MER均较ARIMA(1,0,0)模型大(ΔMAE=-0.019、ΔMER=-0.033)，提示与线性ARIMA(1,0,0)模型相比，Elman神经网络模型的非线性拟合能力较强，能使预测值均匀地分布在实际值的两侧，减弱了人为或其他干扰因素对疫情数据造成的剧烈波动，一定程度上更为真实地反映了流感暴发流行的实际情况。

此外，Elman神经网络预测模型在实际应用中存在一定的滞后性，其主要原因可能有以下几点：①该研究在充分挖掘既往流感发病率疫情数据的同时，忽略了流感在暴发流行过程中所受到自然因素、社会因素等诸多因素的影响。②该模型只是充分利用了在流感暴发流行过程中人为因素所产生的直接效应，此种效应主要体现在人为干预后所引起的流感发病率的暂时性下降上，并没有全面地反映出人为干扰因素所产生的全部效应。③Elman神经网络作为一种典型的动态神经网络，其本身具有较强的容错特性，此种固有的特性不可避免地会对模型自身的预测效能产生影响。

总之，Elman神经网络模型与其他常用的预测方法一样，作为一种数据处理方法，主要从数据上反映疾病的发展变化趋势。此外，实际工作中，有很多影响流感发病的因素未被考虑到模型的参数中，从而影响到结果的准确性。因此，在制定流感的预防控制策略和具体的措施时还必须考虑其他综合因素对预测结果的影响。

[1]刘刚, 唐宋, 孙文杰. 时间序列分析法在香港结核病预测中的应用[J]. 中国卫生统计，2012, 29(2): 226

[2]王重建, 于二曼, 余宏杰, 等. 甲型H1N1流感不同流行时期农民知信行变化趋势分析[J]. 现代预防医学，2012,39 (6): 1525

[3]郭永豪, 张明瑜, 蒋红丽, 等. 郑州市人群甲型H1N1流感病毒感染趋势和抗体水平分布[J]. 郑州大学学报:医学版, 2011,46(2):256

[4]赵建玉, 高慧, 贾磊. 基于Elman神经网络的短时交通流预测模型[C]. 昆明:第二十七届中国控制会议论文集，2008:499

[5]罗勇, 郑金, 宁美凤. 短期电力负荷组合预测方法研究[J]. 郑州大学学报:工学版, 2013,34(1):78

[6]Szkola J, Pancerz K, Warchol J. Recurrent neural networks in computer-based clinical decision support for laryngopathies: an experimental study[J]. Comput Intell Neurosci，2011,2011: 289398 doi:10.1155/2011/289398

[7]杨召, 叶中辉, 尤爱国, 等. 乘积季节ARIMA模型在结核病发病率预测中的应用[J]. 中国公共卫生, 2013,29(4): 469

[8]Song Q. On the weight convergence of Elman networks[J]. IEEE Trans Neural Netw, 2010,21(3): 463

[9]赖圣杰, 李中杰, 金连梅, 等. 传染病暴发早期预警系统评价内容及其指标[J]. 中华流行病学杂志, 2009,30(6): 637

[10]王丙刚, 曲波, 郭海强, 等. 传染病预测的数学模型研究[J]. 中国卫生统计, 2007,24(5): 536