E-稠密半群上的最小群同余
2013-11-19杨燕
杨 燕
(商洛学院 数学与计算科学系,陕西商洛 726000)
设S是半群,用E(S)表示S的幂等元集合,Reg(S)表示S的正则元集合。称S为E-反演半群,如果S中的每一个元素a,存在x∈S,使得ax∈E(S)。半群S称为E-半群,如果E(S)形成S的一个子半群。近年来人们对E-反演E-半群,即幂等元形成子半群的E-反演半群的研究非常热衷,Weipoltshammer[1-2]研究了E-反演E-半群的一些基本性质和其上的几类特殊同余;Srinivas[3]给出了E-反演E-半群的若干等价刻画;Siripitukdet等[4-5]对E-反演E-半群的最大幂等元分离同余和带同余进行了研究。半群S称为E-稠密半群[6],如果S是E-反演半群且幂等元相乘可交换。事实上,在E-稠密半群S中E(S)是半格。在文献[7]中已经研究了E-稠密半群的局部化,证明了E-稠密半群的局部化同构于其最大群同态象,本文主要利用E-稠密半群局部化的结论,给出了E-稠密半群上的最小群同余的一个表示及若干等价刻画,从而极大地丰富了E-稠密半群上的最小群同余的刻画,在对强π-逆半群[8]和逆半群[9]上一些结果进行推广的同时,也获得了强π-逆半群和逆半群上最小群同余的一些新的结论。文中未加以定义的概念和记号,见文献[9-10]。
设S是半群,对任意a∈S,若存在x∈S,使得x=xax,则称x是a的弱逆元,简称弱逆。用W(a)表示a的所有弱逆的集合,即W(a)={x∈S|x=xax}。由文献[11]知,半群S是E-反演半群当且仅当S中的每个元素至少有一个弱逆元,即对任意的a∈S,W(a)≠Ø。
半群S上的同余σ称为S上的最小群同余,如果S/σ是群,且对于S的任意群同余ρ,有σ⊆ρ。这时,S/σ 是 S 的最大群同态象[8];反之,如果S′是S的最大群同态象,则同态核就是S的最小群同余。
1 引理
引理1[2]设S是E-半群,则
i)对任意 a∈S,a′∈W(a),e,f∈E(S),有 ea′,a′f,ea′f∈W(a);
ii)对任意 a∈S,a′∈W(a),e∈E(S),有a′ea,aea′∈E(S);
iii)对任意 e∈E(S),有 W(e)⊆E(S);
iv)对任意 e,f∈E(S),有 W(ef)=W(fe)。
引理2[7]设S是E-稠密半群,则S在幂等元半格E(S)上的局部化S[E(S)-1]是S的最大群同态象。
注:S[E(S)-1]=(S×E(S))/~={a/e|a/e 表示(a,e)所在的等价类,其中取定 e∈E(S),∀a∈S}。
2 定理及其证明
定理1 设S是E-稠密半群,E(S)为S的幂等元半格,则二元关系
σ={(a,b)∈S×S|(∃f∈E(S))af=bf}是S上的最小群同余。
定理1的证明 由引理2的注知S[E(S)-1]关于同态 λ:S→S[E(S)-1],a|→a/e 是 E-稠密半群 S的最大群同态象,则λ的核就是S的最小群同余,λ的核为
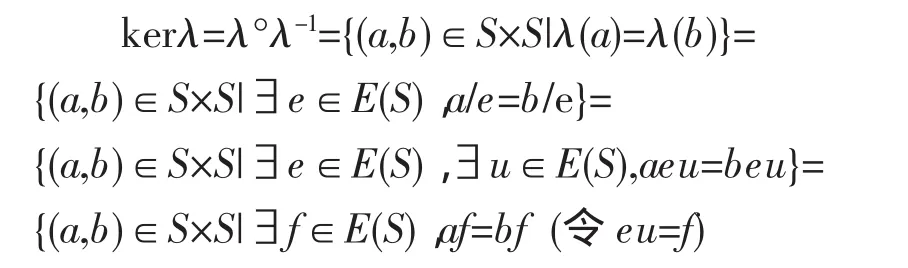
所以 σ={(a,b)∈S×S|(∃f∈E(S))af=bf}是 S 上的最小群同余。
定理2给出了E-稠密半群S上的最小群同余的10条等价刻画。
定理2 设S是E-稠密半群,σ是S上的最小群同余(σ的定义见定理1),则对任意的a,b∈S,下列各款等价
1)aσb;
2)(∃e∈E(S))ea=eb;
3)(∃e,f∈E(S))ea=fb;
4)(∃e,f∈E(S))ae=bf;
5)(∃e∈E(S))eae=ebe;
6)(∃x∈Reg(S))xa=xb;
7)(∃x∈Reg(S))ax=bx;
8)(∀e,f∈E(S))(∃g∈E(S))aeg=bfg;
9)(∀e,f∈E(S))(∃g∈E(S))gea=gfb;
10)(∀e,f∈E(S))(∃x∈Reg(S))aex=bfx;
11)(∀e,f∈E(S))(∃x∈Reg(S))xea=xfb。
定理 2 的证明 1)⇒2)设 aσb,则存在 f∈E(S),使得 af=bf。设 a′∈W(a),b′∈W(b),由引理 1 的 ii)知 afa′,bfb′∈E(S),又 S中幂等元相乘可换,则有
bfb′afa′·a=bfb′·bf·a′a=bf·a′a·b′bf=af·a′a·b′bf=afa′·af·b′b=afa′·bf·b′b=bfb′afa′·b
由于 E(S)是 S 的子半群,所以 bfb′afa′∈E(S)。令 e=bfb′afa′,则有 ea=eb。
2)⇒3)显然成立。(只需令f=e即可)
3)⇒4)设存在e,f∈E(S),使得 ea=fb。对a′∈W(a),b′∈W(b),有 b′fb,a′ea∈E(S)。由于幂等元相乘可换,则有
a·a′eab′fb=aa′·fb·b′fb=aa′·bb′·ffb=aa′·bb′·fb=bb′·aa′·fb=bb′·aa′fb=b·b′aa′fb。
由于 E(S)是 S的子半群,所以 a′eab′fb∈E(S),aa′f∈E(S),由引理 1 的 ii)知 b′aa′fb∈E(S),令g=a′eab′fb,h=b′aa′fb,则 ag=bh。
4)⇒1)设存在 e,f∈E(S),使得 ea=bf。S中幂等元相乘可换,则有
a·ef=aeef=bfef=beff=b·ef
又 E(S)是子半群,所以 ef∈E(S),令 g=ef,则 ag=bg。
故 1),2),3),4)等价。
2)⇒5)设存在 e∈E(S),使得 ea=eb。给等式两端同时乘以e,得eae=ebe。
5)⇒2)设存在 e∈E(S),使得 eae=ebe。设a′∈W(a),b′∈W(b),给等式两端同时乘以 bb′aa′,得
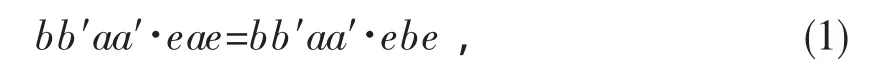
根据 S中幂等元相乘可换以及 bb′,aa′,aea′,a′ea,beb′,b′eb 都是 S 的幂等元,等式(1)变为

给等式(2)两端同时乘以 aa′·bb′·e·aea′·b′eb,并令此幂等元为f,有
左端=aa′·bb′·e·aea′·beb′·bb′·aea′·e·a=aa′·bb′bb′·ee·aea′aea′·beb′·a=aa′·bb′·e·aea′·beb′·a=fa
右端=aa′·bb′·e·aea′·beb′·aa′·beb′·e·b=aa′aa′·bb′·ee·aea′·beb′beb′·b=aa′·bb′·e·aea′·beb′·b=fb
即 fa=fb,故 5)与 2)等价
2)⇒6)设存在 e∈E(S),使得 ea=eb。由于E(S)⊆Reg(S),故 6)成立。
6)⇒2)设存在 x∈Reg(S),使得 xa=xb。取 x′∈V(x),则 x′x∈E(S),且 x′xa=x′xb,故 6)与2)等价。
类似可证7)与1)等价。
1)⇒8)设存在 e∈E(S),使得 ae=be。对任意的h,f∈E(S),由于 E(S)是半格,令 efh=g,则 g∈E(S),且ahg=ah·efh=aefh2=befh=bef2h=bf·efh=bfg。
8)⇒1)设对任意的 e,f∈E(S),存在 g∈E(S),使得aeg=bfg。给此式两端同时乘以fe,得aeg·fe=bfg·fe。由于S中幂等元相乘可交换,于是该式变为a·egf=b·egf,其中 egf∈E(S),故 8)与 1)等价。
类似可证9)与2)等价。
10)⇒8)设对任意的 e,f∈E(S),存在 x∈Reg(S),使得 aex=bfx。取 x′∈V(x),则 xx′∈E(S),且 ae·xx′=aex·x′=bfx·x′=bf·xx′,即 8)得证。
8)⇒10)由于 E(S)⊆Reg(S),故结论 10)显然成立。
故10)与8)等价。类似可证11)与9)等价。
综上,1)至 11)各款等价,证毕。
注记 作为定理2的推论,当S是强π-逆半群和逆半群时,由于这两类半群都是E-稠密半群,所以定理2中的每一条也都是强π-逆半群和逆半群上的最小群同余的表示刻画,但是需要注意的是,由于逆半群是正则半群,所以在逆半群中Reg(S)=S。
[1]Weipoltshammer B.On classes of E-inversive semigroups and semigroups whose idempotents form a subsemigroup[J].Commun Algebra,2004,32(8):2929-2948.
[2]Weipoltshammer B.Certain congruences on E-inversive E-semigroups[J].Semigroup Forum,2002,65(2):233-248.
[3]Srinivas K V R.Characterizations of E-semigroups[J].Southeast Asian Bull Math,2007,31(5):979-984.
[4]Siripitukdet M,Sattayaporn S.The maximum idempotent separating congruence on E-inversive E-semigroups[J].International Journal of Algebra,2008,2(19):925-931.
[5]Siripitukdet M,Sattayaporn S.Band congruence on E-inversive E-semigroups[J].International Journal of Algebra,2010,4(19):925-931.
[6]Margolis S W,Pin J E.Inversive semigroups and extensions of groups by semilattices[J].JAlgebra,1987,110(2):277-297.
[7]杨 燕.E-稠密半群的局部化[J].商洛学院学报,2012,26(6):14-16.
[8]高理平.强π-逆半群的局部化与最小群同余[J].数学研究,1997,30(2):193-198.
[9]Hoiwe J M.Fundamentals of semigroup theory[M].Oxford:Clarendon Press,1995.
[10]Bogdanowic S.Semigroups with asystem of subse migroups[M].Yogoslavia:Novysad,1985.
[11]Mitsch H,Petrich M.Basic properties of E-inversive semigroups[J].Commun,in Algebra,2000,28(11):5169-5182.
