矩阵环的欧拉恒等式

曹明,冯怡君,魏亚萍,游松发

(湖北大学数学与计算机科学学院,湖北 武汉 430062)

0 预备知识

一个有限连通有向图Γ称作欧拉图,当且仅当Γ满足下列条件之一:

1)∀i∈A,φ(i)=0

2)∃p,q∈A,使φ(p)=1,φ(q)=-1,且∀i∈A<[p,q},φ(i)=0

Swan定理[1]若欧拉图Γ有V个顶点,E条边,且E≥2V,则Π(Γ)中奇偶置换各半.

构造1用欧拉图构作多重线性多项式.

令Γ是有N条边e1,e2,…,eN的欧拉图,利用Π(Γ)及E={e1,…,eN}所对应的非交换未定元集X={x1,…,xN},我们可以构作与Γ相应的多重线性多项式

构造2用矩阵单位替换映射和欧拉图构作新的有向图.

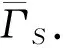
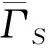
构造3利用欧拉路构造只有唯一欧拉路的欧拉图.

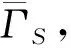
首先,我们定义函数π*:{1,2,…,N+1}→A={1,2,…,k},使π*(1)=σ(eπ(1));π*(r)=σ(eπ(r))=τ(eπ(r-1)),2≤r≤N,π*(N+1)=τ(eπ(N)).

然后,按递归的方式来定义二元序列:(g(1),w1),(g(2),w2),…,(g(r),wr)(1≤r≤N+1),其中g(r)是自然数,wr⊆{1,2,…,N,N+1}.

若令g(1)=1,w1=Φ,须考虑3种情形:

情形1．π*(r+1)≠π*(t),∀1≤t≤r;

情形2．π*(r+1)=π*(t),π*(r+1)≠π*(s),∀t+1≤s≤r,t∈wr;

情形3．π*(r+1)=π*(t),π*(r+1)≠π*(s),∀t+1≤s≤r,t∉wr.

按以上3种情形,令

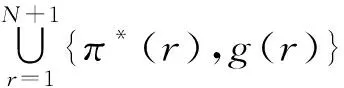
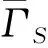
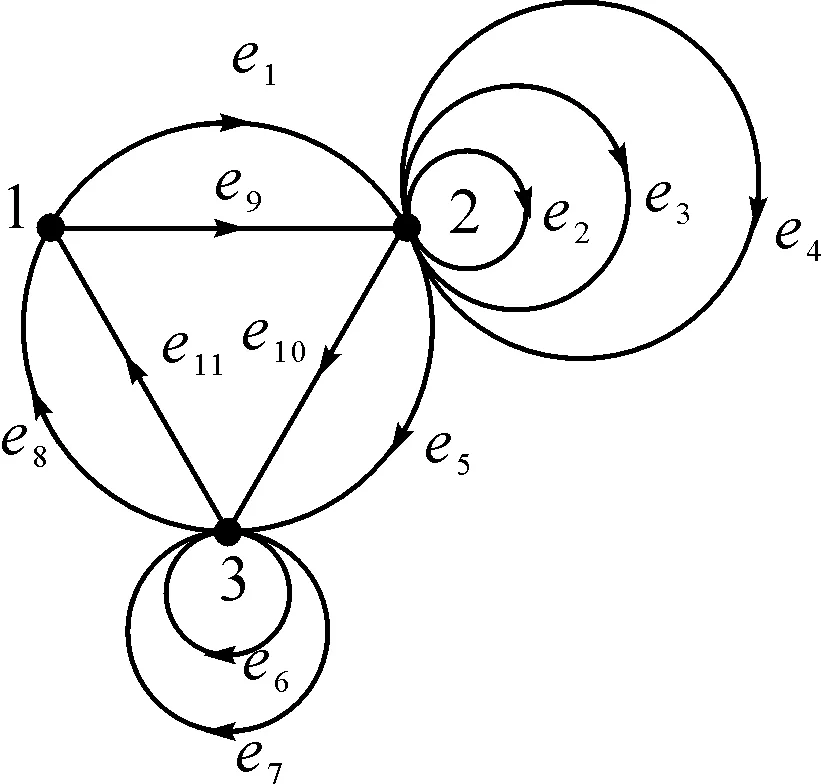
图1 欧拉图Γ

图2 欧拉图

1 主要结果

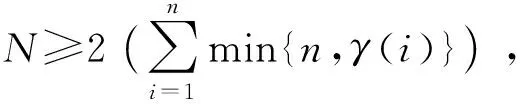
定理1的证明由于fΓ(X)是多重线性的,又C是交换环,只须证明对任意替换S:X={x1,…,xN}→{Eab|1≤a,b≤n},有fΓ(S(X))=0.

令S(xr)=Ea(r)b(r)(1≤r≤N),则

(1)

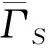
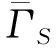
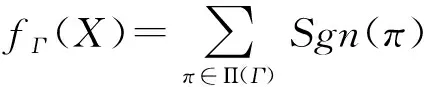
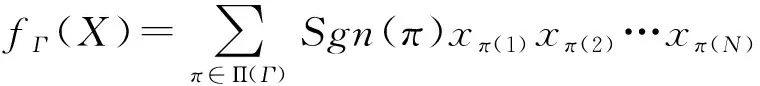
由(1)式,我们有n×n阵fΓ(S(X))在(g(1),g(N+1))位置上的元为Sgn(π),因而非零.

2 应用

图3 1个顶点、N条边的欧拉图

g(1)=g(2)=1

g(3)=g(4)=2

⋮

g(2s+1)=g(2s+2)=s+1

⋮

因而,对所有π∈Sym(N),有g(π)=[N/2]+1

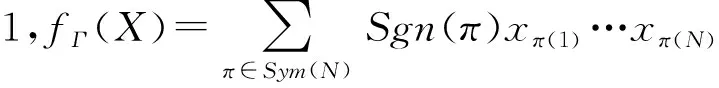
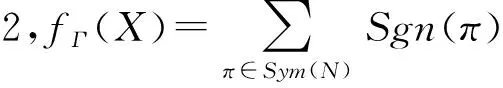
特别地,有

图4 kM条边的欧拉图

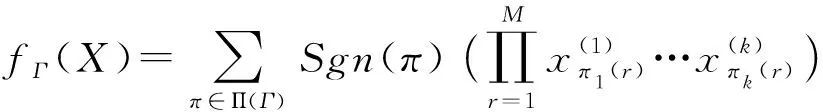
且易知,∀π∈Π(Γ),

g(1)=g(2)=…=g(k+1)=1,

g(k+2)=g(k+3)=…=g(2k+2)=2,

⋮

g(s(k+1)+1)=g(s(k+1)+2)=…=g((s+1)(k+1)=s+1,

⋮

因而对所有π∈Π(Γ),我们有g(π)=M-[(M-1)/(k+1)].

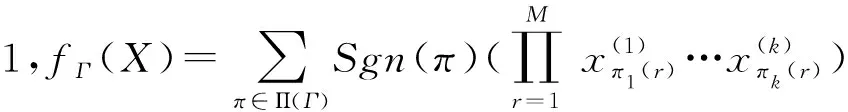
特别地,若k=2,M=2n,则Γ是有2个顶点,N=4n条边的欧拉图(如图5),若令π=π1×π2∈Sym(2n)×Sym(2n)=Π(Γ),记从1到2的边对应的未定元为:x1,…,x2n,从2到1的边对应的未定元为y1,…,y2n,我们有

图5 2个顶点、N=4n条边的欧拉图

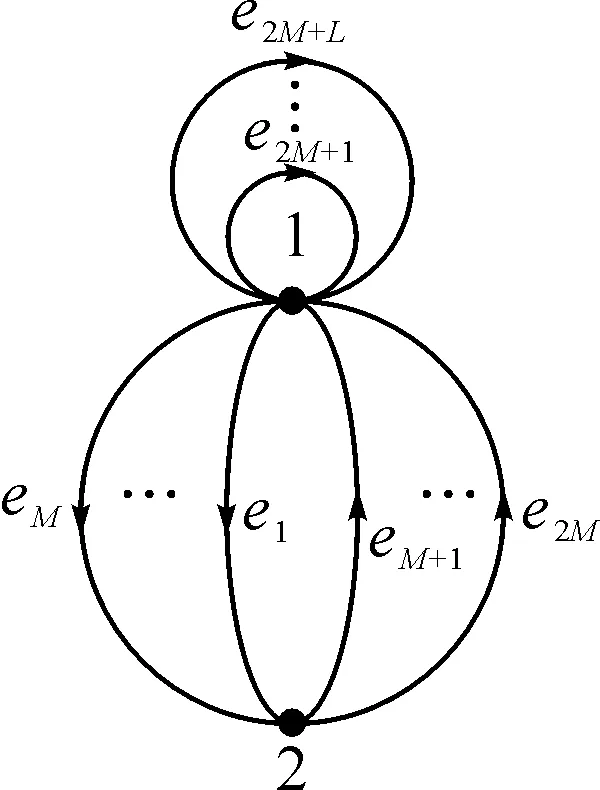
图6 2个顶点、L+2M条边的欧拉图

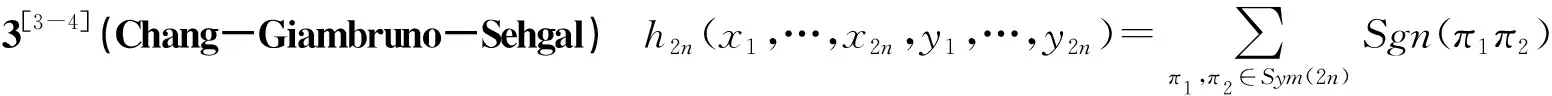
2)文献[3]中通过构造Mn(C)中双楼梯:x1=E11,y1=E12,x2=E22,y2=E23,…,xn=Enn,yn=Enn,xn+1=En,n-1,yn+1=En-1,n-1,…,x2n-1=E21,y2n-1=E11,得到h2n-1(E11,…,Enn,En,n-1,…,E21,E12,…,Enn,En-1,n-1,…,E11)=ΣEii≠0,

即h2n是Mn(C)的最小2-重Capelli多项式,但此时n≥g(π)=M-[(M-1)/(k+1)]=2n-[(2n-1)/3]并不成立,这一事实说明,定理2中n≥g(π)并不是fΓ(X)在Mn(C)上赋值非零的必要条件.

应用3若Γ是有两个顶点,L+2M条边的欧拉图(如图6),两顶点间的边数:α(1,1)=L,α(1,2)=α(2,1)=M,α(2,2)=0,若1到2,2到1,1到1的边分别对应的未定元集为X,Y,Z,我们有

定理3若C是有1的交换环,且对非负整数s,有sC≠{0},则fΓ(X,Y,Z)是Mn(C)的多项式恒等式,当且仅当

2M+L≥2(min{n,M+L}+min{n,M})

(2)

定理3的证明充分性是定理1的直接推论,

必要性,须考虑两种情形:

1)若M≤L/2,此时(2)式等价于n≤L/2;

若n>L/2,显然n≥[L/2]+1>M,考虑替换S:

S(xr)=E[L/2]+1,r,S(yr)=Er,[M/2]+1(1≤r≤M)

图7 M≤L/2时的欧拉图

若L为奇,图7中虚线出现,这条边可以出现在“花瓣”中任何地方,所有欧拉路在fΓ(S(X),S(Y),S(Z))中符号仍一致,只不过与L为偶时的情形相反而已.

我们得到n×n矩阵fΓ(S(X),S(Y),S(Z))中(1,[L/2]+1)位置的元非零.

2)M>L/2时(即M≥[L/2]+1),(2)式等价于n≤(M/2)+(L/4),

若n>(M/2)+(L/4),我们有n≥[L/2]+[(M-[L/2])/2]+1.

考察替换S:

S(xr)=E[L/2]+1,r,S(yr)=Er,[L/2]+1(1≤r≤[L/2]+1),

图8 M>L/2时的欧拉图

按(1)一样的方法可知n×n矩阵fΓ(S(X),S(Y),S(Z))在(1,[L/2]+[(M-[L/2])/2]+1)或(1,[L/2]+[(M-[L/2]-1)/2]+1)处(依赖于M-[L/2]的奇偶性)位置的元非零.

注:若M=0,我们可以得到Amitsur-Levitzki定理;若L=0,我们可以得到Chang-Giambruno-Sehgal定理.

[1] Swan R G. An application of graph theory to algebra[J]. Proc Amer Math Soc,1963,14:367-373.

[2] Rowen L H. Polynomial identities in ring theory[M]. New York: Academic Press,1980.

[3] Giambruno A, Sehgal S K. On a polynomial identity forn×nmatrices[J]. J Algebra,1989,126:451-453.

[4] Chang Q. Some Sequence of the stadard polynomial[J]. Proc Amer Soc,1988,104:707-710.

[5] Szigeti J. Permanental polynomial identites on matrix ring[J]. J Algebra,1993,161:90-101.

[6] Domokos M. A generalization of a theorem of Chang[J]. Comm in Algebra,1995,23:4333-4342.

[7] 游松发,郑玉美,胡动刚.欧拉图与矩阵环的多项式恒等式[J].数学进展,2003,32:425-428.