矿柱—顶板力学结构分析

2013-11-14吴昌雄吕力行

中国非金属矿工业导刊 2013年6期

吴昌雄，吕力行

（昆明理工大学，云南昆明 650093）

在采空区中预留矿柱是维持空场法或空场嗣后充填采矿法的顶板安全与采场稳定的最有效办法,它形成对上盘或顶板围岩的支撑。当然,对矿山安全的后果是灾难性的，如果采空区中矿柱的大小、数量、分布形式与顶板的暴露面积之间不能构成比较稳定的力学平衡体系。所以为了确保矿山生产安全，合理确定矿柱的大小数量、机构参数与分布形式显得极其重要[1]。

1 矿柱上方的载荷确定

矿体开采后，在上覆岩层移动过程中，不同性质的岩层所起的作用有所不同，在活动中起承载主体或骨架作用的主要是一些较为坚硬的厚岩层，其他比较柔弱的岩体只起到加载的作用[2]。

不同岩层组成的老顶、直接顶对下方岩层有传递力作用。每个岩层一般承受自身重力和上覆临近岩层相互作用产生的载荷。为了分析方便，假设上覆岩层的载荷是均匀分布的。并假设采场覆岩中有m层岩层，从下至上n(n≤m)层同步变形，各岩层的弹性模量为Ei(i=1，2，3，……，m)，厚度为hi(i=1，2，3，……，m)，体积力为ri(i=1，2，3，……，m)[3]。

由于有n层同步变形，且基于层状岩体中层面上的抗剪切力较弱的考虑，则根据梁理论有公式如下：

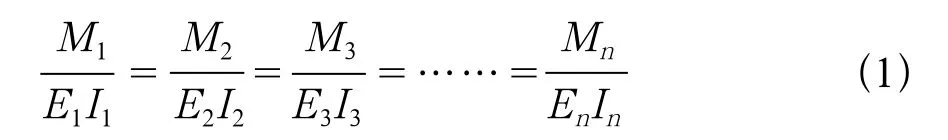
式中：M1、M2、M3……Mn——分别为第1、2、3……n岩层的弯矩；

I1、I2、I3……In——分别为第1、2、3……n岩层的惯性距，I＝bh3/12；

b——梁的横截面宽度。

由(1)式可得：

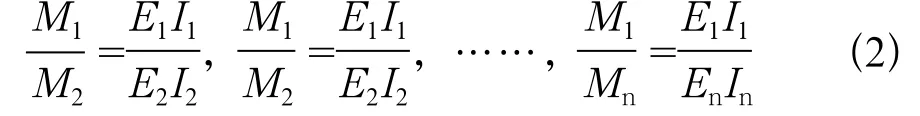
可解得其组合梁的弯矩为：

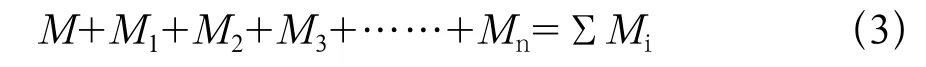
对第1层梁，把式(2)带入(3)有：

根据梁的受力微分原理有：

式中，q为全部(n层)岩层的自重载荷，把q与Ii的表达形式带入上式有：

根据关键层理论可知，覆岩内离层主要发生在关键层下，故只需考虑关键层下位岩层对矿柱的作用[4]。

2 矿柱-顶板力学结构分析

云南某铜矿属古火山岩型沉积变质矿床，Ⅰ3、Ⅰ2矿体规模大，呈层状，似层状产出。

一期开采范围为550m以上的矿体，采用上行式回采。一期投产后，在550～600m水平，采切工程实际揭露两矿体的垂直距离，局部只有1～2m，B30线局部地段两矿体垂直距离为0。矿体倾角5～32°，平均23°，矿体厚度变化大，沿走向矿体顶底板起伏不平，矿岩接触面不清。平均厚度10.66m。中段高度20～25m。

二期开采400～50mⅠ3、Ⅰ2矿体，500～550m标高段平均倾角28°17′24″，平均厚度18.3m。450～500m标高段，平均倾角27°48′36″，平均厚度18.05m，400～500m标高段平均厚度18.21m，平均倾角28°04′12″。大红山铜矿含矿层系一套火山喷沉积变质的变钠质凝灰岩，由石榴黑云白云石大理岩及石榴黑云母角闪片岩等含铜岩石组成。总体上讲，矿岩硬度高。完整性好，属稳固性矿岩。

由于矿岩稳固，f=8～14，该矿多数使用房柱法、空场嗣后充填法开采。一期已开采结束，留下大量不同大小、形状、分布形式的矿柱支撑采空区的顶板。

2.1 矿柱—顶板“简支梁”结构计算[5]

在该矿的开采中，有些采空的顶板可以看作是两侧被矿柱支撑的“梁”结构，因为其开采的范围不大，所以矿柱对顶板的夹持作用不大，则可用“简支梁”考虑岩梁的稳定性[6]。如果在顶板的中间再加入一个矿柱的情况下，顶板受到两端和中间矿柱的支撑作用可用类似于“简支梁”的力学作用模型考虑，受力如图1所示。

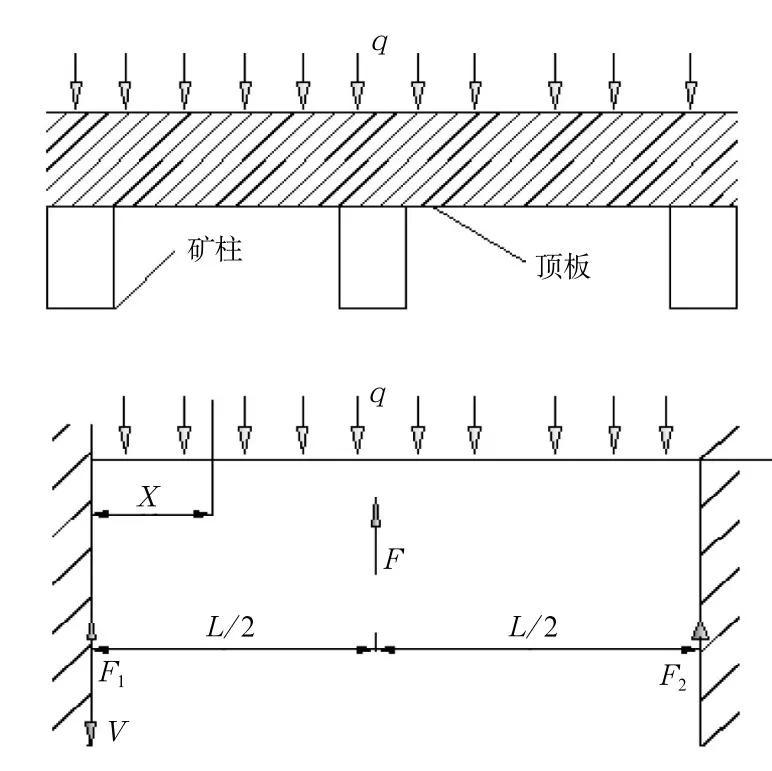
图1 端部和中间大矿柱支撑时矿柱—顶板力学结构

由模型两端的对称性，可以得到：

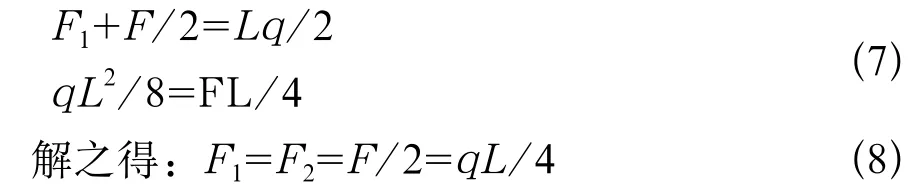
根据材料力学理论，可计算出顶板剪力和弯矩大小如图2所示。从图可知顶板在受到三个巨大矿柱的支撑作用时，在矿柱三个支撑点处受到的剪力为最大(τmax=6q)；在顶板中间，特别是两矿柱的中间受到的弯矩最集中。

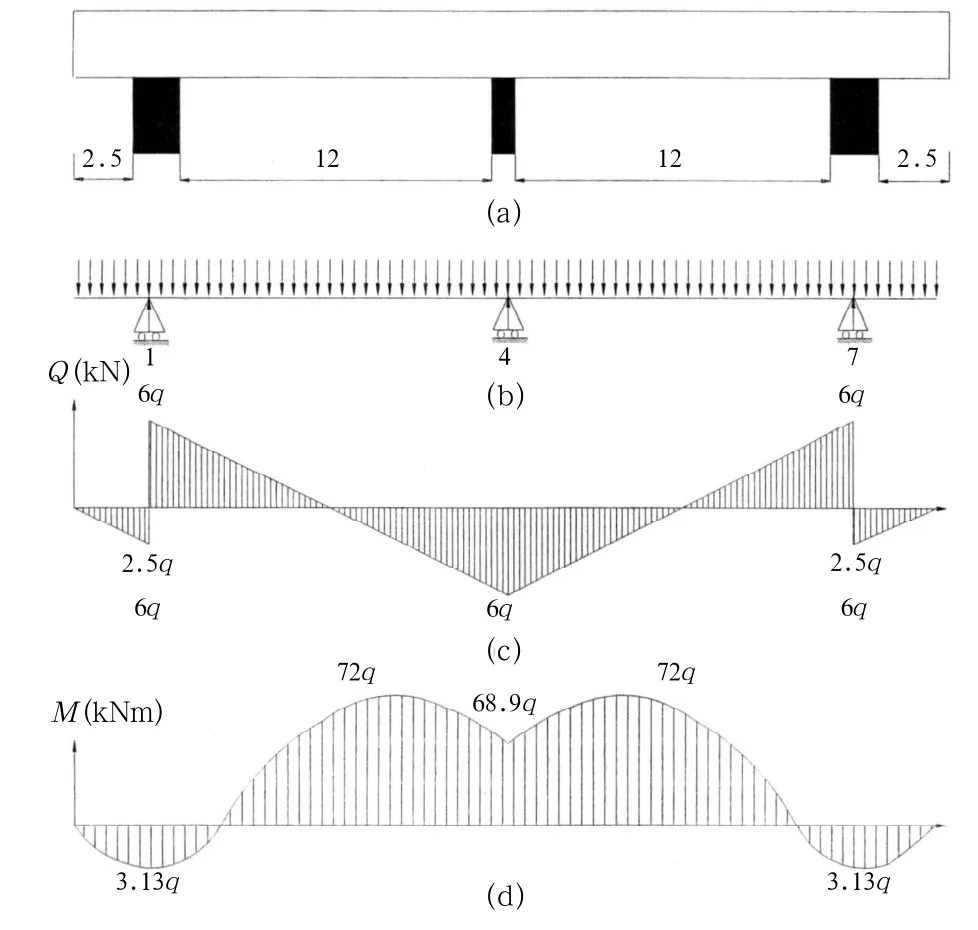
图2 “简支梁”矿柱—顶板应力计算结果

2.2 矿柱—顶板“连续梁”力学结构计算

通过矿柱的强度及载荷理论计算可得[7]，宽1m以上的点柱对顶板有一定的支撑能力，且支撑能力随着矿柱尺寸的增大而增大[8]。

如果一部分大矿柱用一系列点柱替代，计算此时顶板的受力情况。根据以上矿柱和顶板力学作用关系，可简化顶板为上覆条形区域的梁结构，顶板对点柱的力为均布载荷，点柱可看作是一系列可动铰支座对上位岩梁的作用，即视点柱—顶板为“连续梁”模型，模型简化如图3所示。

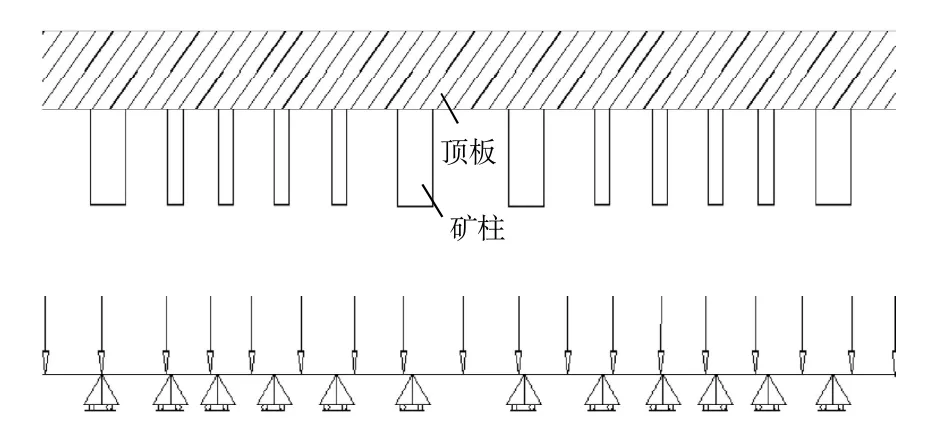
图3 点柱—顶板力学结构模型

根据材料力学理论建立“连续梁”模型，并对其进行求解。在求解过程中，把“连续梁”分解成几个“简支梁”力学结构进行力学分析，建立“三弯矩方程”，最后把各个“简支梁”求解结构组合起来得到“连续梁”的解，具体求解结果如图4所示。

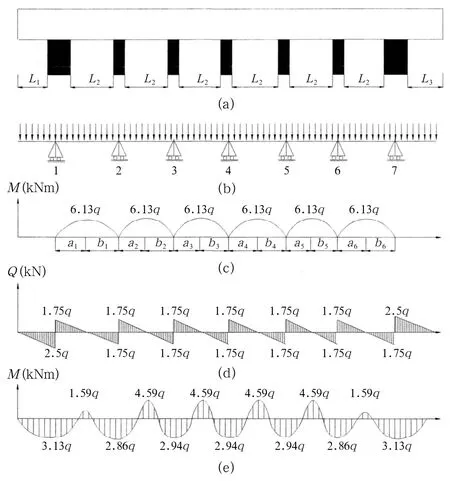
图4 “连续梁”点柱—顶板应力计算结果

图4(b)为点柱—顶板“连续梁”的受力示意图。

下面来对其进行求解：据图4(c)所示，可以计算出各弯矩图的面积分别为：

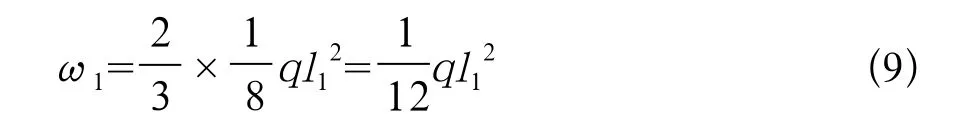
a1=a2=b2=a3=b3=a4=b4=a5=b5=a6=b6

由上可以求得l2/2处为弯矩图面积的形心位置，梁与梁间跨距为l2。在左端，梁有外伸部分，M0=ql1

2/2为支座1上梁截面的弯矩是显然的。现在两两节点对“连续梁”进行力的分析。首先对于1、2节点之间的简支梁跨度写出三弯矩方程，当n=1时，Mn-1=M0=-(1/2)ql12，Mn=M1，Mn+1=M2，ln=l1=l，ln+1=l2=l，an=a1=bn+1=b2，代入三弯矩方程有：

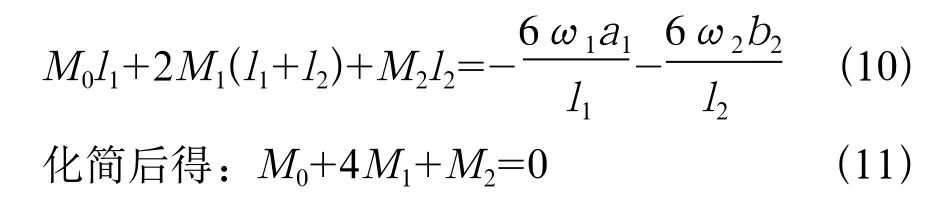
同理对于节点2、3，3、4，4、5，5、6分别可得方程：

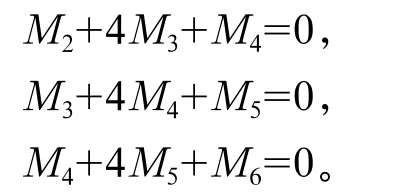
联立方程有：

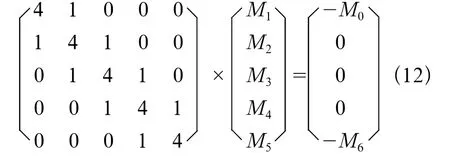
解之有：

对左端第一个简支梁进行分析，列出平衡方程如下：

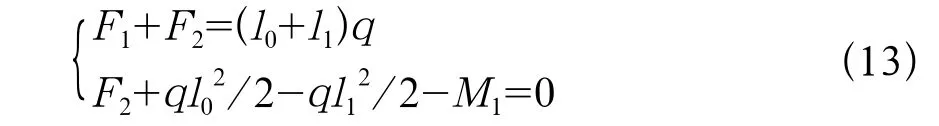
求解有：

同理可以得：

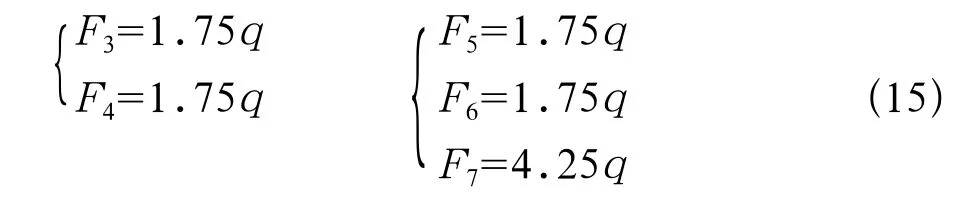
同时可以计算得各弯矩的结果为：

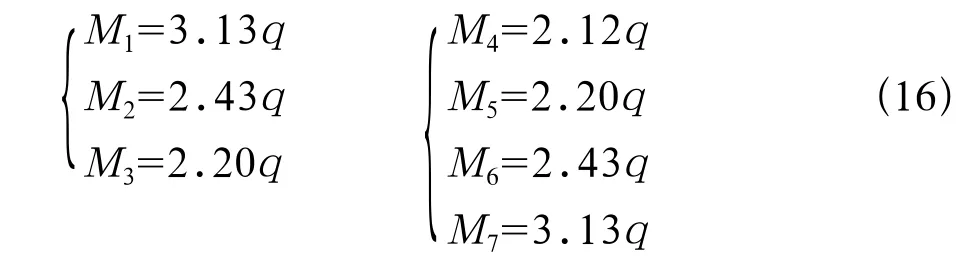
计算得到“连续梁”剪力和弯矩的分布情况如图4中(d)，(e)所示。

从“简支梁”和“连续梁”的计算结果可以看出，在“简支梁”模型中顶板在三个交点处所受的剪力最集中(大小为6q)，顶板所受的弯矩在整个中间区域，特别是两矿柱中间比较集中，其最大弯矩为72q，并且它们的数值较大；而“连续梁”所受的剪力和弯矩作用比较平均，其最大剪力为2.5q，最大弯矩为4.59q，且它们的数值较小。由此可以看出，由三个大矿柱支撑的顶板稳定性远远没有一系列点柱支撑的顶板稳定性好。