基于PCA 的相似度方法在半导体产品分类中的应用

李秀玉，张 成，逄玉俊

(沈阳化工大学 信息工程学院，辽宁 沈阳 110142)

在半导体工业中，过程变量包含了工业过程的运转信息以及产品的生产状况，由于产品的生产工况不同，导致在生产过程中各变量呈现出不同的相互关系.在间歇过程中，通过比较不同批次的原料数据、过程变量数据等信息对产品进行分类，以寻求工业过程的最佳工作条件，对提高产品质量和效率具有重要的意义.

主元分析方法PCA 在工业过程中已经得到了广泛的应用.直接对工业采集到的数据进行操作，计算量非常大，降低了故障检测系统的实时性.为了解决这一问题，利用PCA 方法提取原始数据中的主要信息，将高维数据降为低维数据的同时，保存了原有数据的主要信息，从而提高故障检测系统的实时性［1］.

利用PCA 数据驱动方法对分析间歇过程多批次数据的相似度及数据分类具有重要的意义.1998 年Jaeckle 和MacGregor［2］利用主元回归思想提出了基于相同特征参数的窗口，利用窗口对原始数据分类;Lane，Martin，Kooijmans，et al［3］利用PCA 提出了一种能够实时监测产品等级的思想;Krzanowski［4］利用PCA 对原始数据进行建模，并衡量每个PCA 模型负载矩阵之间角度的大小;Johannesmeyer et al［5］利用相应的特征值加权负载矩阵衡量不同批次的相似度;2008 年Gunther，Baclaski，et al［6］将PCA 相似因子应用到生物间歇过程中，利用交叉验证的方法确定建立PCA 模型时所需主元的个数，通过比较不同批次数据的相似度，对不同工况下采集到的数据进行分析.本文将相似因子方法应用到半导体间歇过程数据中，在保留原始数据主要方差信息情况下，对多批次数据进行相似度分析，以达到对半导体工业过程不同工况数据相似度分类的目的.

1 基于PCA 的相似因子

1.1 PCA 理论

PCA 方法是一种将变量相关的原始数据转化为线性无关的主元变量数据的方法，揭示了数据变量的主要方差信息.降维后主元个数A≤J，J 代表过程变量，第一主元包含原始数据的最大方差信息.

首先对半导体间歇过程数据XI×K×J(I 代表数据批次，K 代表时间，J 代表过程变量)进行标准化处理，由于产生不同批次数据的工业过程工况不同，为了保留各批次数据之间的差异性［7］，采用批次间的标准化方法，如(1)式所示.

其中¯xkj为第k 批次第j 个变量的均值，skj为第k批次第j 个变量的标准差.

式(2)为标准化后的第i 批数据.

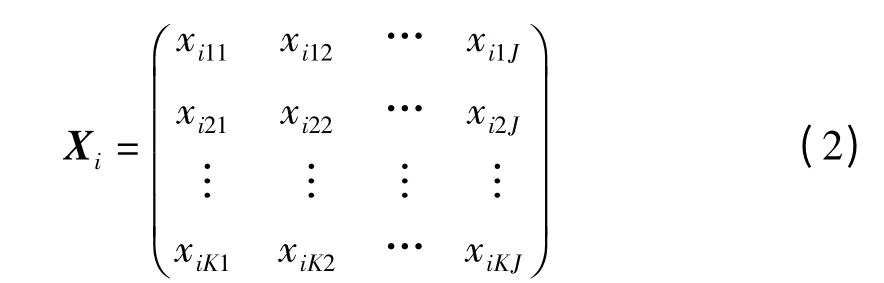
PCA 方法的具体公式:

其中Pi是i 批数据标准化后协方差矩阵的特征矩阵，Ti∈RK×A为i 批数据标准化后协方差矩阵的得分矩阵，Ei为第i 批数据的残差矩阵.

1.2 PCA 相似因子

由于不同工况的间歇过程数据变量之间的相互关系不同，导致不同批次数据负载向量之间出现角度偏离.利用PCA 相似因子［6］来衡量两个主元模型相应负载向量之间的角度大小，PCA相似因子定义为:

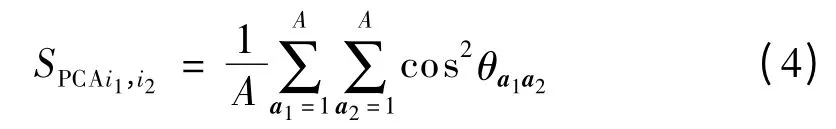
其中θa1a2表示第i1批数据负载矩阵的第a1个负载向量与第i2批数据负载矩阵的第a2个负载向量之间的角度.

公式(4)可以写成:

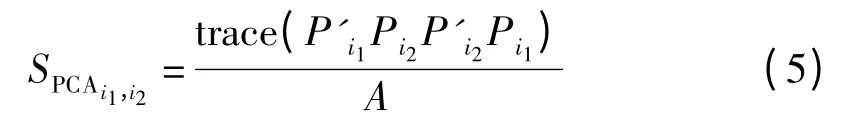
由式(5)可得:当i1=i2时，SPCA=1，当两个批次的负载矩阵正交时为0，所以取值范围为［0 1］.

1.3 改进的PCA 相似因子

在半导体间歇过程原始数据的PCA 模型中，不同主元包含原始数据的方差信息各不相同，为了体现各主元包含不同的方差信息量，SPCA只是利用负载向量之间的夹角大小作为批次数据的相似度指标，并没有考虑方差信息的差异，所以，在进行实验仿真时不能得到理想的分类效果，如图3、4 所示.对PCA 模型的负载向量利用相应的特征值进行加权，利用加权的PCA 相似因子来衡量相似度大小.特征值存在的关系为:

λ1＞λ2＞…＞λA，其中λ 为协方差矩阵的特征值.

加权的PCA 相似因子［6］为:

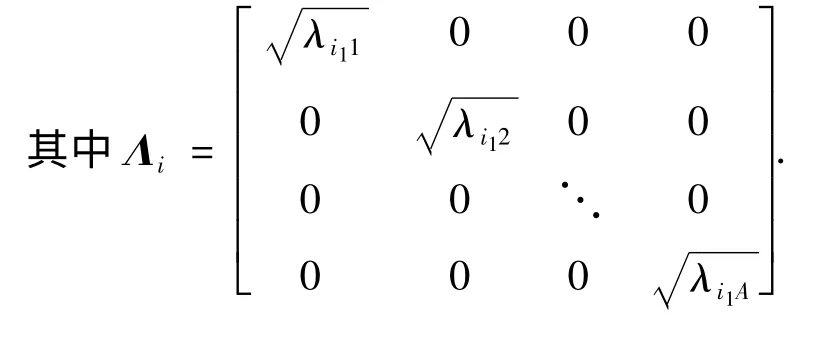
2 半导体数据仿真结果与分析

文中利用半导体工业实例进行不同批次数据的相似度比较.在半导体工业过程中采集到来自3 类不同实验操作的107 批次数据［8］(1～34批次为第一类实验数据，35～70 批次为第二类实验数据，71～107 批次为第三类实验数据)，三类实验是在三种不同工况下进行的.选取其中两个变量Endpt A 与TCP Load 分析数据的轨迹，如图1 所示.在图1 中，变量Endpt A 的数据轨迹呈现三种不同分布，可知107 批次的数据来自三种不同工况的实验过程.

对于主元个数的选取，主要的方法有［9］:累计方差贡献率、可预测残差平方和、数据信噪比等.文献［6］利用交叉验证的方法获得建模的主元个数.本文为了保留原始数据的大量信息，采用累积贡献率法确定主元个数，分别以第一类实验的第21 批，第二类实验的第56 批，第三类实验的第78 批为例说明主元个数的确定方法.

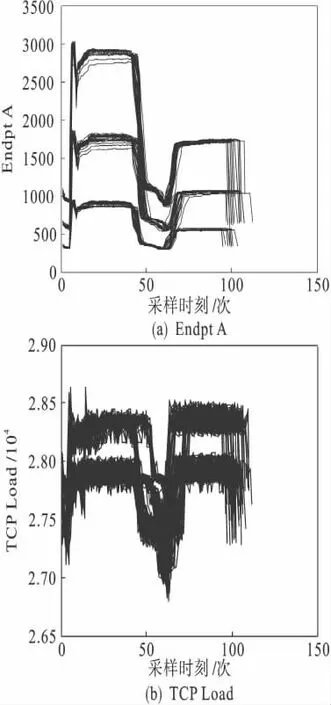
图1 变量Endpt A 与TCP Load 的轨迹图Fig.1 The trajectory of Endpt A and TCP Load

图2 分别为第21、56、78 批数据的各个主元累计方差贡献率，为保留原始数据70 %以上信息以及比较SPCA与的差别，主元个数分别取7 和10.

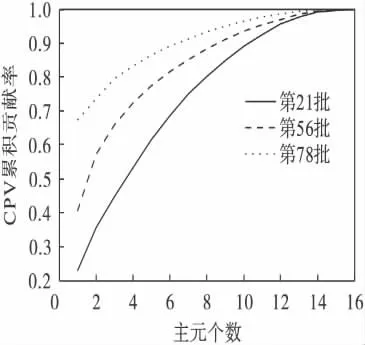
图2 主元累计方差贡献率Fig.2 The cumulative percent variance of principle components

为了说明方法的有效性，实验分别取三类实验的3 个批次作为参考批次，即第21、56、78 批次，得出其余批次与参考批次的相似度.

取主元个数为7，进行实验仿真，得出结果如图3 所示.

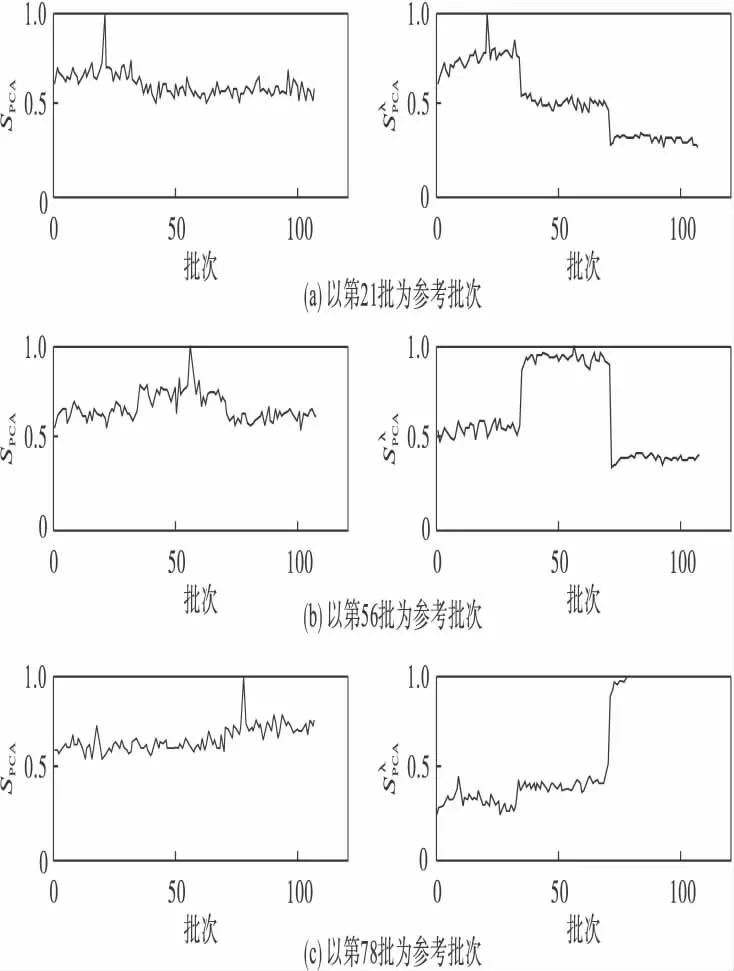
图3 主元个数A=7 时相似度比较结果Fig.3 Similarity results when principle components’number A=7

在图3 中，图a、b、c 分别为以第21、56、78批为参考批次结果.利用方法可以将原始数据的相似度分成三个不同区域，图a 中，与第21批次数据在同一工况下采集到的数据(第1-34批)相似度接近1 且最大，在其它两个工况下采集到的数据(第35-107 批)所计算出的SλPCA指标相比较小，呈现出两个不同的范围;在图b、c 中分别以第二、三类工况下采集的数据为参考批次，可以得到与图a 相吻合的分类效果.这与通过分析式(6)及前面变量曲线轨迹相一致，具有理想的分类效果.

保留原始数据85 %以上的方差信息量时取主元个数A=10，得到实验仿真结果如图4所示.

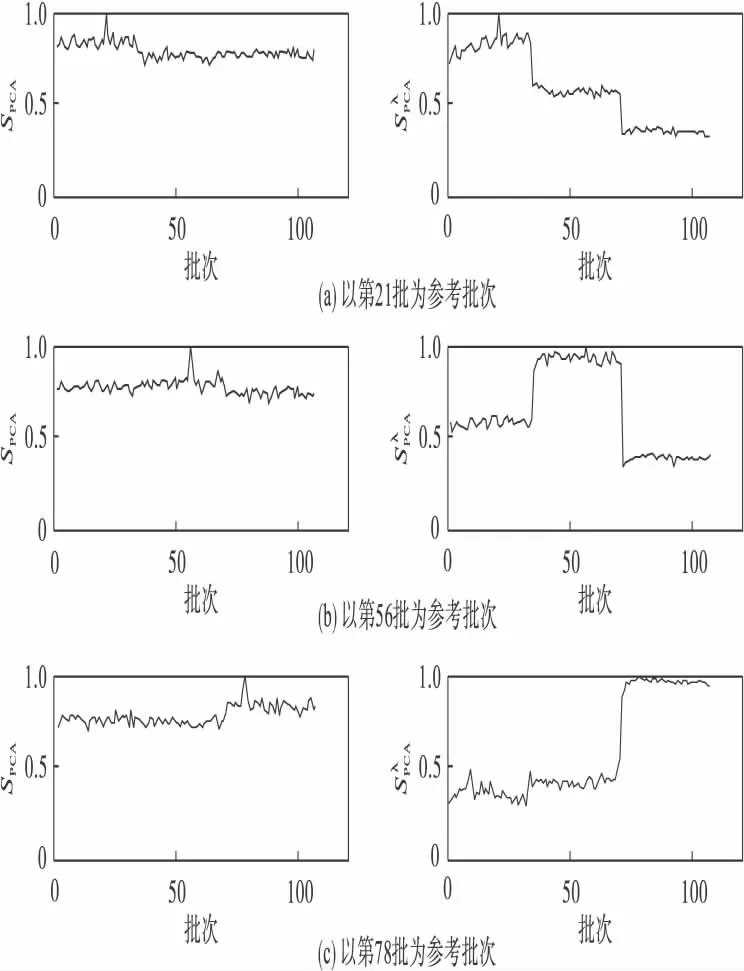
图4 主元个数A=10 时相似度比较结果Fig.4 Similarity results when principal components’number A=10

在图4 中，图a、b、c 分别为以第21、56、78 批为参考批次结果.分类结果与当主元个数为7 时基本一致，利用均能得到理想的分类效果.

通过仿真结果，采用批次间的标准化方法，在保留原数据主要信息的条件下，利用能够实现对半导体工业间歇过程不同工况下多批次数据的分类.

3 结论

以半导体工业过程为对象，基于传统的PCA 方法建立模型，利用协方差矩阵特征向量之间的角度衡量原始数据各批次的相似度，并将其运用到半导体间歇工业过程数据中，对来自三类不同实验的多批次数据进行相似度比较，实验结果表明:利用方法对半导体间歇过程不同工况数据的分类具有理想效果，对间歇过程数据的分类和故障检测具有重要意义.

［1］He Q Peter，Wang Jin.Statistics Pattern Analysis:A New Process Monitoring Framework and its Application to Semiconductor Batch Processes［J］.AIChE Journal，2011，57(1):107－121.

［2］Jaeckle C M，MacGregor J F.Product Design Through Multivariate Statistical Analysis of Pdata［J］.AIChE Journal，1998，44(5):1105－1118.

［3］Lane S，Martin E B，Kooijmans R，et al.Performance Monitoring of Amulti-product Semi-batch Process［J］.Journal of Process Control，2001，11(1):1－11.

［4］Krzanowski W J.Between-groups Comparisons of Principal Components［J］.Journal of the American Statistical Association，1979，74(367):703－707.

［5］Johannesmeyer M C，Singhal A，Seborg D E.Pattern Matching in Historical Data［J］.AIChE Journal，2002，48(9):2022－2038.

［6］Gunther J C，Baclaski J，Seborg D E，et al.Pattern matching in Batch Bioprocesses—Comparisons Across Multiple Products and Operating Conditions［J］.Computers and Chemical Engineering，2009，33(1):88－96.

［7］Wold S，Kettaneh N，Fridén H，et al.Modelling and Diagnostics of Batch Processes and Analogous Kinetic Experiments［J］.Chemometrics and Intelligent Laboratory Systems，1998，44(1/2):331－340.

［8］Wise Barry M，Gallagher Neal B.A Comparison of Principle Component Analysis，Multiway Principle Component Analysis，Trilinear Decomposition and Parallel Factor Analysis for Fault Detection in a Semiconductor Etch Process［J］.Journal of Chemometrics，1999，13(3/4):379－396.

［9］周东华，李钢，李元.数据过程驱动的工业过程故障诊断技术［M］.北京:科学出版社，2011:59－64.