基于马氏链模型和模拟退火算法的最优证券投资组合

李旭坤

（华中师范大学数学与统计学学院，湖北 武汉 430079）

一、引言

证券投资是在证券市场上购买有价证券，以利息、股息或出售赢利等形式取得利润收益的一项经济活动。证券投资者最关心的是投资收益率的高低及投资风险的大小，投资者在选择投资策略时，总希望收益率大而风险小，但二者不可能同时满足。在给定的收益率下，确定投资策略使投资风险最小，是投资者最关心的问题。

现代证券组合理论是关于在收益不确定条件下投资行为的理论，它由Markowitz提出，认为理性的投资者应该具有“非满足性”和“风险回避性”两个特征。

一般认为，证券市场是弱有效的，历史信息已反应在当前价格中，证券未来的价格仅与当前状态有关，而与过去无关。大量的研究也证明了证券价格具有马氏性，因此利用马氏链模型进行研究是合理的。Markowitz模型要求协方差矩阵是正定的，但是这条件在现实中并不具有一般性。模拟退火算法为我们提供了一种数值计算的解决方法。

二、马氏链模型

定理 对时齐马氏链，如果存在正整数d，对任意的i,j∈S，都有pij(d)≥0，则此链具有遍历性，且有极限分布π＝（π1,π2,…，πn)。

将证券价格的状态空间划分为{上涨，稳定，下跌}，用{1,2,3}表示，即状态空间S={1,2,3}。转移概率用一个状态转移到另一状态的频率代替，即因此，转移矩阵为：

建立马氏链模型，首先要判断证券价格是否具有马氏性。设pi服从自由度为(n-1)2的x2分布，利用Y统计量对证券价格的马氏性进行假设检验。前人研究证明[1]，原假设被拒绝，即认为证券价格具有马氏性。本文在设计ma t l a b程序时也对证券价格进行了x2检验。

三、模拟退火算法

Markowitz的均值—方差模型如（1）描述，其中X=(X1,X2,…,Xn)是投资组合，Σ是协方差矩阵，R=(R1,R2,…,Rn)T是证券的收益率向量，R P是投资者的期望收益。均值—方差模型的经济学意义在于使用方差衡量投资风险，投资者可预先确定一个期望收益，通过该模型确定在每种证券上的投资比例，使证券组合的投资风险最小。不同的期望收益会存在不同的投资组合，使得方差最小。

由于算法最终解有可能并不是最优解，本文参考前人的研究成果[2]，在设计matlab程序时增加了一个停时器，其作用是将退火过程中的最优解记录下来，并最终输出最优解。本文取初始温度T0=200，最终温度 e=0.0001，降温系数是 at=0.99,Tk+1=at*Tk，每一温度下的迭代次数L=500。在初始状态的选取上，使用Monte Carlo方法求得一个较好的初始解。

模型（1）中证券不允许卖空，这与中国的市场现状是符合的。由于要求证券组合的和为1，所以要对新解进行归一化处理，保证其和为1。相邻状态的产生规则是产生一个0和1间的随机数，新解X'=X+scale*[rand(1)-0.5]，scale是自领域适应因子[3]，初值scale0=1，下降系数与降温系数一样，scalek+1=at*s c a l ek，与温度下降类似，它在迭代开始时较大，在结束时较小。优化函数为J(X)=XΣXT-(XR-RP)2，最优证券投资组合就是使得目标函数J(X)最小且满足相应约束条件的X。

当出现新解的某个分量小于0或大于1时，本文采用的方法是用旧解中相应位置的分量去代替。

四、实证分析

本文选取平安银行2011年12月30日至2013年3月25日共304个交易日收盘价数据进行实证分析，实际有效数据为290天[4]。通过ma t l a b计算，发现平安银行的价格具有马氏性，这与已有的研究成果相一致，因此可以使用马氏链模型去进行研究。计算可得转移矩阵，如（2）所示：

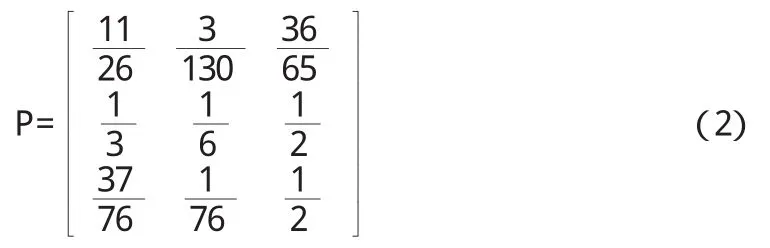
转移矩阵表明无论平安银行当前股价处于什么状态，未来上涨或下降的概率都接近0.5，股价维持不变的可能性非常低，符合市场实际情况。由定理知，转移矩阵同时表明该马氏链是遍历的，且存在极限分布limP，如（3）所示。

极限分布表明平安银行下跌的概率约为45%，上涨概率约为52%，股价维持不变的可能性非常小，因此，对平安银行股价未来的趋势判断是上涨。同样地，可以对其他证券进行类似操作。接下来，选取十只上涨概率较大，即未来表现较好的证券作为投资组合的证券，通过马氏链模型的筛选，分别为保利地产、格力电器、贵州茅台、农业银行、上汽集团、万科A、招商银行、中国建筑、中国平安、中信证券，选取2012年11月14日到2013年3月29日共90个有效交易日的收益率数据进行模拟退火算法的实证研究[4]。

证券的收益率Ri用历史收益率数据序列{ri}的期望值去代替，因为收益率围绕均值上下波动，用期望值去近似代替收益率是合理的，即Ri=E(ri)。取期望收益率R P等于日无风险利率0.000086，因为如果证券投资组合的收益率小于无风险利率，投资者可以直接投资短期国债而无需承担风险。表一是用Monte Carlo方法得到的初始解，表二是用模拟退火算法求得的最优解，其风险比初始风险要低，同时收益率也比初始值要低，这符合经济学原理，风险和收益是正相关的。最优解的优化函数值小于初始解的优化函数值，这表明在相同的收益率下，最优解要比初始解的证券投资组合风险要小。

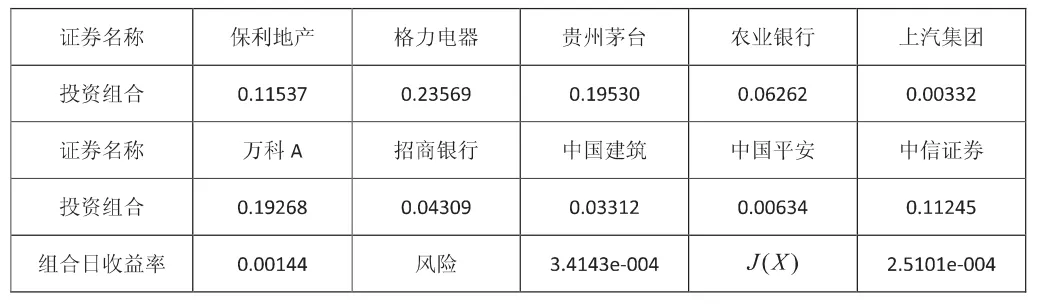
表一 Monte Carlo方法

表二 模拟退火算法

五、结论

在证券市场具有马氏性这一条件下，利用马氏链模型选取十只未来预期表现较好的证券，再利用模拟退火算法，避开了均值—方差模型当中协方差是正定的要求，得到最优证券投资组合，结果令人满意。

[1]王新蕾，肖东荣等.股指马氏性的检验和预测[J].统计与决策，195：21-22，2005.

[2]庞峰.模拟退火算法原理及算法在优化问题上的应用[D].硕士学位论文，吉林大学，6-7，2006.

[3]肖思和，鲁红英等.模拟退火算法在求解投资组合优化问题中的应用研究[J].四川理工学院学报（自然科学版），23(1)：116-118，2010.

[4]北京聚源锐思数据科技有限公司.锐思金融数据库.http：//w ww.resset.cn.