Bland-Altman法对大学生20-MST有氧耐力评价的有效性研究

张敏青

(浙江理工大学 体育教研部，浙江 杭州310018)

·运动人体科学·

Bland-Altman法对大学生20-MST有氧耐力评价的有效性研究

张敏青

(浙江理工大学 体育教研部，浙江 杭州310018)

Bland-Altman分析是评价测验成绩有效性的优选方法之一。研究采用Bland-Altman技术对大学生20m多级往返跑(20-MST)中有氧耐力评价的有效性进行了实验研究，实验研究结果显示：单纯用相关系数对20-MST中有氧耐力进行评价不够全面，在消除系统偏倚后，乃是有效的评价方法。用1st20-MST测验成绩建立预测2nd测验成绩的线性回归方程为：Y=1.995+0.879X(Y：2nd测验值；X：1st测验值)。R=0.746，plt;0.01。

20-MST；Bland-Altman分析；有效性；评价

0 前 言

20m多级往返跑测验(multistage 20 meter shuttle run test，简称20-MST)是一种间接测定人体有氧耐力的机能测验。目前国内外对20-MST评价人体有氧耐力的有效性的研究较少，对它的研究主要采用简单的相关分析方法。近来，很多研究者指出相关分析在评价有效性(一致性)问题上存在缺陷，对系统误差不敏感，目前国内对20-MST的有效性研究尚未见报道。本文采用Bland-Altman方法分析了我国女大学生20-MST测验的有效性，提出了消除系统偏倚的一些统计技术。

1 实验对象与研究方法

1.1实验对象

无心肺疾病或运动系统疾病的健康女性大学生56名(年龄19.1±0.5，身高160.4±4.1cm，体重52.6±6.5kg)。实验前24h内未从事剧烈运动。受试者在室外塑胶田径场上每间隔一周，在相同时间、相同场地上进行20-MST测验，前后共进行了3次测验。

1.2研究方法

1.2.1 20-MST测定。 测验前用录音带上的校正信号对录音机的走带速度进行校正,使走带速度的误差被控制在1stmin-1 范围内。受试者在两端划有端线,长度20m的跑道上,以踏上或踏过端线为标准进行往返跑。用录音带上预先设定好时间间隔的节奏控制受试者的跑速,单声“嘟”控制完成每一段20m跑的速度,连续3声的“嘟”提示受试者应加速达到更高一级跑速。20-MST 的起始速度为 8.5km·h-1 ,每分钟递增0.5km·h-1 (即每分钟跑一个级别)。测验过程中，要求受试者尽最大努力完成本人所能达到的最高跑速级别，当受试者经反复鼓励,仍连续2次不能在规定时间内按要求踏上或踏过端线,或的确感到无法坚持运动时,终止测验,记录员记录受试者最后阶段的完成等级。

按最大有氧速度(Maximal aerobic speed,MAS，km·h-1) =8+0.5Lmax(Lmax为完成等级)计算最大有氧速度。按王翔等学者建立的预测中国大学生VO2max的回归方程：最大吸氧量(maximal oxygen uptake,VO2max，ml·kg-1·min-1)：VO2max=-21.960+5.739 ×MAS。计算VO2max。

例如：受试者王红在20-MST测试中，完成7.8等级，那么她完成的最大有氧速度、最大吸氧量分别为，MAS=8+0.5×7.8=11.9( km·h-1)，VO2max=-21.960+5.739 ×11.9=46.3 (ml·kg-1·min-1)

1.2.2 统计学处理。 使用SPSS11.5 for Windows统计软件进行，包括单因素方差分析、相关分析、回归模型建立、回归模型假设检验、回归模型适合性检验等。显著性水平取双侧0.05。使用MedCalc statistical software 9.5进行Bland-Altman分析统计，对第一次(1st)与第二次(2nd)、第二次(2nd)与第三次(3rd)，第一次(1st)与第三次(3rd)测验数据进行95%一致性限(Limits of Agreement，LoA)的分析。

2 研究基本结果与分析

2.1受试者三次20-MST测验结果

受试者三次20-MST测验结果如表2所示。相关分析显示，1st的测验结果与2nd， 3rd的测验结果均存在显著性相关(P lt;0.01)，2nd测验结果与3rd测验结果也存在显著性相关(P lt;0.01)。

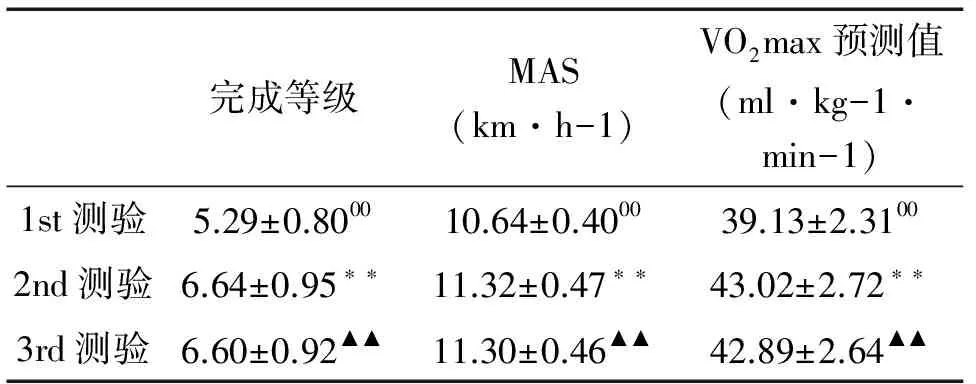
表1 受试者三次20-MST测验结果(M±SD)

注：*代表1st测验与2nd测验结果相关分析的结果，**P lt;0.01；0代表1st测验与3rd测验结果相关分析的结果，00P lt;0.01；▲代表2nd测验与3rd测验结果相关分析的结果，▲▲P lt;0.01

2.2三次测验结果的单因素方差分析

对1st、2nd、3rd测验结果进行单因素方差分析显示，1st与2nd、3rd之间， 20-MST完成等级、MAS和VO2max预测值，均存在显著差异(Plt;0.01)。2nd与3rd之间不存在统计学意义的差异。

表2 三次测验结果的单因素方差分析

注：**P lt;0.01；表4，6同

2.3 Bland-Altman图谱分析

56受试对象配对数据的差值的均值为1.36，图2，差值的标准差±0.64，则95%一致性限为1.36±1.96×0.64，即(0.1-2.61)；同理，图2的一致性限为0.06-2.56；图3的一致性限-0.58-0.49。有研究者指出，两组数据的一致性程度越高，代表差值均数的实线越接近代表差值均数为0的假想虚线。同时最大差值/测验平均值的比值小于1/6，即认为两次测验一致性程度较高。从图1、图2、图3中可以看出，2nd与3rd测验的差值的均值接近差值均数为0的假想虚线，同时其最大差值为0.7，与两次测验结果平均值的比值小于1/6。而1st与2nd、3rd测验之间的图谱分析显示，两者与差值均数为0的刻度线存在一定距离，在实验中也发现，1st与2nd测验，与3rd测验的最大差值均为3.4，与两次测验结果平均值的比值均大于1/6。

2.4两种统计方法间的一致性比较

有效性评价即一致性评价。采用不同的方法对三次测验结果进行一致性评价，简单相关分析得出1st 与2nd、1st 与3rd、2nd 与 3rd之间均存在非常显著性相关，相关系数分别为0.75、0.74、0.96。表4中Bland-Altman分析得出的一致性限，并结合图1、图2、图3，得出2nd 与 3rd测验结果具有良好的一致性，而1st 与 2nd、1st 与3rd之间存在较大的系统偏倚(bias)。

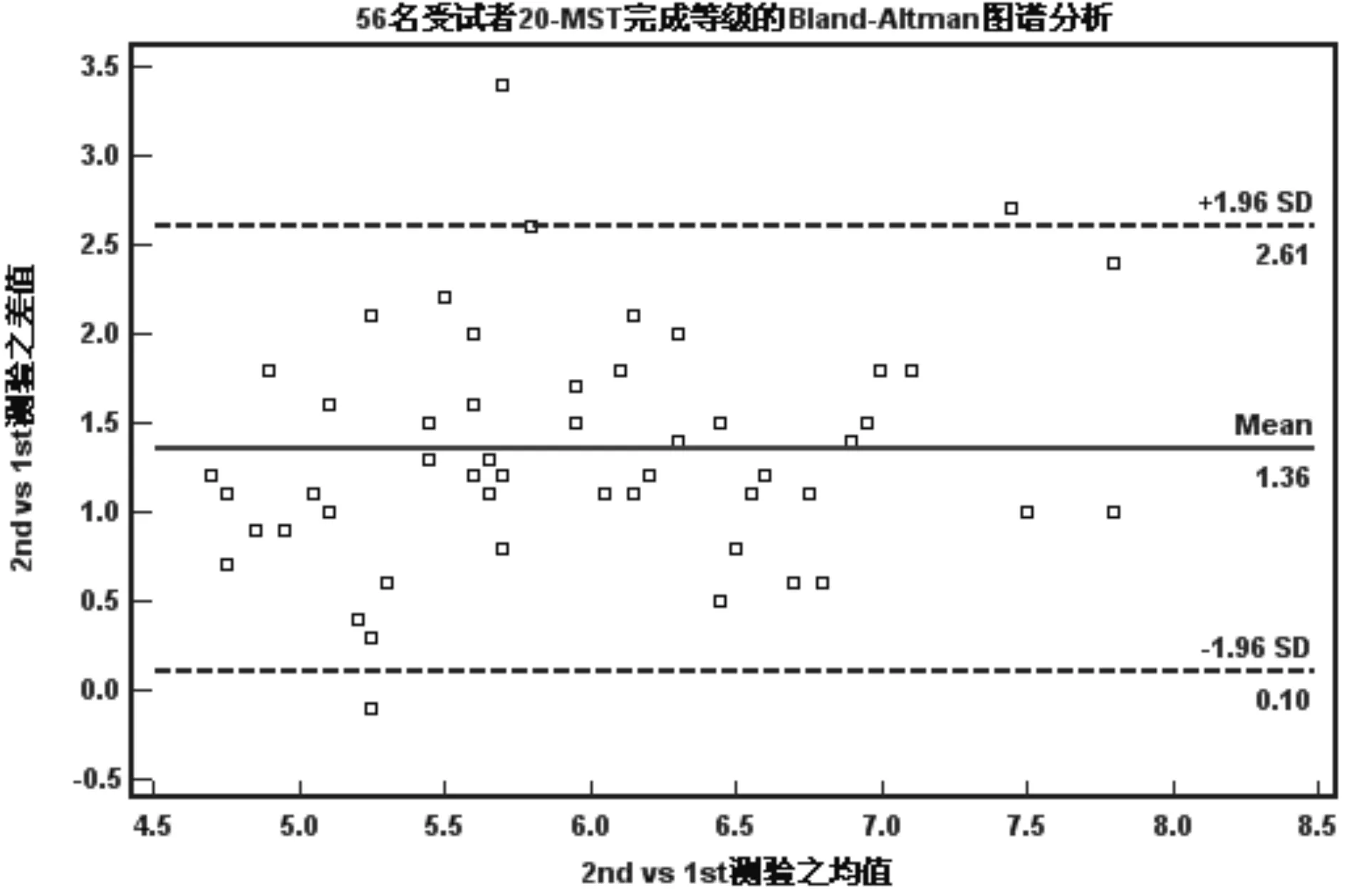
图1

图2

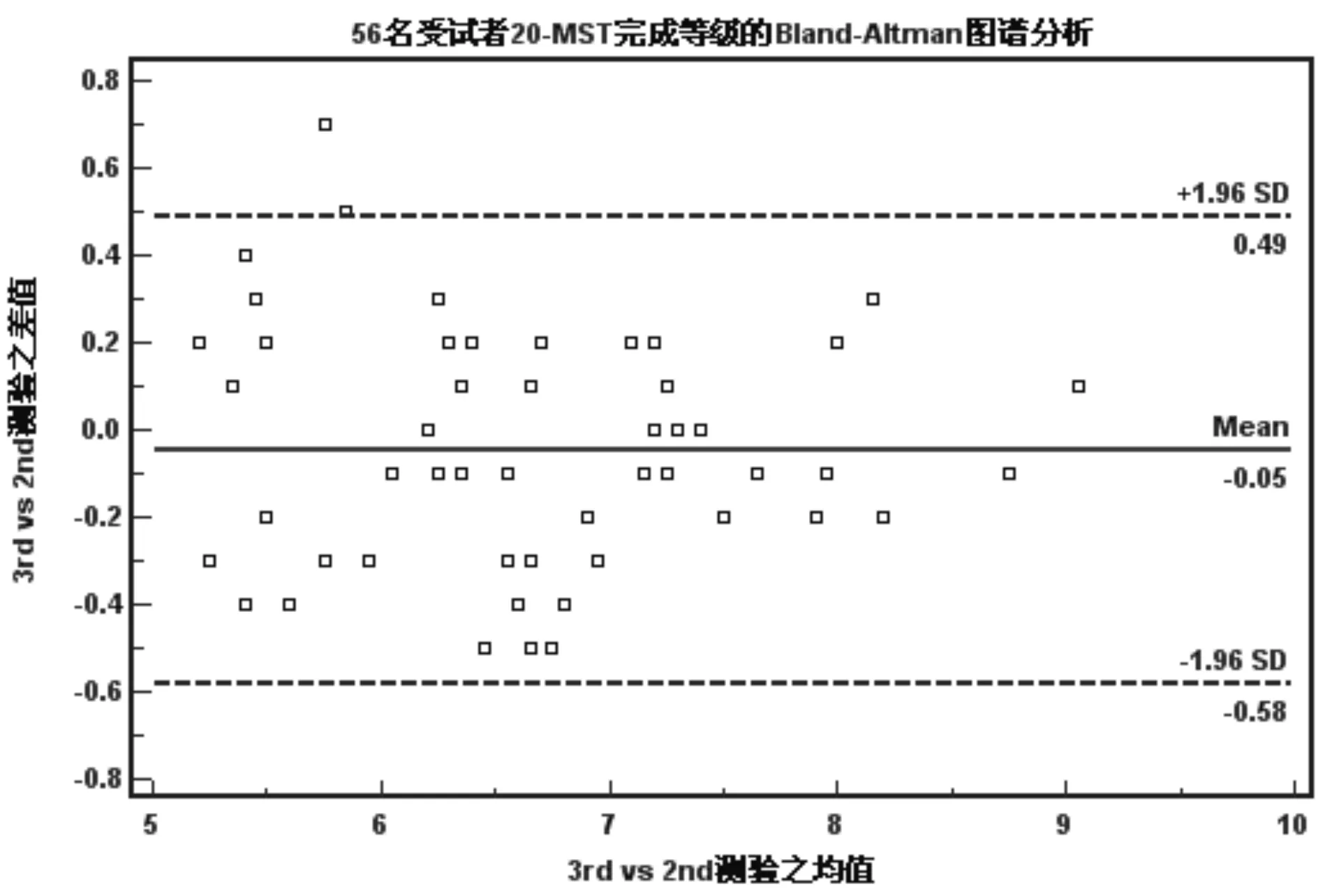
图3

表4 两种统计方法间的一致性比较结果

2.5三次测验结果的单因素方差分析

由表5、表6可知，1st 与 2nd、1st 与3rd的测验结果存在很大的偏倚，分别为1.36±0.64、1.31±.64。其变异度为26.53±0.14%、25.7±0.14%。单因素方差分析的结果也显示31与32、21与32存在显著性差异，而31与21则无显著性差异。支持了Bland-Altman点图样分析结果。

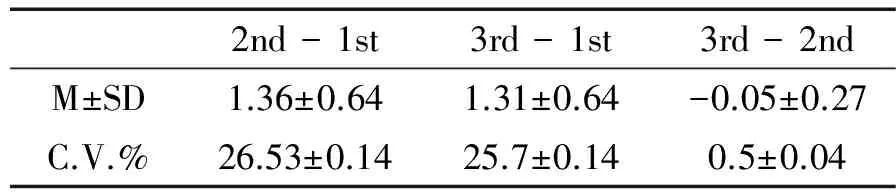
表5 三次测验结果的差值进行单因素方差分析

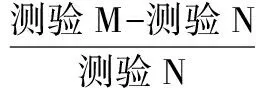
表6 差值进行单因素方差分析结果一览表

注：21表示2nd测验数据与1st测验数据的差值，31表示3rd测验数据与1st测验数据的差值，32表示3rd测验数据与2nd测验数据的差值，21 -31表示两组差值间的比较

2.6 1st20-MST与2nd20-MST之间的回归方程式

以1st 20-MST测验数据为自变量，2nd 20-MST测验数据为因变量，建立的线性回归模型为Y=1.995+0.879X(Y：2nd测验值；X：1st测验值)。R=0.746，plt;0.01。

线性回归模型的统计学检验。

①线性关系检验。 方差分析的结果为F=67.743，P=0.000，表明1st测验和2nd测验结果之间有明显的线性关系。回归分析结果显示，常数项和1st测验值对应的系数，其t检验的sig.值分别为0.001和0.000，具有显著的统计学意义。

②回归模型拟和度检验。 回归直线拟和优度检验的指标是判定系数R2。R2越接近1,说明拟和优度越好。本研究中回归模型的判定系数(R2)和判定系数修正值(R02)分别为：R2=0.556 ，R02=0.548 ，表明回归模型具有较好的拟合度。

③残差独立性检验和正态性检验残差的独立性检验。 主要通过Durbin-Watson 检验来完成。Durbin-Watson 检验的参数用D 表示。D的取值为0-2，若D=2，说明回归模型中的随机误差项独立，若D接近0，则随机误差项不独立。如果随机误差项不独立，那么对回归模型的任何估计与假设所做出的结论都是不有效的。本研究中Durbin-Watson检验的结果为D=1.635，比较接近2，表明模型中的随机误差项具有独立性。通过观察回归模型的标准化残差直方图(图4)和标准化残差正态P-P图(图5)发现，由于残差具有正态分布的趋势。因此认为本研究建立的模型是恰当的。因此，可以用受试者第一次20-MST测验的数据代入Y=1.995+0.879X,获得一个排除学习或练习因素影响的、较为符合实际的完成等级值。

图4

图5

3 结论与建议

3.1 本研究结果分析表明，20-MST的1st测验数据与2nd、3rd测验数据间均存在显著性相关，显示三组数据具有良好的线性相关关系，而Bland一Altman分析显示，1st与2nd、3rd测验数据间存在很大差异，LoA分别为1.36±.64、1.31±.64，变异系数达26.53±.14%，25.7±.14%，而2nd与3rd测验中，LoA为-0.05±.27，一致性限范围狭窄，因此本研究认为2nd与3rd测验具有良好的一致性。

3.2 通过对各组的测验结果进行单因素方差分析结果显示，1st与2nd、3rd测验结果间均存在显著性差异，2nd与3rd测验结果间无统计学差异。本研究结果进一步验证了K.L.Lamb研究中，1st与2nd测验值间存在较大的系统偏倚，20-MST具有学习效应的观点。20-MST测验具有学习或练习效应，2nd的测验值明显高于1st的测验值，而2nd与3rd的测验值间无显著性差异。因此1st 20-MST的测验结果不能真实的反映人体的有氧耐力水平，2nd的测验结果是可信的。

3.3 通过本研究，可以认为单纯用相关系数去评价20-MST的有效性是不全面的，相关系数反映的是两变量线性关系的密切程度而非一致性，且对系统误差不敏感。而Bland一Altman是定量分析与定性分析的有机结合，同时兼顾系统误差和随机误差，是评价一致性问题时优先选择的方法。

3.4 本研究中建立了用1st的20-MST测验成绩预测2nd测验成绩的线性回归模型。方差分析、Durbin-Watson检验、标准化残差直方图、P-P图分析等表明该模型满足线性回归模型独立、线性、正态和等方差四个假设条件，具有良好的适合性。用1st 20-MST的测验成绩建立的预测2nd测验成绩的线性回归模型为：Y=1.995+0.879X(Y：2nd测验值；X：1st测验值)。R=0.746，plt;0.01。

[1] 陈卉.Bland一Aitman分析在临床测验方法一致性评价中的应用[J].中国卫生统计，2007，24(3):308-310.

[2] 李锐冲,李晓松.两种测验方法定量测验结果的一致性评价[J].现代预防医学，2007，34(17):3263-3269.

[3] Kevin L.Lamb Louise Rogers. A re-appraisal of reliability of the 20 m multi-stage shuttle run test [J].Eur J Appl Physiol，2007，100:287-292.

[4] Fairbrother A,Jones MA,Hitchen PJ.Reliability and concurrent validity of the multistage shuttle test in adolescent athletes[J]. J Sports Sci，2005，23:196.

[5] Léger L, Lambert J. A maximal multistage 20 m shuttle run test to predict VO2max[J]. Eur J Appl Physiol Occup Physiol，1982，49:1-12.

[6] Leger LA, Mercier D, Gadoury C, Lambert J. The multistage 20 meter shuttle run for aerobic fitness[J]. J Sports Sci，1988，6:93-101.

[7] 王翔,陈嵘,蔡秋,王健.用20-MST预测大学生最大吸氧量的研究[J].浙江体育科学,2007，29(3):111-113.

[8] Bland JM，Altman DG.Statistical methods for assessing agreement between two methods of clinical measurement [J].Lancet，1986，1(8476):307-310.

[9] Cooper SM,Bake JS,Tong RJ,Roberts E,Handford M.The repeatability and criterion validity of the 20 m multistage fitness test as a predictor of maximal oxygen uptake in active young men[J].Br J Spors Med ，2005，39:19.

[10] Aziza r,Chia MYH,Teh KC .Measured maximal oxygen uptake in a multi-stage shuttle test and treadmill-run test in trained athletes[J].J Sports Med Phys Fitness，2005，45:306-314.

TheValidityofEvaluationtotheAerobicEnduranceof20-MSTWithinUniversityStudents

ZHANG Min-qing

(PE Department, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The Bland-Altman analysis is one method optimized to evaluate the validity of measuring performance. By using this method, this study is to test the validity of evaluation to the aerobic endurance of multistage 20 meter shuttle run test (20-MST) with university students through a designed experiment. The results show that it is not fully comprehensive to use the related coefficient only in terms of evaluating aerobic endurance for 20-MST. This method, however, is still effective without the systemic lean. Based on the prediction built by the performance at the first testing, the equation of linear regression for the performance of the second testing is: Y = 1.995 + 0.879X (Y is the value of the second testing; X is the value of the first testing). R = 0.746, p lt; 0.01.

20-MST; Bland-Altman analysis; validity; evaluation

1004-3624(2013)02-0114-04

G804.21

A

2013-01-03

张敏青(1980-)，男，浙江天台人，讲师，研究方向：体育教学与管理、运动训练.