粒子的动力学模型的应用和强子的质量
2013-11-06张一方
张一方
(云南大学物理系,云南 昆明 650091)
0 引言
粒子物理和场论中的动力学研究长期以来一直是一个重要问题.仅在《Physical Review D》中2006年标题含动力学的论文就有68篇,2007年有59篇.Sannino等比较了不同夸克场散射振幅与手征动力学的关系[1].Jain等讨论了由一个任意弱长程吸引力经变分方法导致的动力学手征对称性破缺[2].Fraga等研究了纯SU(2)规范理论中退耦相变的Langevin动力学[3].Doff探讨了标准模型SU(3)LU(1)X推广的动力学对称性破缺和TeV能量标度[4].Hong等从弦论研究了重子的手征动力学[5].BABAR协作组研究了B介子衰变到p珋ph末态的衰变动力学[6].Dittrich等从Regge作用研究了线性化的动力学[7].Aharony等介绍了动力学超对称破缺的某些简单的弦模型[8].Antebi等构造了动力学超对称破缺的一个简单的SU(5)局域模型[9].基于粒子的动力学模型及其拉氏量和方程,笔者进行了某些数学研究,探讨了相关的应用,并定量讨论了强子质量.
1 拉氏量和动力学模型
粒子物理中的拉氏量,最广泛的是相互作用统一及其破缺的拉氏量[10].它们基本由三类组成:自由场及其自相互作用项、彼此相互作用项和质量项.非Abel规范理论具有严格的定域对称性,则规范场的质量一定是零.但一般粒子都有质量,这表示定域对称性被破坏,质量常常由相互作用导致.它包括旋量场ψ、标量场φ和矢量场Aμ等.ψ可以描述自旋为1/2的基态粒子(包括轻子、夸克、重子),方程是有相互作用的Dirac方程.而自旋为0的介子相应于标量场φ和Klein-Gordon(KG)方程.标量场也可以描述对称性破缺并获得质量的Higgs场,决定自旋相同的强子之间彼此的纵规律.无质量时其对应Goldstone粒子.矢量场Aμ描述矢介子,它是弱相互作用的中间矢量玻色子,或者夸克相互作用的胶子,质量为零时可以是光子,对应电磁相互作用.其对应自旋不同的粒子之间的横规律.
Weinberg-Salam弱电统一理论[10]的运动方程为:

SU(3)对称性的拉氏量已经包含在相互作用统一的拉氏量中.由后者可以导出动力学模型(DM)[11]及相应的各种公式,Higgs的拉氏量等.
动力学模型的拉氏量为[12]:
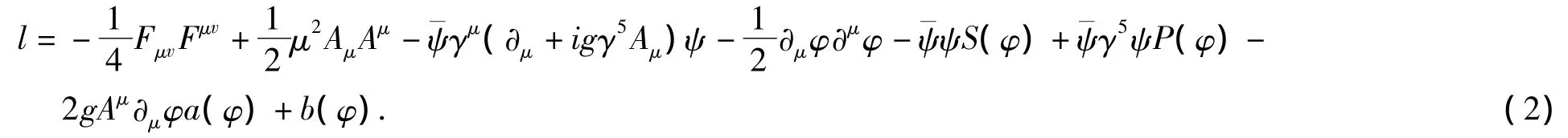
于是,运动方程为[12]:
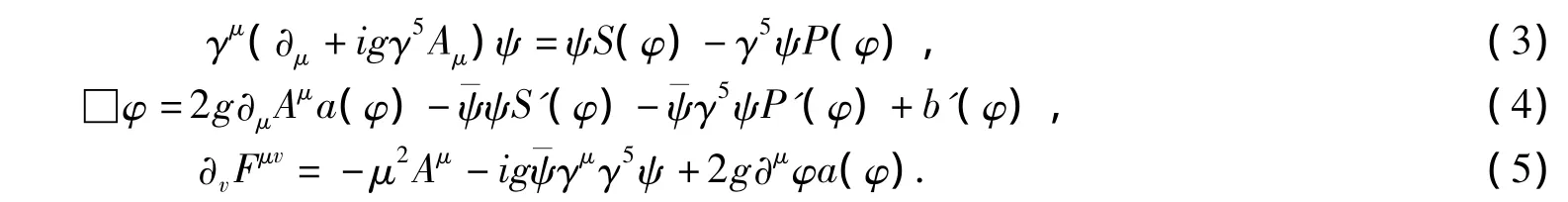
在动力学模型中,重子能级由ψ场方程导出,标量介子的能级由φ场方程导出,而矢量介子的能级由Aμ场方程导出.φ和Aμ场方程代入ψ场分别得到重子的纵、横规律:粒子规律表中的音阶谐振子和GMO质量公式及我们提出的对基态强子完全符合实验的修改的质量公式[11,13]:
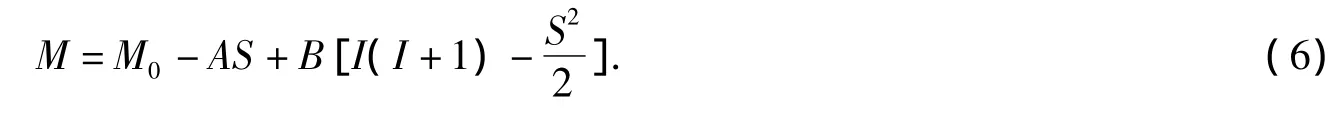
最近笔者由一般的具有振动和转动两种运动状态的突现弦(emergence string)方程就可以得到粒子的GMO质量公式及(6),并研究了对称的强子寿命公式[14].
φ场方程代入Aμ场方程是矢量介子的纵规律.Aμ场方程代入φ场方程得到标量介子的横规律.φ场导致对称性破缺,并由此获得质量.对φ-ψ场,Higgs破缺对称性时是孤子解,说明基态、纵规律稳定;对Aμ-ψ场则是类孤子解,说明共振态、横规律不稳定.各种具体机制的区别主要是φ和ψ场相互作用的具体形式.动力学模型符合SU(3)理论的结果,认为强子只是同一粒子的超多重态,仅仅量子数S、I不同而质量有所差异.
2 动力学模型的某些应用
ψ=Aμ=0时,简化后的动力学模型方程为[11]:

这与SLAC袋模型方程φ=4λ(φ2-f2)φ完全相同,其静态解为

方程可以再简化为□φ=0,这是一次近似,类似袋模型内部的场方程□φ=0,对应于Goldstone粒子.对球对称二维方程是

完全类似弦方程

Lorentz条件下,φ=0时,(5)化为


积分一次可得

积分常数C=B2/2μ2时,方程的解为
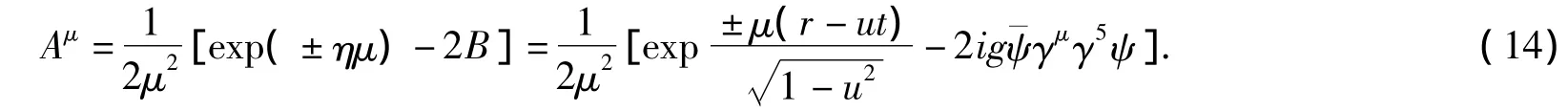
这种解不是波动方程型的Green解.但Aμ方程的精确解代入ψ方程(3),非相对论近似时也是Morse势和GMO公式及(6),取近似时化为谐振子势及其能级.
对称陀螺型的转动[15],能级是
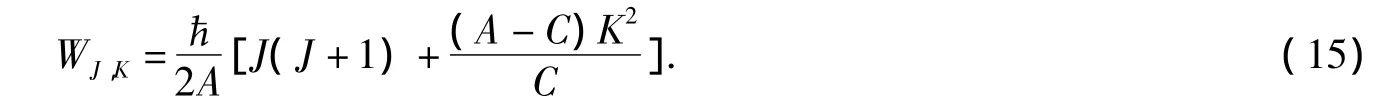
C=2A时与介子的推广的GMO公式[11]完全相同.相应的方程化为
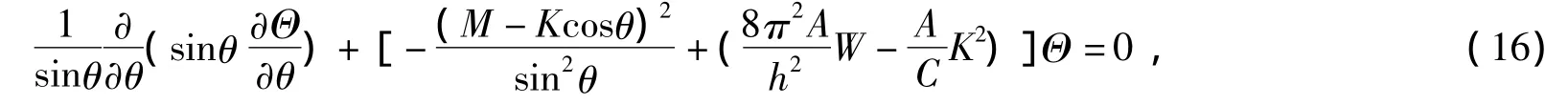
其解可以化为超比函数.进一步,由方程可以导出Goldstone超导解,Higgs涡线解(对应弦),又类似超导涡线.
3 动力学模型的若干具体结果
短程时标量场的解为
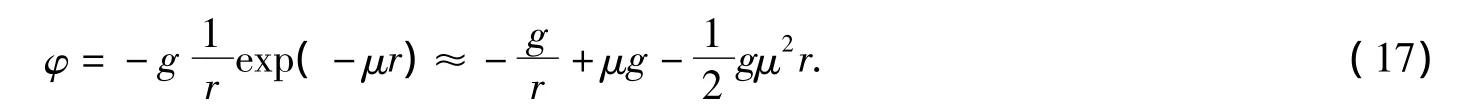
此势在r→0时为-∞,即斥力无穷大;在r比较大时为0,这表示短程相互作用.而近似解是电磁场的库仑势、常数势及弦势等之和.方程的孤子解和Green解统一.近似时各是库仑势φ∝1/r和弦势φ∝r.这联系于决定 ψ =c珋c 质量的唯象势[16,17]

后者是线性势,而前者联系于库仑势,所以此时电磁相互作用应该取一定作用.此势对应于夸克具有的渐近自由和红外奴役二重性.弦、袋等模型为此引入唯象的非线性自相互作用的Higgs标量场.粲素的非相对论势

也是符合QCD渐近自由的势,其中[18]V0= -0.76 GeV,αs=0.27,g=0.25 GeV,二者数值近似相等.(17)式中μ2=-2,则完全一致.
动力学模型可以简化为振动-转动模型[11,19,20],此时不同粒子是各种振动-转动能量的函数.它是把粒子内部特性的量子数归为一般时空或者特殊时空(如S-I或Q-U时空)的运动状态.介子质量公式的参数B为负说明转动使质量变小,这种反常似乎表明转动不是在一般的空间中.而一般弦也可以有振动-转动,由此导致相同的质量公式[14].
按照振动-转动模型,重子只有一个稳定的核心(质子p),其余只是外层不断增大的重子,至多是某些轨道比较稳定.而外围增大时通常更加不稳定,这应该是共振态寿命特别短的原因.SU(4)等夸克模型中必然存在udc等粲重子.如果二者统一,则粲重子就是轨道特别稳定的粒子.介子无稳定核心,它们经Ross公式稳定于μ子、电子e.粒子在基态低能时SU(3)符合最好,而高能激发态时,由于各种因素增多符合变差.一般而言,重子、介子的核心分别是p和π,它们分别对应于Dirac方程和KG方程.
动力学模型最后简化为谐振子模型时,质量公式近似等距.动力学弦是联系各种粒子的机制,是使粒子激发到各种振动-转动态的场,如此则更类似弦,而整个粒子结构类似袋.袋也导致Regge极.
已知Regge极S=AJ+B,我们曾提出对称的宽度公式Γ=aJ+b[11].二者结合可以得到公式
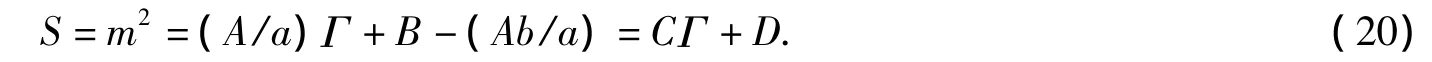
共振态的质量平方和宽度是线性关系.QCD等把渐近自由归为耦合常数,动力学模型是把其归为势.如此则与短程相互作用刚好相反,是一种特殊的相互作用.
质量公式(6)可以化为S、I完全对称的形式:

它实质上反映的是强子对称群的关系.按上述公式,对介子A=0,JPC=1--的 ρ,K*,ω,φ,由 m(ρ)=775.5=M0+2B和m(K*)=894=M0+B/4,可得参数B= -67.7和M0=910.9(S=0,I=0)≈[m(ω)+m(φ)]/2=(783+1019)/2=901.质量、寿命的精确公式必须包括二次项,也许只能作为微扰引入.
实际上,动力学模型只是讨论已知粒子之间的关系,特别是由动力学方程导致质量公式.这类似解Schrodinger方程导出氢原子的能级.最基本的粒子:质子p,电子e,它们的质量只能由基本参数决定,在Dirac方程中它们是给定的.而其它粒子的质量则由相互作用决定,如对标量场方程:
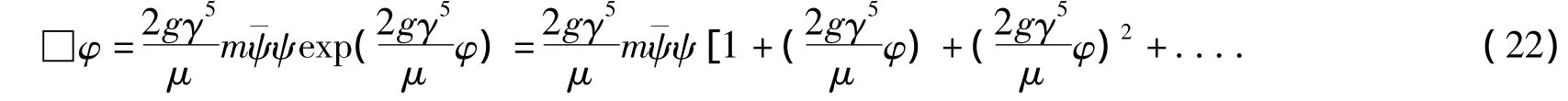
动力学模型中,Morse势为:

当r→∞时,U=D是常数,表示强相互作用是势阱.Morse势和谐振子势当r→r0时,都有U=0,这表示渐近自由,指出粒子在核心处无相互作用.
进一步,Morse势加谐振子势为:
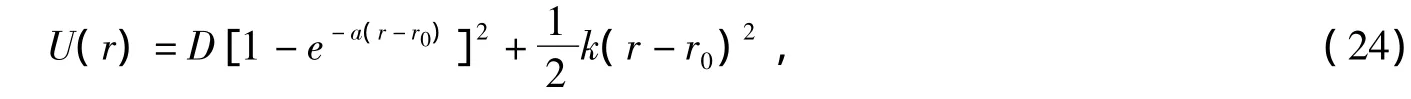
相应的方程为:
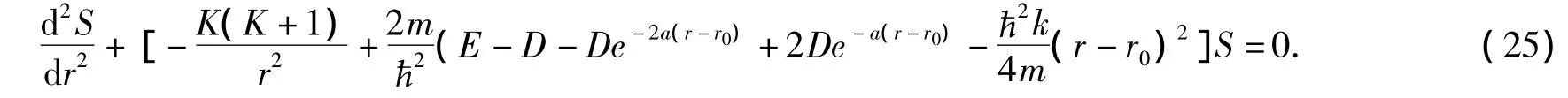
其能级近似为:
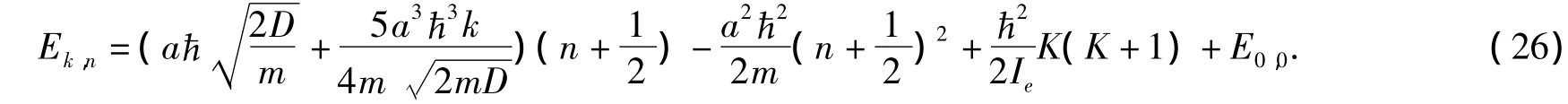
由上述能级可知,量子数n可以加不同系数,由此可以认为它们就是不同量子数,二者之比是.新量子数决定质量等距.它可能是C、B等量子数.
粒子结构本身及其量子数说明其具有振动-转动态.这一特性在实验中应该有所反映.动力学模型经拉氏量可以和很多模型互相结合.动力学模型应该随拉氏量及其方程发展.拉氏量有所不同时,许多结果仍然相同.这说明拉氏量具有一定的任意性,但其中又有统一性.拉氏量都包含相互作用.其中φ场的孤子解几乎都可以化为指数形式,其近似时正比于r.这说明表面神秘的类似性可能都是源于指数形式的短程相互作用.
一般假设对称性推广到SU(4)时出现新的量子数C.动力学模型推广到SU(4),可以认为是新的振动自由度,或者SU(4)时破缺不同,质量公式不同.动力学模型主要就是导出势,如Morse函数U(r)等.进一步,动力学模型及振动-转动模型也许可以应用于分子、原子核等理论中.
引入色的截面比R=σ(e+e-→h)/σ(e+e-→μ+μ-)和π0→γγ都是与夸克数、电荷有关.这类似磁矩与电荷有关.它们随能量E增高而变大,则部分子-夸克数N也应该随之增多,这样N是E的函数.动力学模型能量增大,方程及其破缺具有更大的对称性SU(3)→SU(4,5,6)等.但是无矢量场时,QCD的SU(n)方程、拉氏量都相同.能量不同,有新量子数C似乎可以归为破缺不同.动力学模型应该与MSM、统计模型相结合.统计方程与拉氏量结合.
QCD、拉氏量有所不同的主要是矢量场、胶子场及其相互作用项.当Aμ=0时,拉氏量为:

由此就可以得到Dirac方程.动力学模型中,动力学破缺对称性,再加标量场及其相互作用项.势V(r)代人Schrodinger方程:
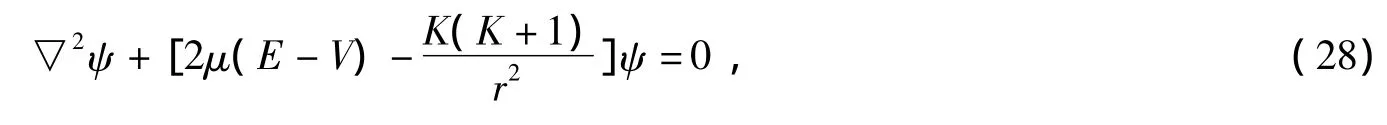
可以化为常微分方程:
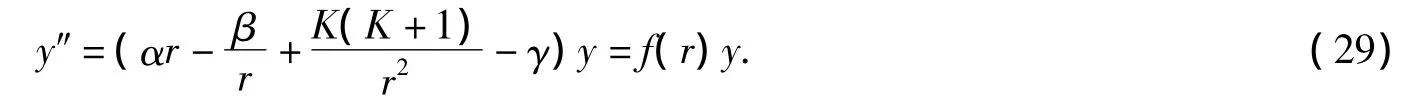
设y'=yu(x),得黎卡提方程:

欧勒型方程r2R″+rR'-n2R=0的解R=Crn+D/rn,n=1时即上述势(17)(18).
4 强子的质量
基态介子是π,K,η(JPC=0-+),它们的数目分别是3、2、1个,一共有6个粒子.
基态重子是N,Λ,Σ,Ξ(JP=(1/2)+),它们一共是8个粒子.对JP=(3/2)+的重子 Δ,Σ,Ξ,Ω,它们的数目分别是 4、3、2、1 个,一共有10 个.
对JP=(1/2)+的基态重子,N(939)跃迁到最低激发态(1/2)+的N(1445±25),质量差为506;跃迁到下一个激发态(3/2)-的N(1445±25),质量差为581.Λ(1115)跃迁到最低激发态(1/2)-的Λ(1406±4),质量差为291.Σ+(1189)跃迁到最低激发态(3/2)+的Σ+(1382),质量差为193.Ξ-(1321)跃迁到最低激发态(3/2)+的Ξ-(1535),质量差为214.对JP=(3/2)+的重子,Δ(1232)跃迁到最低激发态(1625±75),质量差为393.Ω(1672)跃迁到最低激发态(2252 ±9),质量差为580[21].它们的质量差之比近似为:5∶6∶3∶2∶2∶4∶6.
对JP=0-的基态介子,π(140)跃迁到最低激发态的介子η(548),质量差为408.K(496)跃迁到最低激发态(894),质量差为 398.对轻子,e(0.511)跃迁到下一个激发态 μ(105.658),质量差为 105[21].它们的质量差之比近似为:4∶4∶1.
Kunstmann等提出相对论自旋1/2粒子的基本质量量子[22].他们引入M=α-1me=70 MeV,m(μ)≈1.5 M=105 MeV,m(τ)≈ =25.5M=1785 MeV,对轻子是半整数.推广到介子是整数,m(π±)=2M=140 MeV,m(K±)≈7M=490 MeV,m(η)≈8M=560 MeV,m(D±)≈27M=1890 MeV.对重子是半整数,m(n)≈13.5 M=945 MeV.但 m(Λ)≈16M=1120 MeV.
笔者曾探讨过代的结构关系和重味强子的质量公式等[23].但随着重味强子的不断增多,其质量关系也越来越复杂.对重味夸克介子和族具有极好的对称性,都符合QCD,两方面基本类似[24].
5 动力学模型可能的发展
笔者探讨了粒子物理中的各种统一.它们包括相互作用统一和规范场,场、粒子及其方程的统一,低高能时的统一,统一和非线性理论的关系等.并且提出它们也许可以统一到统计性[25].粒子物理中一般的拉氏量必须包含五类场:ψB(重子,夸克)、ψL(轻子)、Aμ(超强相互作用的胶子,电磁相互作用的光子)、Bμ(弱相互作用的中间矢量玻色子)和φ(Higgs粒子,强相互作用介子)及各种场量的组合对应的各种粒子间的相互作用.这些就是相互作用统一的拉氏量及相应的群.
假设介子的核是轻子时,相应的方程是Dirac方程;附加旋量场导致振动,产生介子及相应的质量公式,再以此为核心形成振动-转动态的各介子.由此形成e→μ→π→其它介子的结构,定量的质量关系就是推广的 Rosen -Ross公式[11]m=me(1+n/2α).
动力学破缺的动力学模型的数学结果是唯一的,但其可以有不同的简化结果.进一步的发展可以联系于:(1)夸克、部分子模型,QCD假设夸克-胶子存在,其对称性破缺后是动力学模型,由此导出弦、袋等夸克幽禁的势;或者一开始就假设动力学破缺,夸克不一定存在;或者是幻夸克的MSSM[11].(2)动力学破缺是Higgs机制加鬼场.Higgs破缺导出粒子质量,鬼场对应Goldstone玻色子.(3)规范场及相互作用统一及其破缺,这联系于流代数、Higgs力学、Goldstone粒子等.(4)QCD、QFD,QCD对称性被Higgs机制或动力学破缺.(5)Regge极与Veneziano模型,包括胡宁等的谐振子理论[26],它们都统一在拉氏量及方程中.(6)双关模型及弦、袋等.(7)孤子、二维Sine-Gordon方程等价于Thirring模型.目前似乎主要只有统计模型及其碰撞理论还与此无关.
按照动力学模型基态粒子的各组成部分彼此接近,所以是弱相互作用及其衰变;而共振态横振动的各部分距离较远,所以是强相互作用及其衰变.对粒子的砂子-软物质(soft matter)模型,大量砂子构成粒子的软物质模型.由此可以对应粒子流体力学模型;流动的颗粒可以形成类孤子,这又对应夸克-部分子.这即砂子流动或运动时形成夸克.
按照振动-转动模型,粒子衰变应该有一个核.不同衰变道即从同一高激发态跃迁到不同的低激发态.这类似于原子的光子辐射.不同的光谱系对应于不同的衰变道.量子力学中的能量对应于衰变道、分支比中的宽度.不同类的衰变道类似不同类的光谱.衰变道可以由此结合统一的衰变公式[11].由此修改、发展及结合动力学模型的拉氏量有可能导致衰变及相应的流代数等.按照动力学模型基态粒子的各组成部分彼此接近,所以是弱相互作用及其衰变;而共振态横振动的各部分距离较远,所以是强相互作用及其衰变.由此修改、发展及结合动力学模型的拉氏量应可以导致衰变及相应的流代数等.
总之,对称性及其破缺已经由实验证实是粒子物理中一个极其重要的特性.其中动力学破缺应当是一个非常具有丰富内容的发展方向.
[1] Sannino F,Schechter J.Alternative large Nc schemes and chiral dynamics[J].Phys.Rev.,2007,D76(1):014014.1 -6.
[2] Jain B,Mitra I,Sharatchandra H S.Criterion for dynamical chiral symmetry breaking[J].Phys.Rev.,2007,D76(2):025020.1 -5.
[3] Fraga E S,Krein G,Mizher A J.Langevin dynamics of the pure SU(2)deconfining transition[J].Phys.Rev.,2007,D76(3):034501.1 -7.
[4] Doff A.Energy criterion and dynamical symmetry breaking in a extension of the standard model[J].Phys.Rev.,2007,D76(3):037701.1 -4.
[5] Hong D K,Rho M,Yee H -U,Yi P.Chiral dynamics of baryons from string theory[J].Phys.Rev.,2007,D76(6):061901.1-5.
[6] Aubert B,et al.BABAR Collaboration.Evidence for the Bdecays and study of the decay dynamics of B meson decays into pp final states[J].Phys.Rev.,2007,D76,092004.1 -18.
[7] Dittrich B,Freidel L,Speziale S.Linearized dynamics from the 4 - simplex Regge action[J].Phys.Rev.,2007,D76(10):104020.1 -15.
[8] Aharony O,Kachru S,Silverstein E.Simple stringy dynamical supersymmetry breaking[J].Phys.Rev.,2007,D76(12):126009.1 -6.
[9] Antebi Y E,Volansky T.Dynamical supersymmetry breaking from simple quivers[J].Phys.Rev.,2008,D77(2):026001.
[10] Weinberg S.The Quantum Theory of Fields[M].Cambridge University Press,1996.
[11] 张一方.粒子物理和相对论的新探索[M].昆明:云南科技出版社,1989.
[12] Jackiw R,Johnson K.Dynamical model of spontaneously broken gauge symmetries[J].Phys.Rev.,1973,D8(8):2386 -2398.
[13] Chang Yi- Fang.High energy behaviour of particles and unified statistics[J].Hadronic J,1984,7(5):1118 -1133.
[14] Chang Yi - Fang.From emergence string to mass formulas of hadrons and symmetric lifetime formulas of hadrons[J].International Review of Physics,2012,6(3):261 -268.
[15] 泡令 L,威耳孙 E.量子力学导论[M].陈洪生译.北京:科学出版社,1964.256.
[16] Appelquist T,DeRújula A,Politzer H D,Glashow S L.Spectroscopy of the new mesons[J].Phys.Rev.Lett.,1975,34(4):365-368.
[17] Eichten E,Gottfried K,Kinoshita T,et al.Spectrum of charmed quark - antiquark bound states[J].Phys.Rev.Lett.,1975,34(4):369-372.
[18] Novikov V A,Okun L B,Shifman M A,et al.Charmonium and gluons[J].Phys.Reports,1978,41(1):1 -133.
[19] 张一方.基本粒子的振动-转动模型和质量,寿命对称性[J].物理研究通讯,1979,1(2):26-31.
[20] 张一方.粒子的动力学模型和质量公式[J].吉首大学学报,2007,28(3):49-54.
[21] Nakamura K,et al.Particle Data Group[J].J.Phys.G.,2010,37(7A):075021.25 -88.
[22] Kunstmann O,Saavedra I.Basic mass quantum for relativistic spin -1/2 particles[J].Lett.Nuove Cim.,1985,43(2):108 -112.
[23] 张一方.代的结构关系,最简洁的粒子复合模型和重味强子的质量公式[J].云南大学学报,1994,16(2):100-105.
[24] 李政道.粒子物理和场论简引(下册)[M].北京:科学出版社,1984.166-171.
[25] 张一方.粒子和场方程的统一[J].商丘师范学院学报,2012,28(12):39-45.
[26] 胡宁,高崇寿,秦旦华,等.瞬时相互作用近似下介子结构波函数的一些探讨(II)[J].物理学报,1976,25(4):415-422.
