(2+1)维非线性薛定谔方程的线畸形波及其传播特性

楼吉辉，胡文成，赵辟，张解放2，

(1.浙江师范大学数理与信息工程学院，浙江金华321004;2.浙江传媒学院互联网与社会研究中心，浙江杭州310018)

(2+1)维非线性薛定谔方程的线畸形波及其传播特性

楼吉辉1，胡文成1，赵辟1，张解放2，1

(1.浙江师范大学数理与信息工程学院，浙江金华321004;2.浙江传媒学院互联网与社会研究中心，浙江杭州310018)

采用一个通用的理论，即用相似变换的方法，研究构建了(2+1)维非线性薛定谔方程的精确畸形波解，并进一步讨论了一阶、二阶光学畸形波的传输特性，我们提出的线畸形波概念在理论和应用方面都具有启迪价值.

(2+1)维;非线性薛定谔方程;相似变换;线畸形波

0 引言

畸形波首先是在海洋中[1－3]发现的，是一种目前尚无法全面解释和预测的突然出现的大浪，其波高明显大于甚至数倍于相邻波，波峰高而陡且常以单峰出现，存在时间很短[4].因其突发时的强危害性、目前的不可预测性及出现频次迅速增加的趋势，已经引起了全世界涉海工作人员的重视[5－7].一般而言，调制不稳定性(MI)被认为是畸形波产生的主要机制;另外孤子的碰撞，由于伴随着能量的交换，也会产生畸形波[8].目前畸形波动力学特征的物理模型大多采用非线性薛定谔方程来表征.自20世纪80年代以来，非线性薛定谔方程(NLSE)已成为非线性科学中一个重要的基本方程，它出现在很多领域中，如水动力学、非线性量子场论、等离子体物理、非线性光学、流体动力学等.几十年来不同学科的研究者用不同方法对非线性薛定谔方程(NLSE)的求解及其动力学行为进行了系统而全面的研究.在非线性光学中，非线性薛定谔方程可以很好地描述单模光纤中光孤子的传播行为，而且可以传播无限长的距离而不会有信息失真和波形畸变，具有很高的传输码率.鉴于不同物理图景都可以有非线性薛定谔方程描述，因此随着对畸形波研究的深入，相继在玻色－爱因斯坦凝聚[9－11]、非线性光学[12－13]等领域被开拓讨论.1995年畸形波在挪威开放海域的石油平台上被首次观测，其后在光学系统和玻色－爱因斯坦凝聚中，畸形波的实现也不断报道[10，14].

因为实际的物理问题都是高维的，本文旨在构建(2+1)维非线性薛定谔方程的精确畸波解，并进一步讨论线畸形波的传播特性.

1 (2+1)维非线性薛定谔方程精确畸形波解

(2+1)维常系数非线性薛定谔方程具有如下形式:

其中u(z，x，y)是光脉冲波包的电场强度分量，z是归一化后的传播距离，x和y是归一化后传播平面上的两个直角坐标分量.

为了研究光学畸形波的动力学特性，我们对方程(1)中的u进行相似变换:

其中，函数ρ(z)和φ(z，x，y)分别代表了解的振幅和相位，实函数X(z，x，y)是相似变量，关于归一化传播距离的实函数的Z(z)在这里代表有效传播距离.将方程(2)代入方程(1)，我们就可以得到复函数U(Z，X)将会满足常系数标准非线性薛定谔方程:

将相似变换(2)代入方程(1)的过程中，我们得到各变换系数函数必须满足的一组微分方程:

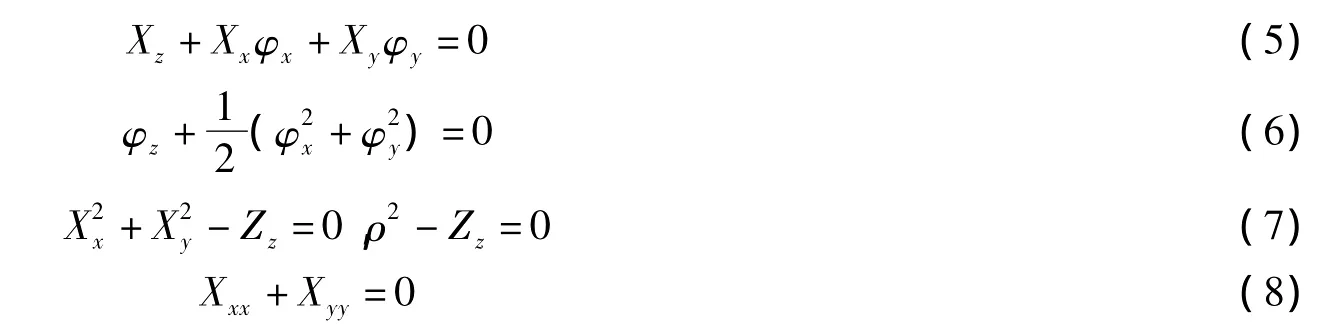
由方程(8)，我们不妨定义相似变量有如下的函数形式:

式中，k，l和p都是待定的关于传播距离的实函数，将方程(9)代入方程(5)可以得到:

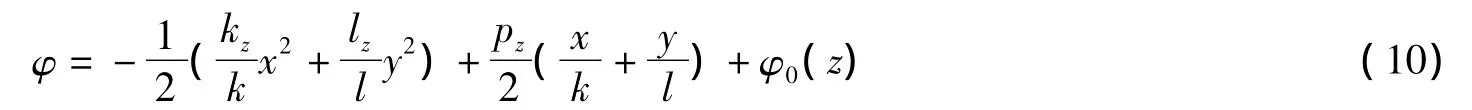
其中，φ0(z)，k(z)，l(z)和p(z)可以通过将方程(10)代入方程(6)得到.经代数运算后我们可以得到上述四个实函数有如下的函数形式:

式中，k0，l0，c0，c1，c2是实常数.这里需要说明的是c1同输入脉冲的初始啁啾参数有关.通过将方程(10)－(14)代入方程(4)和方程(7)，我们便得到了振幅ρ和有效传播距离Z的表达式:

我们之所以把方程(1)通过相似变换，化到方程(3)，是因为对于方程(3)学界已有诸多的解析解研究成果，诸如行波解、亮孤子解和暗孤子解和有理数解等等.这里，我们将考虑由D.H.Peregrine在1983年提出的振荡有理解[3].我们对其一阶解作伽利略变换[3，22]可以得到U(Z，X)具有如下的解的形式:

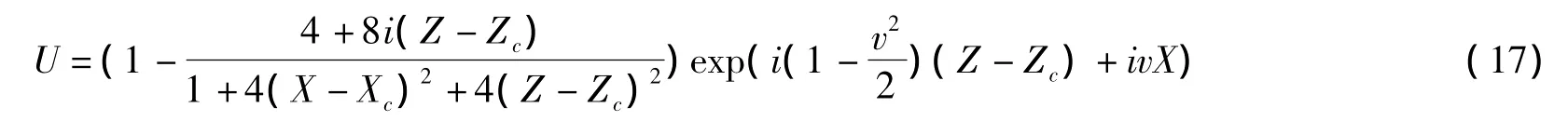
其中Zc和v是两个任意常数，Xc=v(Z－Zc)是畸形波的中心位置，Z=Zc是畸形波出现的位置.将方程(17)代入相似变换方程(2)，我们就可得到方程(1)的一阶振荡有理解:

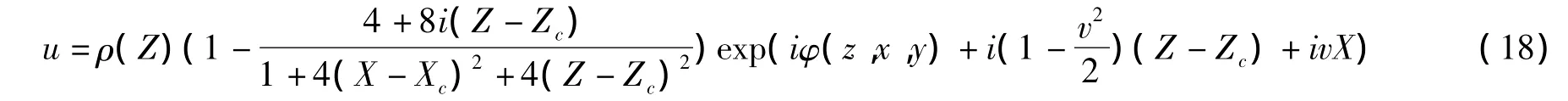
这个解我们称之为一阶二维光学畸形波解.因为方程(3)还存在更高阶的有理解，同样可以求出方程(1)的高阶二维光学畸形波解.方程(3)的二阶Peregrine孤子解是:

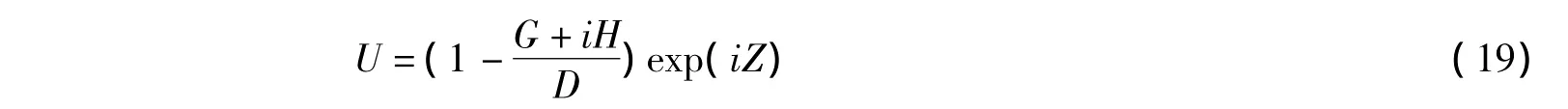
表达式中的G，H和D分别为:

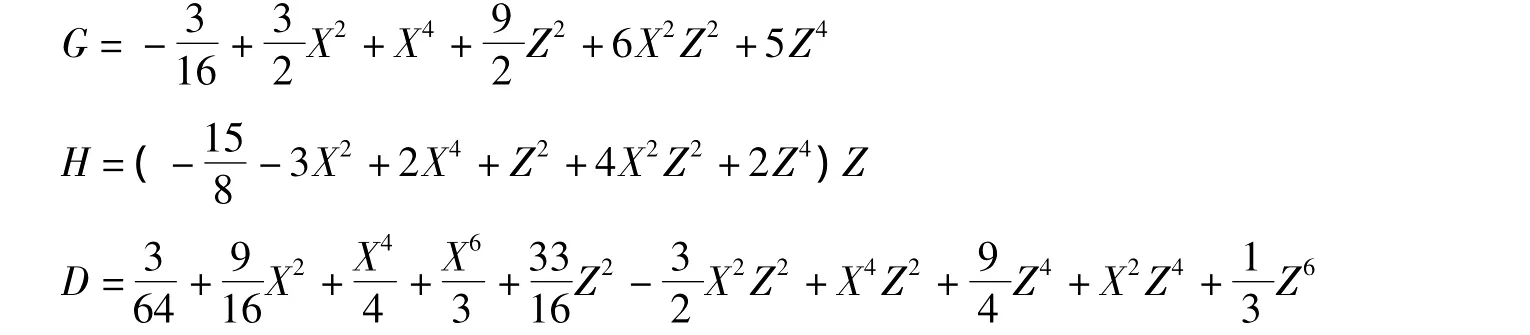
类似于一阶解的处理方式，对二阶Peregrine孤子解进行伽利略变换，可以求出方程(3)的二阶二维光学畸形波解:

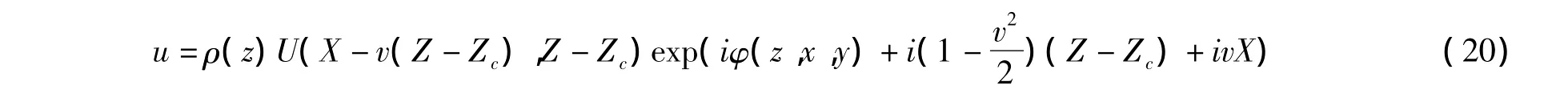
其中φ，φ，Z和X有方程(6)到(9)给出.

值得指出，这里得到的精确二维畸形波解(18)和(20)是关于线性组合坐标和传播距离表示的一阶和二阶二维有理形式解.但考虑到实际物理背景，只有在平面上讨论方程(1)的解才有意义，如光学上就是波导介质截面，水动力学就是水平面.在下节，类比于KP方程的线孤子解，我们在平面上研究(2+1)维非线性薛定谔方程的精确畸形波解，并分析其动力学传播特性.

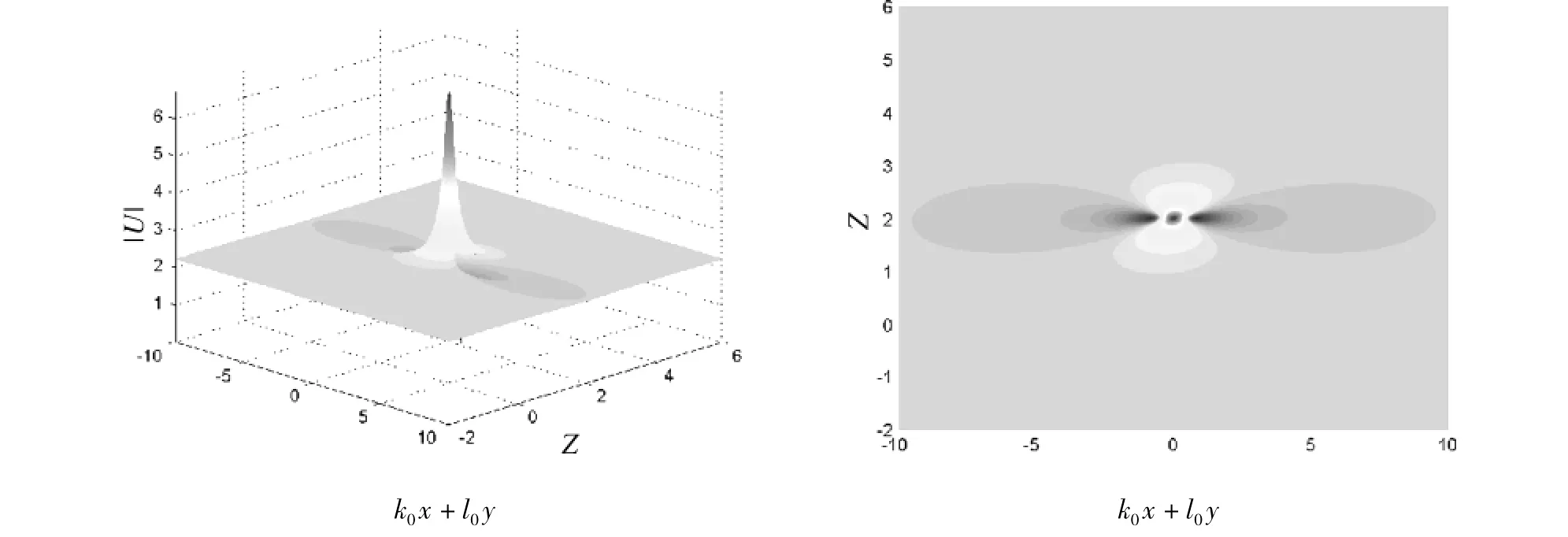
图1 1阶二维光学畸形波在线性且合坐和有效传播距离坐标上的图像.其参数为:k=2，l=1，c1=0，Zc=10，v=0.1，Z0=0

2 二维线畸形波的演化传输特性

下面我们将对无初始啁啾(c1=0)的二维光学畸形波的传输特性进行讨论.为简洁起见，令c0=1，Z0=0就有:

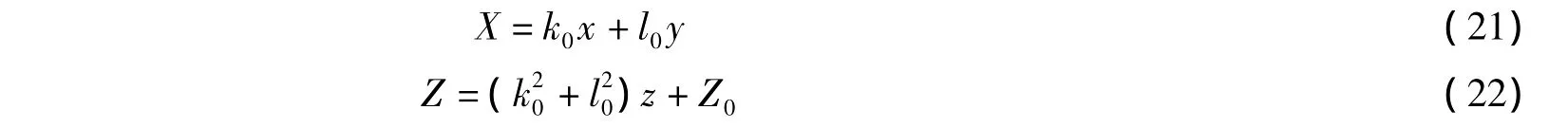
从方程(2)、(17)和(21)中，我们可以得到无啁啾光学脉冲的中心位置为Xc=v(Z－Zc).而且，从方程(22)中，可以看出此时有效传播距离Z是归一化传播距离z的一次函数.考虑到知道方程(1)中初始光脉冲u(z，x，y)的演化是由相似变换后方程(3)所描述的初始脉冲U(0，X)的演化决定的，我们可以知道这两者的演化是等价的.因此，如果Z＜Zc或Z＜Zc，则畸形波将不会被激发(将被抑制)，因为从方程(3)中可以看出畸形波在Z=Zc处才具有最大波幅.当然，我们也可以通过将方程(22)与方程(19)代入到解的表达式(17)中，来研究具有初始啁啾的光学畸形波，本文中限于篇幅不予讨论.

当Z=(k2+l2)z+Z0=Zc即z=(Zc－Z0)/(k2+l2)时，光脉冲的振幅迅速达到最大值，然后振幅迅速减小.

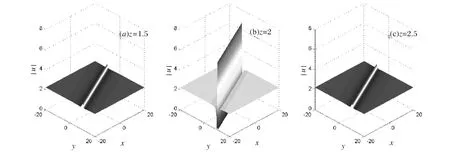
图2 1阶二维光学畸形波在x－y平面上随归一化传播距离z的演化图像(其参数同图1).

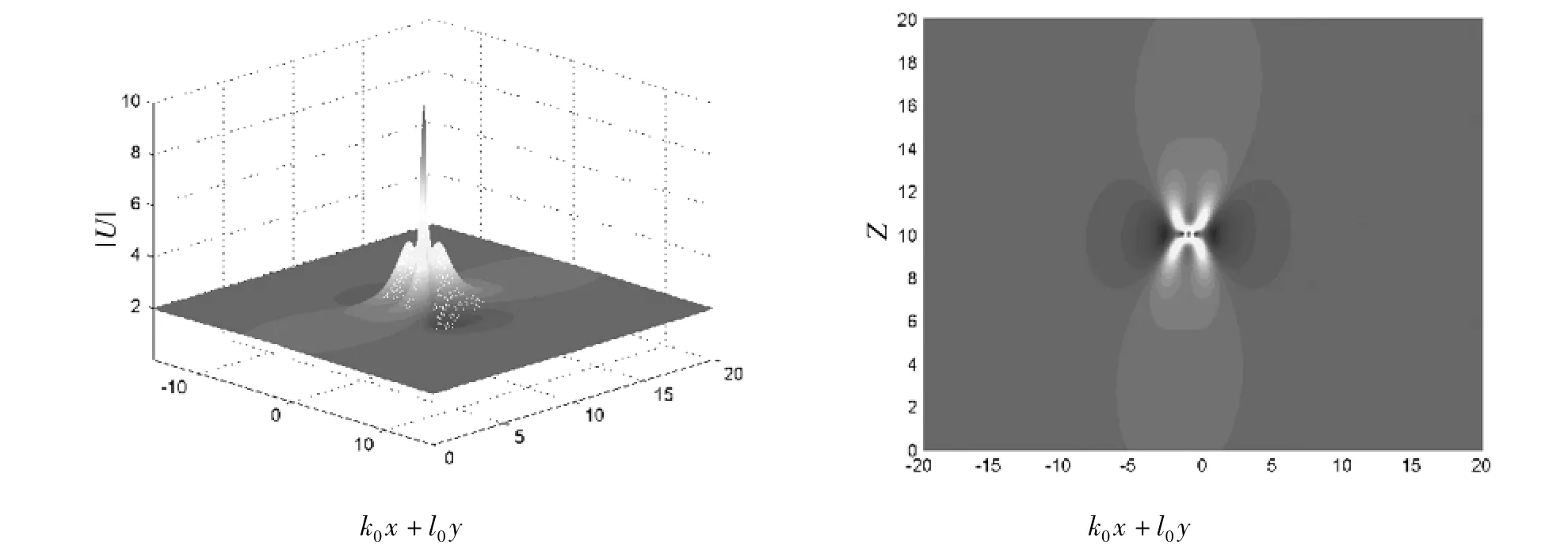
图3 2阶二维光学畸形波在线性组合坐标和有效传播距离坐标上的图像.其参数为:k=2，l=1，c1=0，Zc=10，v=0.1，Z0=0

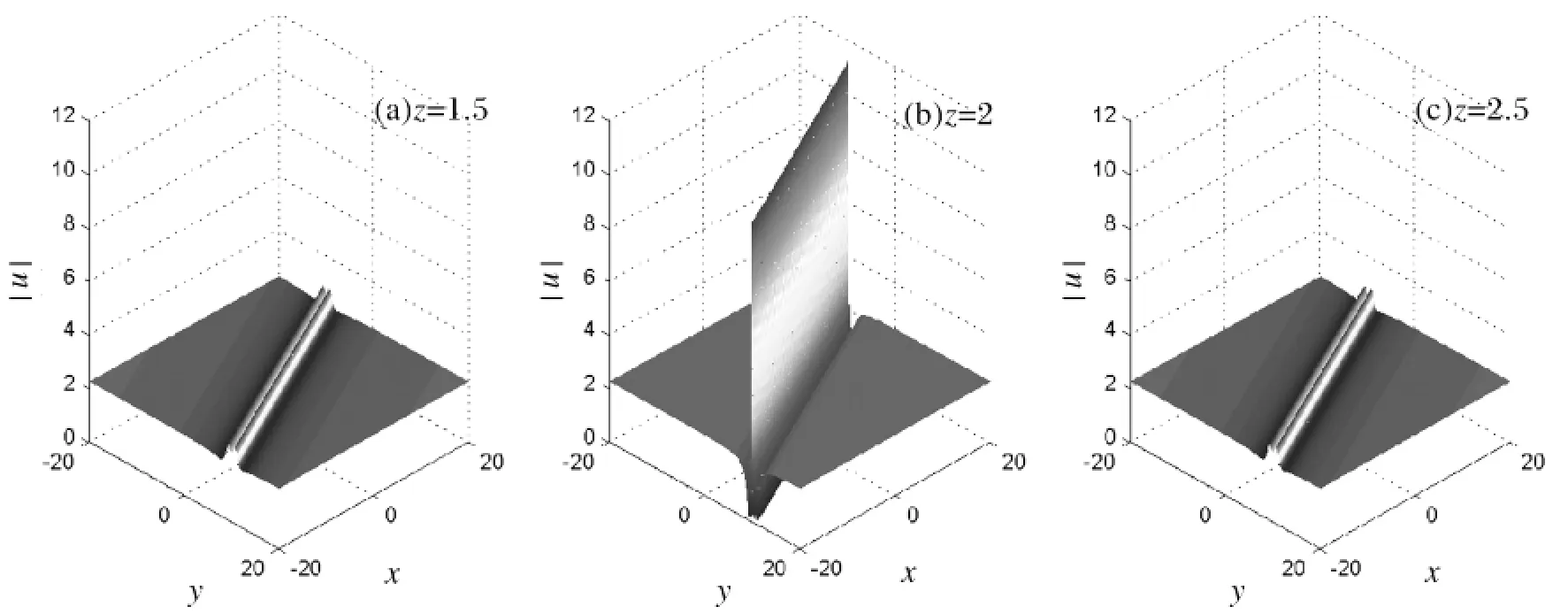
图4 2阶二维光学畸形波在x－y平面上随归一化传播距离z的演化图像(其参数同图1)

图1、图3分别为一阶二阶二维光学畸形波在线性组合坐标和有效传播距离坐标上的图像.图2、图4给出了对应的畸形波在真实的x－y平面上随归一化传播距离z的演化图像.可以看出，在真实的x－y平面上，二维畸形波呈现出线孤子的形态，但与孤子不同的是，其最大峰值极大，保持了畸形波的独有性质，所以我们可以称这样的波为线畸形波.

3 结语

总之，本文构建了(2+1)维非线性薛定谔方程精确畸形波解，即有理形式解，同时发现二维畸形波具有KP方程线孤子解的特征，因此我们提出了线畸形波的概念，并讨论了一阶、二阶线畸形波的传播特性.这些结果丰富了我们对畸形波的认识和了解.值得指出，本文的处理方法还可以用来降低维数，减少了研究高维问题的复杂性，这为讨论高维问题提供了一个有启迪的途径.

[1] Osborne Z R.Nonlinear Ocean Waves[M].Academic Press，New York，2009.

[2] Kharif C，Pelinovsky E，Slunyaev A.Rogue Waves in the Ocean，Observation，Theories and Modeling[M].Springer，New York，2009.

[3] Muller P，Garrett C，Osborne A.Rogue Waves:The Fourteenth'Aha Huliko'a Hawaiian Winter Workshop[J].Oceanography，2005，18:66.

[4] 陶爱峰，胡国栋.灾害性异常浪特性及研究方法综述[J].自然灾害学报，2008，17:01.

[5] Akhmediev N，Ankiewicz A，Taki M.Waves That Appear from Nowhere and Disappear without a Trace[J].Phys.Lett.A.，2009，373:675－678.

[6] Ankiewicz A，Devine N，Akhmediev N.Are rogue waves robust against perturbations[J].Phys.Lett.A.，2009，373 3997－4000.

[7] 李俊，陈刚，杨建民，深水畸形波的实验室物理模拟[J].中国海洋平台，2009，24:03.

[8] 谢涛，南撑峰，旷海兰，邹光辉，等.反常波海面参数计算方法及其色散关系[J].物理学报，2009，58:4001.

[9] Dalfovo F，Giorgini S，Pitaevskii L P，Stringari S.Theory of Bose－Einstein condensation in trapped gases[J].Rev.Mod.Phys.，1999，71:463－512.

[10] Bludov Y V，Konotop V V，Akhmedicv N.Matter rogue waves[J].Phys.Rev.A.，2009，80:033610.

[11] Liu W M，Wu B，Niu Q.Nonlinear Effects in Interference of Bose－Einstein Condensates[J].Phys.Rev.Lett.，2000，84:2294－2297.

[12] Ponomarenko S A，Agrawal G P.Nonlinear interaction of two or more similaritons in loss－and dispersion－managed fibers[J].J.Opt.Soc.Am.B.，2008，25:983－989.

[13] Tian Q，Yang Q，Dai C Q，Zhang J F.Controllable optical rogue waves:Recurrence，annihilation and sustainment[J].Opt.Commun.，2011，284:2222－2225.

[14] Solli D R，Ropers C，Koonath P，Jalal B.Optical rogue waves[J].Nature.，2007，450:1054－1057.

[15] Peregrine D H.Water waves，nonlinear Schrödinger equations and their solutions[J].J.Australian Math.Soc.Ser.B.，1983，25:16－43.

[16] Ohta Y，Yang J K.General high－order rogue waves and their dynamics in the nonlinear Schrödinger equation[J].Proc.R.Soc.A.，2012，468:1716－1740.

[17] Serkin V N，Hasegawa A.Novel Soliton Solutions of the Nonlinear Schrödinger Equation Model[J].Phys.Rev.Lett.，2000，85:4502.

[18] Ponomarenko S A，Agrawal G P.Interactions of chirped and chirp－free similaritons in optical fiber amplifiers[J].Opt.Express.，2007，15:2963－2973.

[19] Kruglov V I，Peacock A C，Dudley J M，Harvey J D.Self－similar propagation of high－power parabolic pulses in optical fiber amplifiers[J].Opt.Lett.，2000，25:1753－1755.

[20] Yan ZY.Nonautonomous“rogons”in the inhomogeneous nonlinear Schrödinger equation with variable coefficients[J].Phys.Lett.A.，2010，374:672－679.

[21] Moores J D.Nonlinear compression of chirped solitary waves with and without phase modulation[J].Opt.Lett.，1996，21:555–557.

[22] Dai C Q，Zhu S Q，Wang L L，Zhang J F.Exact spatial similaritons for the generalized(2+1)－dimensional nonlinear Schrödinger equation with distributed coefficients[J].Europhys.Lett.，2010，92:24005.

Line rogue wave solution of(2+1)dimensional nonlinear Schrödinger equation and its propagation characteristic

LOU Jihui1，HU Wencheng1，ZHAO Bi1，ZHANG Jiefang2，1
(1.Institute of Nonlinear Physics，Zhejiang Normal University，Jinhua 321004，China;2.Center of Internet and Society Zhejiang University of Media and Communications，Hangzhou 310018，China)

We propose a unified theory，that is similarity transformation，to construct exact optical rogue wave solutions of(2+1)dimensional nonlinear Schrödinger equation.Moreover，we investigate propagation dynamics of the first－order and second－order optical rogue wave in the optical fiber amplifier.Finally，we introduce the concept of linear rouge wave which will give edification in theory and practical application.

(2+1)－dimensions;similarity transformation;nonlinear Schrödinger equation;line rogue wave

O411.1

A

1672－3600(2013)06－0034－05

2013－03－19;

2013－04－15

国家自然科学基金资助项目(No.11072219)

楼吉辉(1987－)，男，浙江余姚人，浙江师范大学硕士研究生，主要从事非线性物理的研究.

张解放(1959－)，男，浙江义乌人，浙江传媒学院教授，博士，苏州大学兼职博士生导师，主要从事非线性波、光孤子动力学、复杂网络等方面的研究.

【责任编辑:徐明忠】