两类n阶本原有向图的广义competition指数

郝慧娥，高玉斌

(中北大学数学系，山西 太原 030051)

0 引言

近年来，基于非记忆通讯系统中信息传递的研究，M．Akelbek、柳伯濂等引入了scrambling指数及其广义scrambling指数．在文献［1］［2］中作者给出scrambling指数和广义scrambling指数的定义，文献［3］中，作者刻划了具有最大scrambling指数的本原有向图，文献［4］中，Hwa Kyung K im和Sung Gi P ark引入本原有向图的广义competition指数的定义，文献［4－8］得到了一些本原有向图的广义competition指数，并进行了极图刻画．本文将研究两类n阶本原有向图的广义competition指数．文章中所涉及到的符号表示的含义详见文献［4］［7］［8］．

定义1 设D是n阶本原有向图．如果存在正整数k，对D中任意顶点vi和vj，总存在w∈V(D)，这里w可能与vi，vj有关，使得从vi和vj到w都有k长途径，满足这样条件的最小正整数k称为n阶本原有向图D的scrambling指数，记作k(D)．

定义2 设D为n阶本原有向图，1≤m≤n，对于任意的顶点u，v∈V(D)，存在正整数m，在D中总能找到m个点，使得u，v到这m个点都存在k长途径，上述k的最小值称为D的m－competiiton指数，记作km(D)．m－competiiton．指数也称为广义competition指数．

定义3 设D是本原有向图，v∈V(D)，则RDt(v)表示有向图D中顶点v经过t长途径所能到达的顶点的集合，其中t为非负整数．

1 主要结论

定理 1 设 D1为 n(≥3)阶本原有向图，其顶点集 V(D1)={v1，v2，…，vn－1，vn}，边集 E(D1)={(vi，vi+1)|i=1，2，…，n － 1}∪{(vn－1，v1)，(vn－1，v2)，(vn，v2)}，则本原有向图 D1的广义 competition 指数 km

证明:设 C 是 n－2长圈，x，y∈V(D1)．由 D1的本原性可得是本原的，V)=V(D1)，E()={(vi，vi－1)|i=2，…，n}∪{(vi，vi)|i=2，3，…，n －1}∪{(v1，vn－1)，(v2，vn)}

Case 1 n+m 是偶数．

由本原有向图 D1可得V(C)，使得(x，vi)，(y，vj)∈E(D1)．在本原有向图中都是环点，从经过长途径所能到达的点的个数最少为同理．若从v，v至少有一个点经过ij长途径所能到达的点中包含v1，不妨设vi，则，故反之，则故从 vi，vj经过长途径所能到达的公共点的个数最小为m．因此，从而另一方面，对于长途径所能到达的公共点的个数小于m ，所以

Case 2 n+m是奇数．(1≤m≤n－1)

同理本原有向图 D1中∈V(C)，使得都是环点，从vi经过长途径所能到达的点的个数最少为同理．除环点外有且仅有两个n－1圈，故从经过长途径所能到达的公共点的个数最小为m．因此

定理得证．

定理 2 设 D2为 n(≥3)阶本原有向图，其顶点集，则本原有向图 D2的广义 competition 指数

证明:设 C1是 n－3长圈，C2是 n－2长圈．x，y∈V(D2)．

Case 1 n+m是偶数．

由本原有向图 D2可得∈V(C1)，使得(x，vi)，(y，vj)∈E(D2)．:

vi， vj都是环点，从 vi经过长途径所能到达的点的个数最少为同理，故从 v，v经过ij长途径所能到达的公共点的个数最小为m．因此，km(:vi，vj)≤，

从而km(D2:x，y)≤1+()(n－3)

另一方面，对于 v1，v[]∈V()，v1经过长途径所能到达的点集 {vn，vn－2，vn－3，…，}，经过长途径所能到达的点集 {，…，vn，v2，vn－1，v1，vn，vn－2，vn－3，…，}，从经过长途径所能到达的公共点的个数小于m，所以k(D:v，v)＞ ()(n－3)．m2ij

Case 2 n+m是奇数．

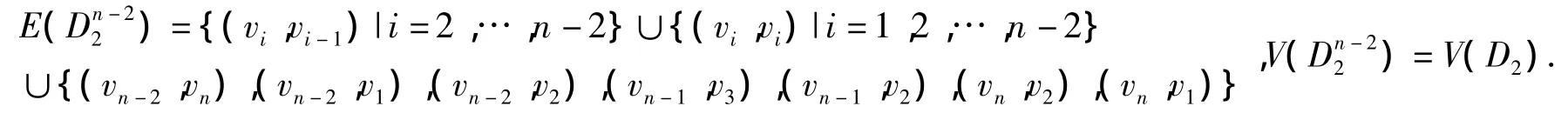
vi，vj都是环点，从 vi经过长途径所能到达的点的个数最少为同理包含一个n－3长圈，故从 vi，vj经过长途径所能到达的公共点的个数最小为 m．因此，km(:vi，vj)≤，从而k(D:x，y)≤1+()(n－2)m2

［1］ Mahmud Akelbek，Steve Kirkland ．Coefficients of ergodicity and the scrambling index［J］．Linear Algebra and its Applications，2009，430:1111 －1130．

［2］ Yufei Huang，Bolian Liu．Generalized scrambling indices of a primitive digraph［J］．Linear Algebra and its Applications，2010，433:1798－1808．

［3］ Mahmud Akelbek，Steve Kirkland ．Primitive digraphs with the largest scrambling index［J］．Linear Algebra and its Applications，2009，430:1109 －1110．

［4］ Hwa Kyung Kim．Generalized competition index of a primitive digraph［J］．Linear Algebra and its Applications，2010，433:72 －79．

［5］ Hwa Kyung Kim，Sung Gi Park．A bound of generalized competition index of a primitive digraph［J］．Linear Algebra and its Applications，2012，436:86 －98．

［6］ Min Soo Sim，Hwa Kyung Kim．On generalized competition index of a primitive tournament［J］．Discrete Mathematics，2011，311:2657－2662．

［7］ Hwa Kyung Kim．A bound on the generalized competition index of a primitive matrix using Boolean rank［J］．Linear Algebra and its Applications，2011，435:2166 －2174．

［8］ Hwa Kyung Kim，Sang Hoon Lee．Generalized competition indices of symmetric primitive digraphs［J］．Discrete Applied Mathematics，2010，160:1583 －1590．