一种改进的自补图构造方法

舒 涛 (四川民族学院网络信息中心，四川 康定 626001)

肖红德 (中科方德软件有限公司，北京 100190)

一种改进的自补图构造方法

舒 涛 (四川民族学院网络信息中心，四川 康定 626001)

肖红德 (中科方德软件有限公司，北京 100190)

现实世界中的交通网络、计算机网络等网络的模型构建都可以用图的构造方法来实现，研究满足某一性质图的构造方法具有十分重要的意义。提出了一种采用自补图标准型矩阵构造自补图的方法，并给出了具体实现算法。结果表明，利用该方法可以解决自补图构造过程中计算量过大的问题。

自补图；补图；标准型矩阵；算法优化

自补图是一种具有与其补图同构的特殊图，其计数问题在文献[1]中已有具体描述。而对于给定顶点数量时的所有不同构自补图的寻找问题，当顶点数为8和9的时候，很容易找到所有不同构自补图。实际上，要直接计算给定的2个图是否同构是一个非常困难问题，因为其计算量随着顶点规模的增加呈指数级增长[2]。下面，笔者在自补图计数理论[3]的基础上，给出了标准型矩阵的定义，这为判断一个图是否为自补图以及2个图是否同构提供了重要思路，并最终解决了同构图判定中计算量过大的问题。

1 图的标准型矩阵

图矩阵的标准型定义如下[4-5]：用和顶点数相等的阶数的方阵来表示自补图，0表示2顶点间无边相连，1表示2顶点间有边相连，并且矩阵的行和列所代表的顶点按照主对角线对称表示。把该矩阵的度序列按照由大到小的顺序排列，且度序列相等的行(若把一行从左到右看成一个整数的话)排在前面的比排在后面的大(或小)，所有符合这样的要求的矩阵中的最大(或最小)者。

上述定义的标准型矩阵为判断一个图是否为自补图以及是否为不同构的自补图提供了方便。因为对于一个给定的自补图，由整数的良序性质可知，其所对应的标准型矩阵是唯一的，通过对其标准型矩阵进行比较立即可以得出它们是否为不同构的自补图。另外，在判断一个图对应的矩阵是否为自补图的遍历方面也提供了方便。依据上述标准，只需对所有度序列相等的结点的顺序作全遍历即可，则要大大减少了遍历的次数，从而提高程序的执行效率。

2 4n阶和4n+1阶自补图的构造

2.14n阶自补图的构造

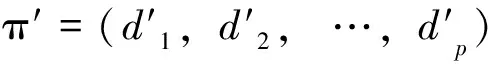
定理1一个单调递减的图序列π=(v1,v2,…,vp)是可自补度序列的充要条件π是相配的。

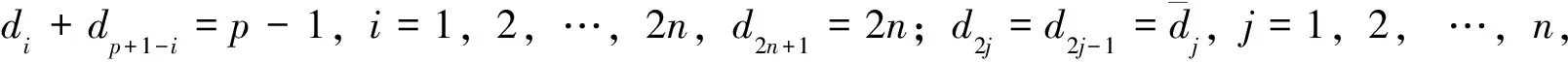
1)4n阶可自补度序列的构造 下面给出可自补度序列构造的步骤：

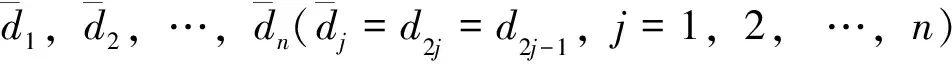
2)4n阶自补图的构造步骤 4n阶自补图的构造包括2个步骤，具体内容如下[6]。

Step1 构造4n阶的全部可自补度序列。

Step2 对每个可自补度序列，构造出与其对应的全部自补图，可按下列步骤完成：

(1)对每个可自补度序列，构造出与其对应的全部H(G的度数较小的前2n个顶点的导出子图)与H′(G的度数较大的后2n个顶点的导出子图)。

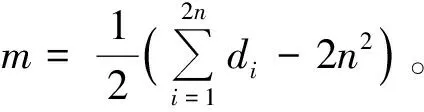
2.24n+1阶自补图的构造方法

定理4设G是一个4n+1阶的自补图，σ是G的一个自补置换，v∈V(G)且为σ的不动点(即σ(v)=v)，则G-v是一个4n阶的自补图。

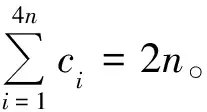
定理6设π*是一个4n维的可自补度序列，π是一个4n+1维的可自补度序列，并且π*可构造出π，则π*对应每个4n阶的自补图G*。通过增加一个度数为2n的顶点v与G*中的适当2n个顶点相连边，至少要产生一个4n+1阶的、度序列为π的自补图G。

应用定理4、定理5、定理6可以构造出所有4n+1阶的自补图，相关步骤如下。

Step1 按照4n阶可自补度序列的构造方法，从小到大求出4n+1维全部自补度序列。

Step2 写出全部4n阶可自补度序列，并按从小到大进行排列：

…

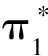
并且构造出相应的自补图。

Step3 对于每一个4n+1阶的可自补度序列π，构造出它所对应的所有自补图，相关步骤如下：

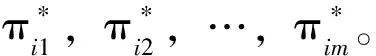
3 自补图的构造算法

3.14n阶自补图的构造算法

4n阶自补图的构造算法包括7个步骤，具体内容如下。

Step1 构造出4n阶自补图的度序列。

Step2 把自补图按照下列方法进行分解：先将自补图G的顶点按其度数的大小，从小到大进行排列v1,v2,…,v2n,…,v4n,然后令H=G[v1,v2,…,v2n]( 即G的度数较小的前2n个顶点的导出子图)，H′=G[v1,v2,…,v2n,…,v4n](即G的度数较大的后2n个顶点的导出子图)，再令H*=G-E(H)-E(H′)，于是有G=H+H′+H*。

Step3 构造H*(即所有2n阶补图，都为标准补图产生的矩阵)。

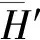
Step5 根据已经构造出来的H、H′和H*判断合起来的G是否为自补图，方法如下：把G及其补都化为标准型，然后判断其标准型是否相等，若相等，则可判断其为自补图，否则转至Step4。

Step6 若Step5产生的G是自补图，则将其加入到4n阶自补图的集合中去(若集合中存在该自补图，则不做任何操作，否则将其加入到自补图的集合中去)，转至Step4。

Step7 程序结束运行。

3.24n+1阶自补图的构造算法

4n+1阶自补图的构造算法包括9个步骤，具体内容如下。

Step1 构造4n+1阶行向量，其中含有2n个1和2n+1个0。

Step2 从4n阶自补图表中取出一个自补图。

Step3 把构造的4n+1阶行向量加入4n阶自补图的中间一行，并把4n+1阶行向量的转置加入到4n阶自补图的中间一列，构成4n+1阶矩阵。

Step4 把4n+1阶矩阵转换成标准型矩阵。

Step5 对标准型矩阵进行取反操作，即除主对角线以外，都进行取反操作(原来为1的变为0，原来为0的变为1)。

Step6 对Step5生成的4n+1阶矩阵进行标准化处理。

Step7 对Step4和Step6生成的矩阵进行比较，如果2个矩阵相等，说明该矩阵是4n+1阶自补图，转至Step8；否则，说明该矩阵不是4n+1阶自补图，转至Step9。

Step8 判断该4n+1阶自补图是否已经在4n+1阶自补图表中，如果已经存在，则不做任何操作，直接转至Step9；否则，把该4n+1阶自补图写入4n+1阶自补图表中，再转至Step9。

Step9 判断4n阶自补图表是否已经取完，如果没有，则转至Step2；否则，程序运行结束。

3.3算法运行结果

按照上述构造算法编写的程序，通过分别构造顶点数为8、9、12、13的不同构自补图，其得到的结果与理论计算一致。在硬件配置相同的计算机上，构造出13个顶点的所有5600个不同构自补图，采用文献[1]的方法编写的程序需要运行8d，而采用上述算法编写的程序则只需要1d，大大提高了计算速度，缩短了构造时间。

4 结语

自补图作为一种具有与其补图同构性质的特殊图，计算量大一直是构造自补图的主要问题。在分析前人给出的自补图计数理论的基础上，提出了一种通过构造标准型矩阵来判断一个图是否为自补图以及2个图是否同构的方法，采用该方法能够在很大程度上解决同构图判定中计算量过大的问题。今后，在构造程序的设计上还应继续研究采用集群或利用GPU加速的方法以进一步提高运算速度。

[1]Read R C. On the number of self-complementary graphs and digraphs[J].Lond Math Soc，1963 (38)：99-104.

[2] 许进.自补图理论及其应用[M].西安：西安电子科技大学出版社，2000.

[3]卜月华. 图论及其应用[M].南京：东南大学出版社，2000.

[4] 聂灵沼，丁石孙.代数学引论[M].第2版.北京：高等教育出版社，2000.

[5] 沈正梅. 探析同构图证明的新方法[J]. 常州工学院学报, 2007，20(1)：27-29.

[6] 李锋，李晓艳. 图的同构判定算法：关联序列法及其应用[J]. 复旦大学学报(自然科学版)，2001，40(3)：21-24.

[编辑] 李启栋

O157.5；TP393

A

1673-1409(2013)22-0006-03

2013-05-14

四川省教育厅一般项目(12ZB086)。

舒涛(1980-)，男，硕士，讲师，现主要从事计算机应用、计算机网络方面的教学与研究工作。