电力系统状态估计算法的综合分析

，，，

(西南交通大学 电气工程学院，四川 成都 610031)

电力系统状态估计算法的综合分析

古浩原，崔建强，杨浩，赵虎

(西南交通大学 电气工程学院，四川 成都 610031)

简要介绍了电力系统状态估计的基本概念及功能，描述了状态估计的数学模型。介绍了几种电力系统状态估计的基本算法，即加权最小二乘法、快速分解法、基于量测变换及逐次型的状态估计算法等，并对这些算法作了简明的对比，指出各个算法的优缺点。最后，为了满足电力系统状态估计的要求，又提出了几种新型的状态估计算法。并且指出了状态估计算法中值得研究的几个方面。

电力系统；状态估计；算法

1 引言

状态估计是当代电力系统能量管理系统(EMS)的重要组成部分，尤其在电力市场环境中发挥重要作用。而研究电力系统估计算法的目的在于找出好的算法，使之满足工程精度和响应速度要求的前提下，尽可能减少内存使用量，提高估计质量。对此，人们已经进行了大量的研究，提出了许多适于状态估计的计算方法。下面对常用的估计算法作简单的介绍并分析其各自的优缺点。

2 电力系统状态估计及其数学模型

2.1电力系统状态估计简介

状态估计是利用实时测量系统的冗余度来提高数据精度，自动排除随机干扰和噪声所引起的错误信息，估计或预报系统的运行状态。它是远动装置和数据库之间的重要一环，并能从远动装置接受低精度、不完整、少量的不良数据，而有状态估计后输出到数据库的是提高了精度，并且是完整而可靠的数据。状态估计功能流程图如图1所示。

图1 状态估计功能流程图

2.2状态估计的数学模型

2.2.1 量测模型

电力系统的量测量方程可表示为

z=h(x)+v

(1)

式中：z为量测量矢量；h(x)为量测量的计算值矢量；v为量测误差矢量；设量测量共m个，则上述矢量均为m维；x为状态量，设系统节点数为n，则x为维。

2.2.2 目标函数

给定量测矢量z以后，状态估计矢量x是满足如下的目标函数：

J(x)=[z-h(x)]TR-1[z-h(x)]

(2)

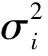
为了求状态估计值x，采用的迭代算法为：

Δx(l)=[HT(x(l))R-1HT(xl)]-1HT(x(l))R-1(z-h(x(1)))

x(l+1)=x(l)+Δx(l)

(3)

式中：H(x)=∂h(x)/∂x为量测方程的雅可比矩阵，l为迭代序号。

3 电力系统状态估计基本算法

状态估计算法是根据量测值求得最优状态估计值的计算方法，是状态估计程序的核心部分。而不同的状态估计算法会对电力系统状态估计程序的性能有很大的影响，所以下面对加权最小二乘法、快速分解法、量测变换法和逐次型算法作一下对比分析并指出各自的优缺点。

3.1基本加权最小二乘法

加权最小二乘估计法是在状态估计中应用最为广泛的方法之一。它的特点是模型简单，对正态分布的量测量具有良好的性能。

在给定的电力系统网络中，状态变量与量测数据之间存在这对应关系如式(1)所示。量测数据可以是节点注入功率、支路功率和支路电流，而状态量一般是指各节点的电压值和相位值。

式(1)中，由于量测量之间存在着非线性的关系，通常需要将其转换成在局部线性的关系，再通过其他的迭代计算方法求得满足需要的解向量。

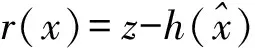
(4)

为使残差极小用下式进行表示：

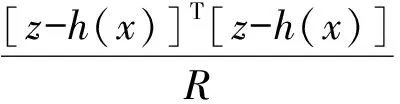
(5)

式中：R为量测量的误差方差矩阵。

对状态量在起始值为加处，进行一次泰勒展开，则有：

Δz=H(x0)Δx

(6)

由式(6)可推导出：

Δz=z-h(x0)

Δx=x-x0

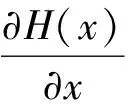
(7)

式(7)中H(x)为m×m阶雅克比矩阵。

那么，最终加权最小二乘状态估计算法的迭代计算如式(3)所示。

加权最小二成乘算法具有良好的收敛性能，而应用于大型电力系统则其计算时间长和所需内存大，所以受到一定的限制。

3.2快速分解法

快速分解法在基本加权最小二乘法的基础上，通过以下两种手段得出快速分解法状态估计的迭代修正公式，降低了问题的阶次，减少了雅克比矩阵的重复计算，大大的加快了潮流计算速度。

(1)有功和无功的分解：在高压电网中，正常运行条件下有功P和电压v、无功Q和电压相角θ之间联系很弱，反映在雅克比矩阵中∂P/∂V和∂Q/∂θ项接近于零。忽略掉这些元素就可以将P-θ和Q-v分开计算。由于降低了问题的阶次，既减少了内存的使用量，又可以提高每次迭代的计算速度，然而却要增加迭代次数。

(2) 雅克比矩阵常数化：一般来说，雅克比矩阵在迭代中仅有微小的变化，若作为常数处理仍能得到收敛的结果。利用常数化的雅克比矩阵就不必在每次迭代中重复对H和[HTR-1H]做分解了，仅利用第一次分解得到的因子表对不同的自由矢量前推和回代便可求其对应的状态修正量，因此可以大大提高迭代修正速度，然而迭代次数有所增加。

利用上述两项简化假设，推导出快速分解法状态估计的迭代修正公式：

[HT(x(l))R-1H(x(l))]Δx(l)=

HT(x(l))R-1(z-h(x(l)))

(8)

其中，状态量x分为电压相角θ和幅值v，同时雅克比矩阵对相角、幅值进行分解并简化，只要给出状态量初始值，经迭代就可以得到状态量的估计值。

快速分解法具有很好的收敛特性，既能处理支路上的量测量，又能处理节点注入型量测量，计算速度快而又节省内存，但却增加了迭代次数。

3.3基于量测变换的算法

在进行基本加权最小二乘法的状态估计中，状态估计迭代方程组的雅克比矩阵在每次迭代过程都须重新形成并重新因子化，因此算法的效率较低，无法满足电力系统实时在线的要求。量测变换状态估计算法在进行状态估计计算时所需的原始信息仅仅包含支路潮流量测量，假设运行电压变化不大，信息矩阵为常实数、对称的稀疏矩阵。该算法计算速度快，节省内存，但难以处理注入型测量量。

所以，把支路潮流量测变换为节点电压差的“量测”，与基本加权最小二乘状态估计器相似，可获得以下的迭代方程:

线路i侧量测变换

线路j侧量测变换

(9)

变压器i侧量测变换

变压器j侧量测变换

(10)

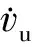
3.4基于卡尔曼滤波的逐次型算法

卡尔曼滤波是一种具有广泛用途的对系统运动规律进行回归及预测方对于量测集合{zi}，依次追加其中的量测量，则估计器的第j次迭代方程为：

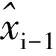
(11)

式中：h，H分别量测函数和雅可比矩阵，k分别为估计误差的协方差对角阵和增益系数，σ2和μ分别为量测误差方差和调谐参数。

上述迭代计算过程中，每追加一个量测值就需要进行一次迭代计算，在完成所有的量测量追加后，如果迭代尚未收敛且迭代次数没达到限制，则重新对量测量逐次追加并迭代。调谐参数通常取0.1～1.0之间的值。

逐次次型算法使用内存最少，对结点注入型量测量具有一定的适应能力，程序简单。其缺点是收敛速度慢，计算时间长，估计质量差，随着电力系统规模增大和结点注入型量测量的增多而变得更加严重，这些缺点限制了它的推广应用。

4 电力系统状态估计新型算法

随着电力系统的发展，区域电网互联，电力系统的规模不断扩大，结构和运行方式日趋复杂。电力市场化使电力系统运行必须同时兼顾安全性和经济性，而电力系统运行点越来越接近其极限条件，系统行为的不可预知性增大。这些新的形式对电力系统状态估计提出了更高的要求。所以，近几年来出现了几种新型的状态估计算法来满足电力系统更高的要求。下面将分析几种新型算法及其优点。

4.1抗差最小二乘法

目前抗差最小二乘法已经形成了一套完整的理论体系。抗差最小二乘法常用的几种误差分布为：(1)正态分布；(2) Laplace 分布；(3)Huber 分布；(4)混合正态分布；(5)有界分布。其他的分布还有柯西分布、伽玛分布、t分布、F分布。抗差最小二乘法的抗差实质体现在等价权的选择上。现有的选择不同等价权的抗差方法有：Tukey 双权法、Huber 法、Hampel 估计法、Andrews 正弦法、IGG 法。

抗差最小二乘法是在加权最小二乘法的基础上通过计算得出，主要体现在变权上。Huber分布的抗差最小二乘法的计算公式为：

(12)

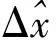
目前很多其他的抗差最小二乘方法基本上都是在现有的几种方法上进行改进，或者综合现有几种方法的优缺点的综合算法。抗差最小二乘法具有抗差性能好，收敛速度快，实时性好，算式简单等优点，能使抗差、状态估计在计算中一次完成。

4.2基于PMU的状态估计算法

随着相量测量算法的成熟和高速数字信号处理器的出现，PMU 的研制已经具备了软硬件条件，现在国内外都有了产品化的PMU 装置并在电网中投入使用，而PMU是在GPS同步下测量电网节点电压相量和支路电流相量的装置。

由于采用了精确的同步时钟、高速的处理器和通讯网络、有效的计算方法和抗干扰措施等，PMU量测具有如下特点：(l)相角量测精度满足工程实用要求。GPS同步精度在2ns内，相角量测精度可达到0.1度，能满足电力系统分析和控制对数据同步的要求。(2)数据带有精确时标，不同地点PMU数据能严格同步。电网状态量的直接量测。在直角坐标下量测量(包括电压和电流相量量测)与状态量呈线性关系。(3)数据更新周期短，传输速度快，能跟踪系统动态变化。美国BPA报道，运行中PMU每秒钟传送30个相量信息，即传输间隔可以达到30ms。(4)PMU提供的是当前系统状态及历史状态，不可能提供精确的未来系统状态。(5)PMU直接测量的是节点电压和线路电流相量，发电机功角必须采用其他的测量方法。

因此，文献[5]提出了基于电网部分电压相量和电流相量可测量的条件下，并且系统结构和参数己知，推导出了整个系统电压相量的线性状态估计表达式。文献[6,7]将PMU 量测及其直接计算值作为这些节点的状态估计值，可降低估计的规模和计算量。文献[8]提出了在传统SCADA 的基础上增加PMU 电压幅值和相角测量进行非线性估计。文献[9]提出通过量测变换来计及PMU 支路电流幅值和相角量测的模型，仿真说明该模型具有很高的估计精度。文献[10]在等效电流量测变换状态估计模型的基础上引入旋转变换，不需对电压的相角和幅值及有功和无功的量测权重作出任何假设，即可实现法方程的实、虚部严格解藕。同时，该模型可以充分利用PMU量测信息，其中包括支路电流相量量测，以提高量测冗余度。因此该方法所需的存储量较小、计算速度快和计算精度较高。总之，计及PMU 的状态估计算法是电力系统状态估计的一个重要研究方向。

4.3基于量测不确定度的状态估计

测量不确定度反映了可能的误差分布范围，可以近似地理解为一定置信概率下的误差限值。测量不确定度分为2类：标准不确定度和扩展不确定度。测量不确定度被国际化组织(ISO)定义为与测量结果相关联的参数，表征合理赋予的被测量之值的分散性。

测量不确定度表明赋予被测量之值的分散性，是通过对测量过程的分析和评定得出一个以测量值为中心的区间；测量不确定度与人们对被测量、影响量以及测量过程的认识有关，合理赋予被测量的任一个值，均具有相同的测量不确定度。文献[11]基于测量不确定度理论，提出了测点正常率概念，证明了测点正常率较大的状态估计结果更具合理性。给出了衡量状态估计结果合理性的具体方法。文献[12]是基于正常测点概念构造了相应测点评价函数，用于评价测点是正常测点还是异常测点；在此基础上，提出了以测点正常率最大为目标函数的状态估计新模型。该方法具有以下特点:(1)所求得状态估计结果的测点正常率较高；(2)可自动对不良数据点进行辨识；估计准确性不易受不良数据影响，具有很强的抗差性(3)所求得状态估计结果为潮流解，且满足各种物理约束，更加接近实际；(4)计算中无需进行不良数据检验、权重因子设置，调试和维护极为简单；(5)求解算法为现代内点法，收敛性好，计算速度快。

5 总结

本文介绍了电力系统状态估计的基本算法及其在每个算法中存在的优缺点，通过研究分析可以知道电力系统状态估计的基本算法已经不能满足电力系统的要求，所以，为了提高状态估计的准确性，研究出了几种新型的算法。当然，状态估计算法仍有许多问题需要深入研究：(1)基于GPS 相位角量测的PMU 技术应用于实时状态估计算法的研究；(2)面向大系统，开发计算速度快和数值稳定性好的算法，缩短状态估计执行周期；(3)抗差估计理论应用于状态估计算法进一步研究；(4)各种类型和多个相关坏数据条件下，状态估计算法的研究。

[1] 于尔铿.电力系统状态估计[M].北京:水利电力出版社,1985.

[2] 黄彦全.电力系统状态估计若干问题的研究[D].成都：西南交通大学,2005.

[3] 李碧君,薛禹胜,顾锦汉,等.电力系统状态估计问题的研究现状和展望[J].电力系统自动化,1998,22(11):53-60.

[4] 李响,刘玲群,等.抗差最小二乘状态估计[J].继电器,2003,31(7):50-53.

[5] 卢志刚,许世范,等.部分电压和电流相量可测量是电压相量的状态估计[J].电力系统自动化,2000,24(1):42-44.

[6] 王勇.基于相角测量技术的状态估计研究[D].南京:河海大学,2001.

[7] 刘怡.GPS 功角量侧在电力系统状态估计中的应用[D].北京:华北电力大学,2002.

[8] 赵红嘎,薛禹胜,等.计及PMU 支路电流相量的状态估计模型[J].电力系统自动化,2004，28(17):37-40.

[9] 孙国强.基于相量测量的电力系统状态估计研究[D].南京:河海大学,2005.

[10] 何广宇,董树蜂.基于测量不确定度的电力系统状态估计(一)[J].电力系统自动化,2009,33.

[11] 何广宇,董树蜂.基于测量不确定度的电力系统状态估计(二)[J].电力系统自动化,2009,33.

[12] 何广宇,董树蜂.基于测量不确定度的电力系统状态估计(三)[J].电力系统自动化,2009,33.

2013-02-26

古浩原(1987-)男，硕士研究生，研究方向为微机保护及变电站综合自动化；

崔建强(1984-)，男，硕士研究生，研究方向为微机保护及变电站综合自动化；

杨浩(1986-)，男，硕士研究生，研究方向为微机保护及变电站综合自动化；

赵虎(1986-)，男，硕士研究生，研究方向为高压绝缘。

IntegratedAnalysisofStateEstimatingMethodofPowerSystems

GUHao-yuan,CUIJian-qiang,YANGHao,ZHAOHu

(School of Electrical Engineering,Southwest University,Chengdu 610031,China)

The fundamental concept and function of power system state estimation are offered briefly and the mathematical model of state estimation is described.Some usual algorithms of state estimation are offered and compared briefly,such as recursive least square algorithm,fast decoupled method,state estimation method based on measurement transformation,etc.Then the advantages and disadvantages of each algorithm are pointed out.Finally,in order to satisfy the requirements of power system state estimation,and put forward some new types of state estimation algorithm is proposed.And the state estimation algorithm is worth study in several aspects.

power system；state estimation；algorithm

1004-289X(2013)06-0011-05

TM71

B