基于无模型自适应控制的温度控制系统设计

(湖北文理学院物理与电子工程学院，湖北 襄阳 441053)

基于无模型自适应控制的温度控制系统设计

陈铭

(湖北文理学院物理与电子工程学院，湖北 襄阳 441053)

分析了温度控制系统的动态过程特点和无模型自适应控制思想的本质，采用无模型自适应控制的思想，构造了相应的控制器。在模拟温度控制系统的过程中，分析了该系统的非线性、滞后性、时变性等特点，在温度加热和冷却控制过程中，借用PWM控制的思想，有效克服了采样间隔时间过长而导致加热时间或者冷却时间过长而引起温度波动较大的问题。仿真结果表明，基于无模型自适应控制的温度控制系统不仅具有较短的上升时间，而且抗干扰能力也较强，温度的稳定效果较好。

无模型自适应控制； 温度控制； 经典PID控制器

1 引言

温度变量是过程控制系统中的重要变量之一，该变量对产品的质量起着至关重要的作用。经典PID控制器由于其算法简单、鲁棒性好及可靠性高等优点，在可以建立精确数学模型的过程控制和运动控制领域中[1]，不仅得到了广泛的应用，而且获得了良好的控制效果[2]，该文明确指出经典PID控制器是一种标准的无模型控制器，但由于缺乏自学习能力，不具备对结构变化的适应性，故当被控对象或者控制系统的参数在使用过程中，不断变化时，基于传统控制理论设计方法设计的经典PID控制器很难获得满意的动态性能。这种情况不仅影响了控制效果，而且影响了产品质量和产量，最重要的是有可能影响生产安全性[3]。

为了克服温度控制系统的非线性、滞后性、时变性等特点，将人工智能的设计方法引入到温度控制系统的PID控制器的设计过程中，但由于其PID参数一经整定后，在控制过程中不再跟随系统参数的变化而变化，而当被控系统参数发生变化时，很难获得理想的控制效果。而无模型自适应控制结合经典PID控制的策略和现代人工智能中径向基函数神经网络的计算方法，既不建立也不辨识系统的数学模型[4]，也没有任何规则可供参考，充分利用系统的输入输出信息，计算新的控制变量控制系统，因此无模型自适应控制(MFAC)被称为是基于信息的控制，实际上是一种自适应的控制策略。

本文首先分析了温度控制系统和无模型自适应控制的特点，设计了相应的温度控制器，该控制策略不仅对其它的过程控制有着借鉴意义，同时也对其它的非线性系统的控制有着重要意义。

2 温度控制系统的特点分析

温度控制系统大体分为两类系统，一类系统从外部吸收热量；另一类系统内部产生热量，向外部释放热量[3]。从外部吸收能量的温控系统又分为恒温控制和匀速升温控制两类[5]。本文讨论的是第一种从外部吸收能量的恒温控制系统。

该温度控制系统是一个特殊的加热设备，电热丝在温控箱内部，电热丝温度很高，流通的空气把热量从电热丝上带走，加热被加热物质。从输入加热控制信号到温控箱内空气温度升高，中间经过电热丝加热和空气流动的通道，形成两个大的储热环节，从而构成一个二阶系统，由于电流的变化引起电热丝的温度变化，电热丝的温度变化引起空气温度的变化，需要一个滞后时间，这是一个具有滞后的二阶系统。当输入输出变量稳定后，该温度控制系统的动态过程可以用式(1)表示：

T2(t)=α1T1(t)+α0T0(t)+b1u(t-τ)+n(t)

(1)

其中:T2是当前被加热物体附近的空气的实测温度;T1是电热丝处的空气温度;T0是电热丝的温度;α1、α0是各自的温度传递系数;u是输入变量;b1是输入信号转化为温度的系数;τ是滞后时间;n(t)是电网电压波动以及其他不可测量的干扰信号。

由于温度控制系统中被加热物质本身的热容随物质大小、材料、形状的变化而变化，又由于温度控制系统本身具有非线性、时滞性和时变性等特点，故无论控制作用如何，在滞后时间阶段，控制信号对输出过程变量的影响是不可测的。同时，时间滞后导致了输出过程变量不能迅速地响应控制信号。在滞后时间阶段控制器由于得不到合适的反馈信号而进行的计算新的输出控制信号控制执行器，从而导致系统响应超调大甚至使系统失控。对于具有这些特点的温度控制系统，将无法确切描述该系统的数学模型和根据经典控制理论设计出合适的PID控制器，即使经过简化温度控制系统的动态过程，写出了数学模型，并且设计出了PID参数，由于这些参数不能随系统的变化而变化，故当系统的参数发生变化时，尤其是当我们对温度控制系统的超调量具有较高要求时，无法获得满意的控制效果。在这种情况下，无模型自适应控制应用径向基函数的神经网络计算系统的输入和输出信息，实时评估温度控制系统的控制性能，能够计算出最优的控制变量数0值。

3 无模型自适应控制系统

单回路无模型自适应闭环控制系统的方框图如图1所示，该控制系统包括一个执行器，一个无模型自适应控制器即MFA控制器和一个反馈检测装置。图中y(t)是该系统的输出信号，b(t)是系统的指令信号，e(t)是该系统地反馈信号，n(t)是误差信号，是系统的干扰信号。

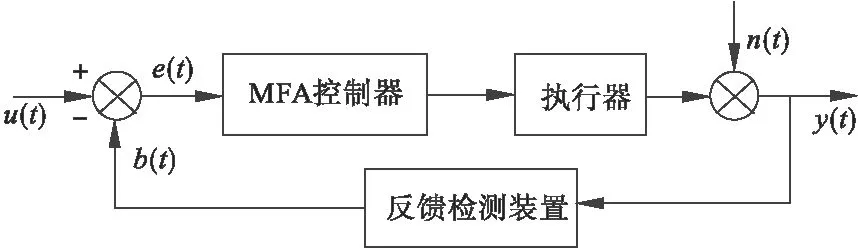
图1 MFA闭环控制系统方框图

4 无模型自适应控制器设计

一般情况下，单输入单输出系统的离散动力学方程可由式(2)描述：

y(k+1)=f(y(k),y(k-1),…,y(k-m),u(k),u(k-1),…,u(k-n))

(2)

其中，y(·)、u(·)分别表示系统的输出和输入，m和n分别表示系统输出和输入的阶数。

由温度控制系统的本质可以看出，该系统完全满足无模型自适应控制系统的3个假设条件：①系统是可观测的和可控的；②系统对输入信号都存在连续的偏导数；③系统是广义Lipschitz的[6-9]，那么必然存在一个伪偏导数φ(k)，即当Δu(k)≠0时，式(3)成立：

Δy(k+1)=φT(k)·Δu(k)

(3)

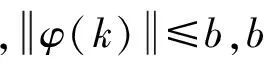
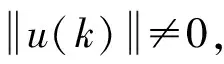
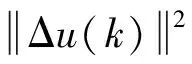
(4)

式中，y*(k+1)是系统的期望输出;λ是惩罚系数，即限制Δu(k)的变化速度。

由于式(3)可以表示为式(5):

y(k+1)=y(k)+φT(k)·Δu(k)

(5)

为了在该代价函数下，获得最优的输入控制变量，将式5代入式4，并计算∂J(u(k))/∂u(k)=0则得:

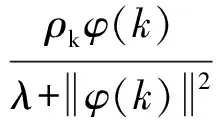
(6)

式中，λ是权重系数;ρ是步长系数;φ(k)可由式(7)计算

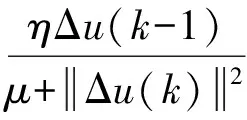
(7)

式中，μ是权重系数;η是步长系数。从式(6)看出，输入变量u(k)的计算仅和系统的输入输出变量有关，没有任何数学模型和规则可供参考。由于任何系统的输入输出信息包含着系统的所有特性，故无模型自适应控制系统充分系统的输入输出信息，尤其是系统的输出信息，因为输出信息包含着系统的滞后时间信息，这个信息对于系统的参数选择起着至关重要的作用，同时有效的利用系统的输入信息，根据系统的输入输出信息，寻找一种简单的、有效的控制策略计算控制系统的输入变量，使系统的输出满足我们的要求。本设计中借用PWM控制的思想，在温度上升的中后期，采用每加热一个工频周期，停止加热几个工频周期的方法，从而有效地克服了采样间隔时间过长而导致加热时间或者冷却时间过长而引起温度波动较大的问题。

5 仿真研究及结果分析

本文分别对不同的初始温度，不同的设定温度，不同的采样点数L分别进行了仿真，其中μ=1，η=0.1，λ=0.01，仿真结果如图2～5所示。

从上面的温度控制仿真输出波形可以看出，不同的L值，对控制系统的输出性能的影响是不同的。如果L数值大，上升时间变大，没有任何超调产生，输出波形如图2、4所示；如果L数值小，系统输出具有超调，系统输出波形如图3、5所示。由于L是φ(k)的采样点数，L数值大，计算量大，L数值小，计算量小，L的数值必须和系统相配合。当温度控制系统的设定输入信号发生变化时，此时温度系统的增益也产生了变化，如果L数值不变，控制效果也不好，这种情况从图3、5中可以看出，这主要是由于系统的参数发生了变化所引起的。

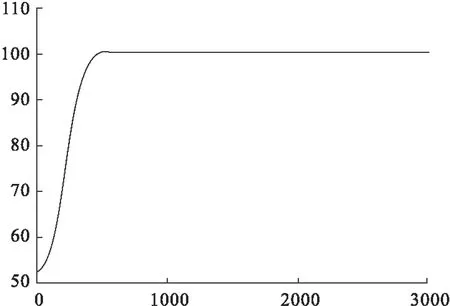
图2 温度设定100℃，L=90

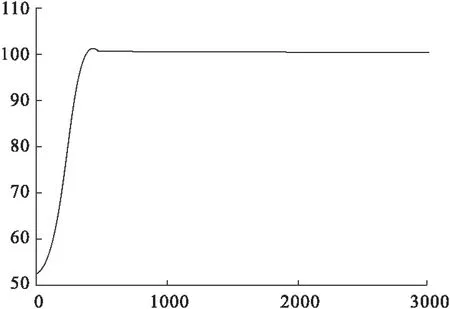
图3 温度设定100℃，L=70

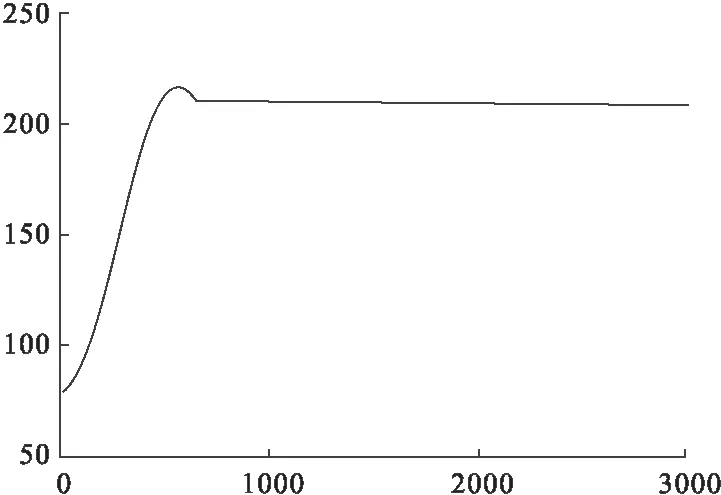
图4 温度设定200℃，L=90

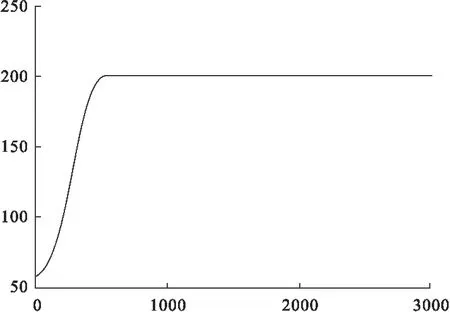
图5 温度设定200℃，L=70

6 结论

本文通过无模型自适应控制在温度控制系统中的应用研究，分析了系统在不同的初始温度，不同的设定温度，不同的采样点数下的仿真结果，对比了多种温度输出轨迹曲线。讨论了的采样点数对温度控制系统性能指标的影响，指出了采样点数的选取原则；解释了温度控制系统的特点和难以控制的根本原因，是系统的反馈信号严重滞后于系统的输入信号，这样从反馈通道得到的反馈信息并不是当前的输入产生的，是之前某一时刻输入信号作用而产生的。

根据温度控制系统的滞后特点，把无模型自适应控制的控制思想应用到温度控制系统的设计中，设计了基于无模型自适应控制的控制器，该控制器充分利用温度的控制信号和实际的温度输出检测数值，借助于径向基函数的神经网络评估系统，在线计算新的控制信号数值。从仿真输出数据看出，该系统的动态响应快，跟踪性能好，抗干扰能力强，证明了该方法的有效性。

[1] 刘金琨,先进PID控制MATLAB仿真[M],电子工业出版社,2004.

[2] 侯忠生.无模型自适应控制的现状与展望[J].控制理论与应用.2006,23(4):586-592.

[3] 吴宏鑫.全系数自适应控制理论及其应用[M].国防工业出版社,1990.

[4] 韩志刚,汪国强.无模型控制率串级形式及其应用[J].自动化学报，2006,32(3):345-352.

[5] 周黎英,赵国树.模糊PID控制算法在恒速升温系统中的应用[J].仪器仪表学报,2008,29(2):405-409.

[6] Leandro dos Santos Coelho,Marcelo Wicthoff Pessoa,etc.Model-free adaptive control design using evolutionary-neural compensator.Expert Systems with Applications.2009.05.042.

[7] Leandro dos Santos Coelho,Antonio Augusto Rodrigues Coelho.Model-free adaptive control optimization using a chaotic particle swarm approach[J].Chaos,Solitons & Fractals,2008,8(4):1-9.

[8] 曹荣敏,侯忠生.永磁直线电机的无模型学习自适应控制[J].电气传动，2006，36(7):22-25.

[9] 曹荣敏,侯忠生.永磁直线电机的无模型自适应控制方法研究[J].计算机工程与设计，2007,3:1433-1436.

DesignofTemperatureControlSystemBasedonMFAC

CHENMing

(School of Physics and Electronic Engineering,Hubei University of Arts and Science,Xiangyang, 441053,China)

The dynamic process of temperature control system and nature of MFAC(model free adaptive controller) were analyzed.The feature of nonlinear,hysteresis and time-varying were analyzed.PWM control thought was adopted at the process of heating and cooling.This method decreased the temperature ripple introduced by long heating and cooling period.The results show that the MFAC can shorten the rising time of the temperature control system,improve the immune of disturbance and reduce the temperature ripple.

modelfree adaptive control;temperature control;traditional PID controller

1004-289X(2013)06-0040-04

TP273+.2

B

2013-09-03