异步电机矢量控制系统仿真实现

，，

(邵阳学院 电气工程系，湖南 邵阳 422000)

异步电机矢量控制系统仿真实现

尹进田，刘丽，石赛美

(邵阳学院 电气工程系，湖南 邵阳 422000)

从异步电机在同步旋转坐标系上( M 、T 坐标系)的数学模型入手，构造出异步电机矢量控制系统模型，并应用Matlab/Simulink对其进行仿真，验证了系统模型的正确性。由于在使用中只需输入不同电机的参数即可，因而大大提高了仿真效率和可靠性，具有直观、灵活、精度高等优点。

异步电机；矢量控制；数学模型；仿真

1 引言

异步电机作为交流传动系统中一个主要执行环节，其本身是一个高阶次、非线形、强耦合的多变量系统，其动、静态性能相当复杂。在进行复杂的系统设计时，采用计算机仿真的方法是十分有效和必要的。

Matlab是一种交互式仿真系统，特别适用于动态系统的建模和仿真。本文结合Matlab/Simulink的特点，应用Simulink模块库及在Simulink环境下的电力系统仿真模块库(Power System Blockset),构造一种异步电机矢量控制系统的数学模型及仿真方法。通过可靠的仿真实验，说明该模型的正确性，为同类系统提供了一种有效、可靠的研究依据[1]。

2 基于M 、T坐标的异步电机数学模型

2.1基本思想

对于电机的数学模型的研究，下列假设条件是被广泛认可的：①忽略磁路饱和及铁耗，认为各绕组的自感、互感都是线性的；②三相绕组对称，磁势沿气隙周围按正弦分布；③不考虑温度和频率变化对电机的影响。但是，即使在上述假设条件下，要分析和求解异步电机在ABC坐标系上的数学模型依然是十分困难的。

1971年，联邦德国的F.Blaschke 等人首先提出在普通的三相交流电动机上设法模拟直流电动机控制转矩的规律，即矢量变换控制，这种方法很好地解决了异步电机的许多问题。其基本思想是把三相交流电动机模型在下列两条原则：①变换前后功率不变；②变换前后合成磁动势不变下等效地变换成类似的直流电动机模型。这样就可以模拟直流电动机去控制交流电动机，如图1所示，其中3/2变换为三相/二相变换，VR变换为矢量旋转变换。

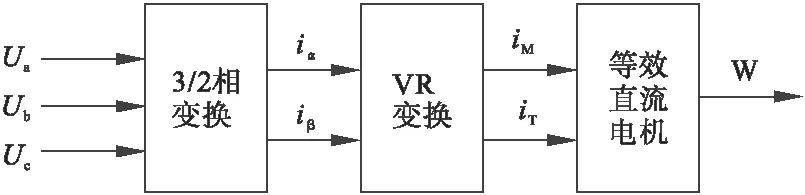
图1 基于M 、T坐标系的异步电机框图

(1)3/2变换—通过数学上的磁动势坐标变换方法，把三相交流电流与二相交流电流做等效变换，即三相静止坐标U、V、W到二相静止坐标α、β之间的变换，变换后的式子为：

(1)

(2)矢量旋转变换——所谓矢量旋转变换就是交流二相α、β绕组和直流二相M 、T绕组之间电流的变换，是静止直角坐标系与旋转直角坐标系之间的转换，简称VR变换，变换后的式子为：

(2)

这里的φ为α轴与M轴的夹角，它随着时间的变化而变化。此时，转子总磁链Ψ2矢量的方向为M轴，逆时针90°与Ψ2垂直的方向为T轴。当观察者站在铁芯上和绕组一起旋转时，在他看来，M、T绕组是两个通以直流电的相互垂直的固定绕组，这就与等效的直流电动机绕组没有差别了。则M绕组相当于励磁绕组，T绕组为电枢绕组[2,3]。

2.2数学模型

根据以上理论，给出异步电机两相以同步速旋转,按转子磁场定向的M、T坐标的数学模型。

(1)电压方程

(3)

(2)磁链方程

由于M轴与转子总磁链Ψ2重合，T轴与矢量Ψ2垂直，所以有ψM2=ψ2,ψT2=0

(4)

把(4)式中的第三、四式写成电流形式为：

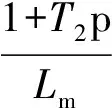
(5)

此处T2=Lr/R2为转子时间常数。

(3)电压矩阵方程

由于转子短路，则有UM2=UT2=0

(6)

(4)电磁转矩方程

Te=npLm(iT1iM2-iM1iT2)

将(5)式代入(6)式，得到

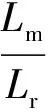
(7)

其中：UM1、UT1、UM2、UT2为电机M、T轴定、转子电压；iM1、iT1、iM2、iT2为电机M、T 轴定、转子电流；ΨM1、ΨT1、ΨM2、ΨT2为电机M、T轴定、转子磁链；R1、R2为定转子电阻；L1、L2为定转子自感；Lm为定转子互感；ω1为同步角速度；ω2为转差角频率；p为微分算子；np为极数。

式(5)表明转子磁链Ψ2仅由iM1产生，而与iT1无关，所以我们称iM1为定子电流的励磁分量，Ψ2的稳态值由iM1决定；式(7)表明，当iM1不变，即Ψ2不变时，iT1变化，转矩Te立刻随之正比地变化，没有滞后，可以认为iT1是定子电流的转矩分量。

总之，由于M、T坐标按转子磁场定向，在定子电流的两个分量之间实现了解耦。iM1只影响Ψ2，iT1只影响Te，这就与直流电机的励磁电流和电枢电流相对应，这样就大大简化了多变量、强耦合的异步电机的控制问题。

由(4)式中的第四行可得出T轴上定子电流iT1和转子电流iT2的动态关系为：

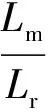
(8)

由(6)式中的第四行可得：

0=w2(LmiM1+LriM2)+R2iT2=w2ψ2+R2iT2

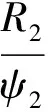
(9)

把(8)代入(9)考虑T2=Lr/R2，则可求得转差w2与T轴上定子电流iT1的关系为：

(10)

转差频率控制可由此式来实现。

3 Matlab/Simulink 仿真异步电机数学模型

3.1异步电机矢量控制系统框图

如图2所示为一个磁链开环而转速、电流闭环的交/交变频异步电机矢量控制系统原理图，该系统主要由异步电机矢量变换模型、定子给定电流iM1*和iT1*计算、磁链位置角θ计算、速度检测等模块组成[4]。

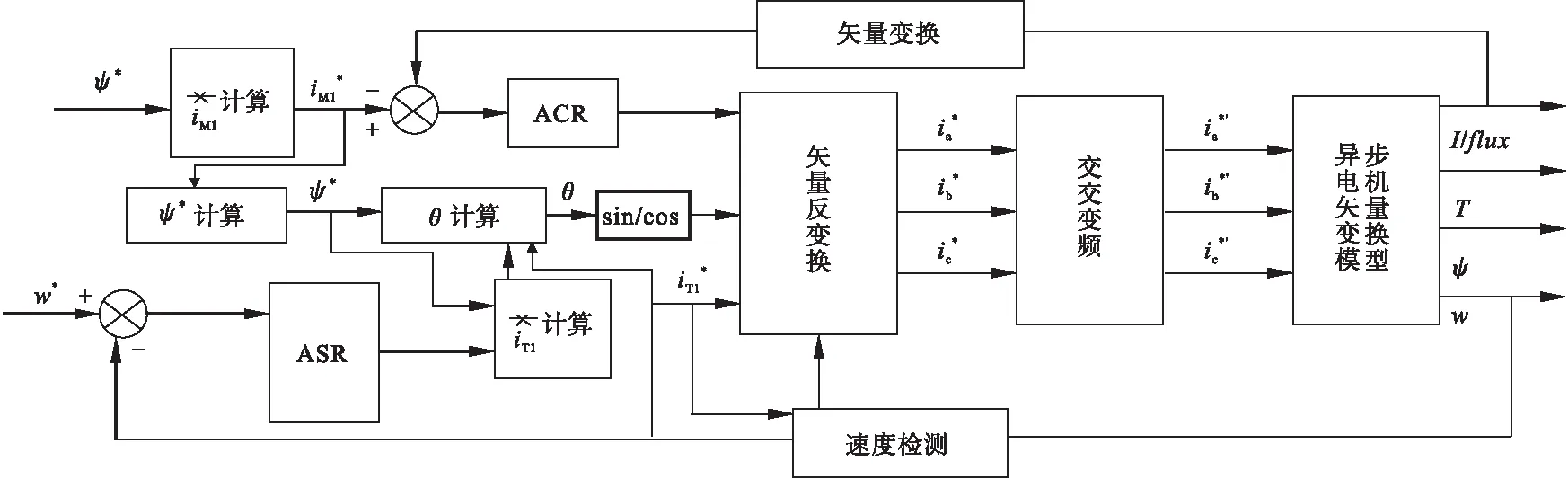
图2 交/交变频异步电机矢量控制系统原理图

2.1.1 定子电流控制系统

在该系统中，磁链ψ*为固定值，经“iM1*计算电路”得到定子电流的励磁分量给定值iM1*，定子电流的转矩分量给定iT1*来自转速调节器(ASR)和“iT1*计算电路”的输出，有了iM1*后，经矢量变换(即VR-1和2/3变换)，供给交/交变频器及异步电机。

为了使得定子三相电流的实际值等于给定值，系统中设计了以ACR为核心的电流控制系统。该电流控制系统的输入来自定子三相电流的实际值iM1、iT1，其输出作用于交/交变频器，将其改造成具有电流源特性的变频器。这样，其电流反馈I/flux就能随时对三相电流的实际值进行修正，达到电流闭环的目的。

3.1.2 磁链位置角θ计算

3.1.3 速度闭环控制系统

异步电机矢量控制重点控制的变量就是电机的速度，在高性能调速中速度均采用速度闭环控制。

(1)速度调节器(ASR)

本系统中的速度调节器是一个比例-积分(PI)调节器，其输入是给定速度值ω*与实际速度值ω的偏差，输出为定子电流的转矩分量给定值iT1*。

(2)速度检测环节

为了得到高性能的调速系统，转速闭环控制是必要的，速度检测环节成为关键的一环。常用的速度检测方法有：用测速发电机测量转速、用光电方法测速、用轴编码测速等。这些利用速度传感器的方法不可避免地要在电机上安装硬件装置，这对于笼式异步电机而言，速度传感器的安装将其坚固、简单、低成本的优点。所以在本系统中，我们采用无速度传感器技术，其中一种比较简单的方法就是基于转矩电流误差推算速度的方法，即认为异步电机的电磁转矩仅由转矩电流分量iT1产生。因此我们构造如下算式为异步电机速度推算机构：

(11)

3.2异步电机矢量控制系统的Simulink仿真模型

如图3包含了异步电机矢量变换封装模型、iM1*计算封装模型、iT1*计算封装模型、ψ*计算封装模型、θ计算封装模型模块、速度检测估计模型共6个模型[5]。这些模块由Simulink调用库模块和Simulink/Power System模块建立，然后封装成Subsystem。

4 仿真实例

在设计中选用仿真电机参数为：np=2，Tenom=8.84N*m，Inom=2.6A，R1=4.25Ω，R2= 3.24Ω，Lm=0.671H，Lr=0.671H，Ls= 0.651H，J=0.02N*m2。以上参数均可以写入M文件，这样在仿真前，只需要运行该M文件，就可以向Simulink提供仿真时所需参数，同时也方便参数的修改。

按图3设计，给异步电机直接加入380V，50Hz的额定电压，转速输入为一阶跃函数，初值为250 rad/s,磁通设为一定值1.1Wb。

电动机由空载运行，在t=0.3s 时突加负载

T=3.5N*m，获得仿真曲线如图4～7，由输出波形可以看出，所建立的模型符合电机的运行特性。

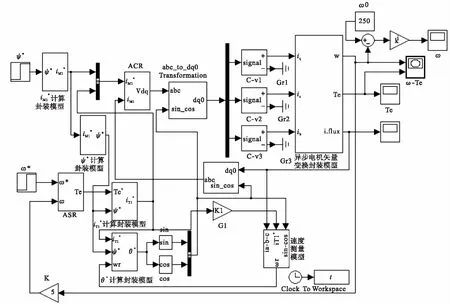
图3 异步电机矢量控制系统的Simulink仿真模型

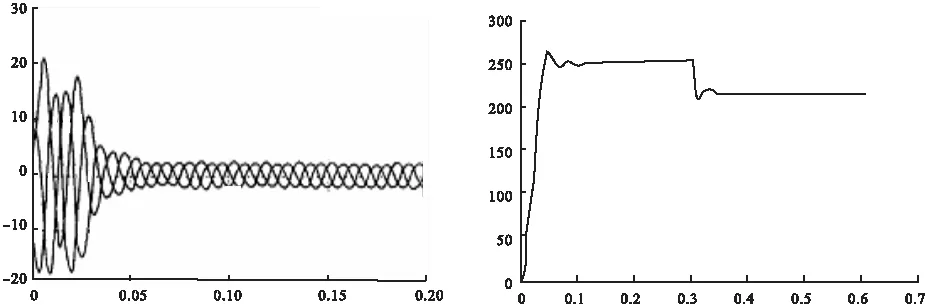
图4 电机三相电流波形 图5 电机转速ω波形

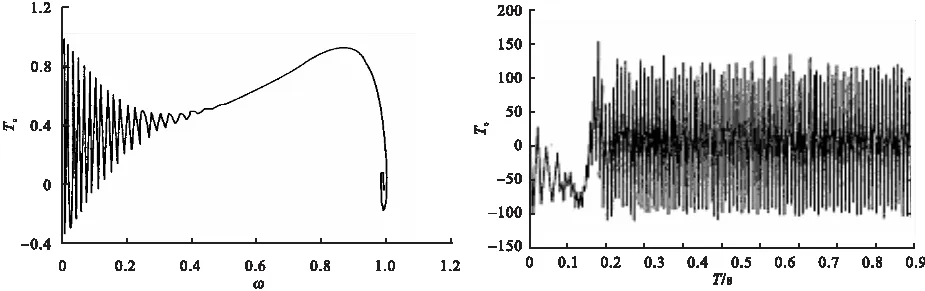
图6 电机Te-ω波形 图7 电机转矩Te 波形

5 结果分析与结论

通过仿真试验获得的仿真曲线,充分验证了在异步电机矢量变换数学模型的基础上建立仿真模型的正确性。采用Simulink进行异步电机调速系统仿真,无需编程、直观、灵活,对于开发和研究调速系统有着重要的意义。

[1] 杨洋.基于Matlab/ Simulink的异步电机矢量控制调速系统仿真[J].湖南大学学报,2000,27(2):50-55.

[2] 周渊深.异步电机交/交变频调速系统的建模与仿真[J].微特电机,2002,30(5):10-12.

[3] 陈立杨,周文卫.异步电机SVPWM矢量控制系统仿真与实现[J].电气传动自动化，2011(6):19-23.

[4] 张春喜,廖文建,等.异步电机SVPWM矢量控制仿真分析[J].电机与控制学报,2008(2):46-50.

[5] 朝泽云,康勇,等.异步电机矢量控制系统的建模与仿真[J].电机与控制应用,2007(3):15-21.

2013-01-15

尹丽田(1981-)男，硕士，讲师，主要研究方向电气自动化；

刘丽(1984-)女，硕士，讲师，主要研究方向：测控自动化。

SimulationandRealizationofVectorControlSystemofAsynchronousMotors

YINJin-tian,LIULi,SHISai-mei

(Department of Electrical Engineering,Hunan University of Shaoyang,Shaoyang 422000,China)

The paper introduces a dynamic simulation model of vector-control asynchronous motor according to its mathematics model in the rotational coordinates system(M 、T system),then simulate it with Matlab/Simulink,and it shows the validity of the model.The model can be conveniently used by putting proper motor parameters,so it can greatly raise simulation efficiency and has audio-visual、convenient、flexibility.

asynchronous motor ;vector control;mathematics model;simulation

1004-289X(2013)06-0015-04

TM343

B

湖南省教育厅项目编号：11C1131