高超声速飞行器末段轨迹快速优化

杨良, 周浩, 陈万春

(北京航空航天大学 宇航学院, 北京 100191)

高超声速飞行器末段轨迹快速优化

杨良, 周浩, 陈万春

(北京航空航天大学 宇航学院, 北京 100191)

利用高斯伪谱法求解具有路径约束和落角、落速等终端约束条件下的高超声速飞行器末段轨迹优化问题。分析了不同LG节点数目对该问题求解精度和计算时间的影响,以及不同LG节点的拟合多项式与实际积分结果之间的相对误差关系。根据精度需要,选择合适的LG节点进行优化,分析了状态变量与积分结果的相对误差传播情况。仿真结果表明,采用节点分析后的高斯伪谱法在求解该问题上具有较高的计算精度和计算效率。

高超声速飞行器; 轨迹优化; 高斯伪谱法

0 引言

高超声速飞行器对控制变量比较敏感,并且需要考虑最大动压约束和最大过载约束等情况,因此,可行解就在一个非常狭窄的范围内,许多学者对这一问题进行了研究。近十几年来,随着伪谱法在优化领域的应用,能够较快地寻到最优解[1]。文献[2]使用间接法对高超声速飞行器的滑行轨迹进行了优化。文献[3-4]分别利用高斯伪谱法对高超声速飞行器的再入轨迹进行了优化,文献[4]同时提出了分段串行优化策略。文献[5]利用Legendre伪谱法对高超声速飞行器的再入轨迹进行了优化,同时利用Hamilton函数分析了解的最优性。文献[6]利用高斯伪谱法对路径点与禁飞区等多过程约束的高超声速飞行器进行了轨迹优化。这些研究都集中在高超声速飞行器的滑翔段,很少有研究对不同LG节点与求解精度进行定量的分析。本文针对高超声速飞行器末段轨迹优化这一特定问题进行研究,分析了不同节点对计算时间和计算精度的影响,利用Hamilton函数分析了求解结果的最优性,计算得到不同LG节点的拟合多项式与实际积分结果之间的相对误差关系。通过相对误差的关系,根据精度要求,选择合适的LG节点,仿真结果表明,选取合适LG节点的高斯伪谱法[7]在求解该问题上具有较高的计算精度和计算效率,最后分析了不同状态变量之间的误差传播关系。对于高超声速飞行器的末段轨迹优化问题,准确的选点能够保证较高的计算精度和计算效率,这为高斯伪谱法的在线制导提供了较好的仿真数据。

1 高斯伪谱法介绍

考虑下面的最优控制问题,状态量x(τ)∈Rn,控制量u(τ)∈Rm,初始时刻和终端时刻为t0和tf。

J[u,x,τf]=Φ[x(τ0),x(τf),τ0,τf]+

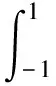
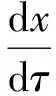
φ[x(-1),x(1),t0,tf]=0∈Rq

C[x(-1),x(1),t0,tf]≤0∈Rc

式中,φ为过程等式约束;C为过程不等式约束。一般的最优控制问题可以通过下面的公式转化为时间区域为τ∈[-1,1]的问题。

t=(tf-t0)τ/2+(tf-t0)/2

高斯伪谱法与文献[8-9]中介绍的Legendre伪谱法和Chebyshev伪谱法一样,都是采用插值多项式来逼近状态变量和控制变量。

在LG节点的每个Lagrange多项式的微分方程可以用一个微分矩阵来逼近,这个矩阵就是D∈RN×N+1,微分矩阵的元素可以表示为:

式中,k=1,…,N;i=0,…,N。这样状态微分方程就可以通过微分矩阵转换为代数约束,可表示为:

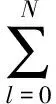
式中,ωk为高斯权函数。连续的性能指标函数也可以通过积分公式表示为:

J=Φ[x(-1),x(1),t0,tf]+

φ(X0,Xf,t0,tf)=0,C(Xk,Uk,τk;t0,tf)≤0

不规范处方主要包括：①处方超量，如普通处方超过7天量，急诊处方超过3天量，省特约处方超过7天量，无特殊治疗需要处方超过1个月用量等；②临床诊断书写不全、病人信息不全；③医生输入错误；④医师处方未签名（盖章）或与留样不一致；⑤处方上药品品种数量超过规定（5种）；⑥处方修改未签名盖章，也未注明修改日期；⑦处方用笺不规范，如门诊手写处方用的是住院处方或自费药房处方。

这样就把连续的Bolza问题转换为非线性规划(NLP)问题,通过成熟的非线性规划求解器就可以找到该问题的最优解。

2 高超声速飞行器动力学模型

2.1 动力学方程

大气相对于地球静止的无动力三自由度质点弹道运动学方程[10]为:

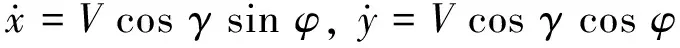
式中,x,y,z为大地坐标;V为地球相对速度;γ为航迹角;φ为航向角;α为迎角;σ为侧倾角;g=μ/r2为重力加速度;μ为地球重力加速度常数。升力L和阻力D如下:

L=qSrefCL/m,D=qSrefCD/m

式中,q=ρV2/2为飞行过程中的动压;CL为升力系数;CD为阻力系数;Sref为飞行器的参考面积;m为飞行器质量;ρ为大气密度,ρ=ρ0exp(-βH),其中ρ0为海平面大气密度,H=r-Re为高度,Re为地球半径,β为密度常数。

2.2 约束条件

从结构和热防护的角度出发,要求高超声速飞行器在飞行过程中满足动压约束以及过载约束,其约束的表达式为:

q=(1/2)ρV2≤qmax,nz=L/(mg)≤nzmax

式中,qmax,nzmax根据具体飞行器的设计进行选取。

|u1|≤u1max, |u2|≤u2max

2.3 优化性能指标

为了保证优化得到的控制变量能够足够光滑,选取各个控制变量的平方和最小这一性能指标作为优化性能指标。各个控制变量的平方和最小也意味着飞行器在飞行过程中以消耗能量最小的方式达到所满足的条件,其具体表达形式为:

3 数值计算与分析

3.1LG节点数目的影响

选取高斯伪谱法的LG节点数为60,30,15,10,6分别对该问题进行优化。所有计算均在Window 7的系统环境下运行MATLAB 2008B进行计算,非线性规划问题采用著名的snopt软件包进行求解。

采用不同LG节点进行优化的仿真结果如图1所示。由图可知,这些结果非常相似,多次优化的结果都同时收敛到最优解。从各状态变量的曲线来看,其最优结果都非常光滑。

通过对不同拟合多项式的相对节点误差比较,采用阶数相对较少的多项式直接逼近各状态变量就可以达到较高的逼近精度,这也意味着能够选取很少的LG节点达到较高的计算精度。LG节点的减少同时也能够带来通过高斯伪谱法离散后的非线性规划问题的规模减少。但随着节点数目的减少,计算精度也会下降,从图中可以看出,采用6个LG节点的优化结果明显出现较大的偏差。

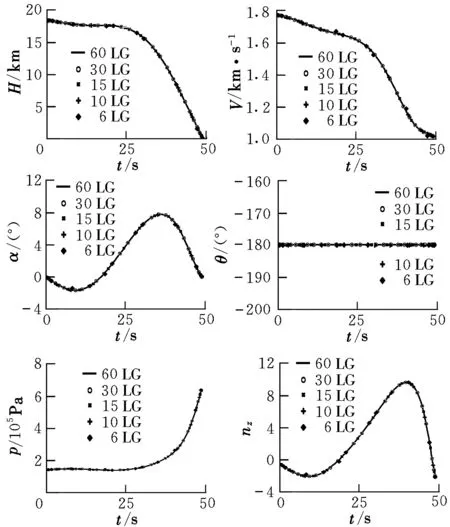
图1 优化结果仿真曲线Fig.1 Curve of optimization simulation

表1分别对不同LG节点数进行优化的计算时间进行对比。随着节点的减少,优化变量和计算时间大大减少,优化问题的规模得到了很大的改善。从表中可以看出,采用10个LG节点的计算时间相对于60个LG节点也从520.71 s减少到4.975 1 s。

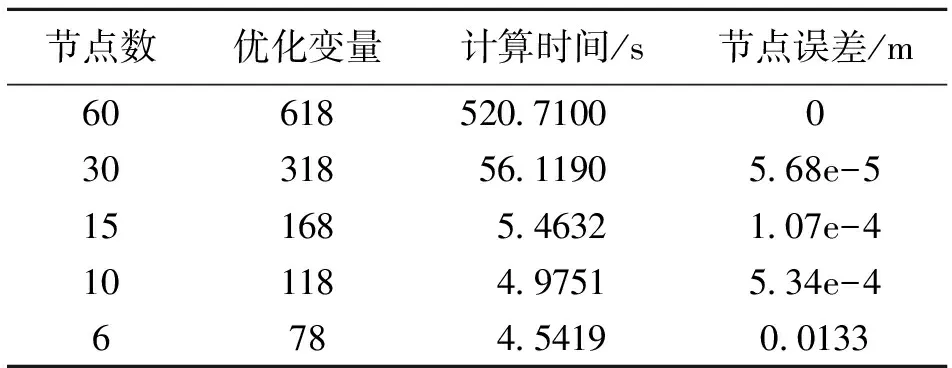
表1 不同LG节点的优化结果Table 1 Optimization of various LG nodes

3.2 最优性验证

根据文献[7],可以通过约束的Lagrange乘子估算出最优控制问题的协态变量。这样就提供了一种对所得结果进行最优性验证的方法。

根据最优控制理论,在约束不受限的情况下,Hamilton方程恒等于零;在受限情况下,其Hamilton函数应该尽可能地接近于不受限的Hamilton函数,这样就为解的最优性提供了一个验证(见图2)。在Hamilton函数曲线上,Hamilton函数的数值结果基本接近于零,通过Hamilton函数的近似性,保证了解的最优性。

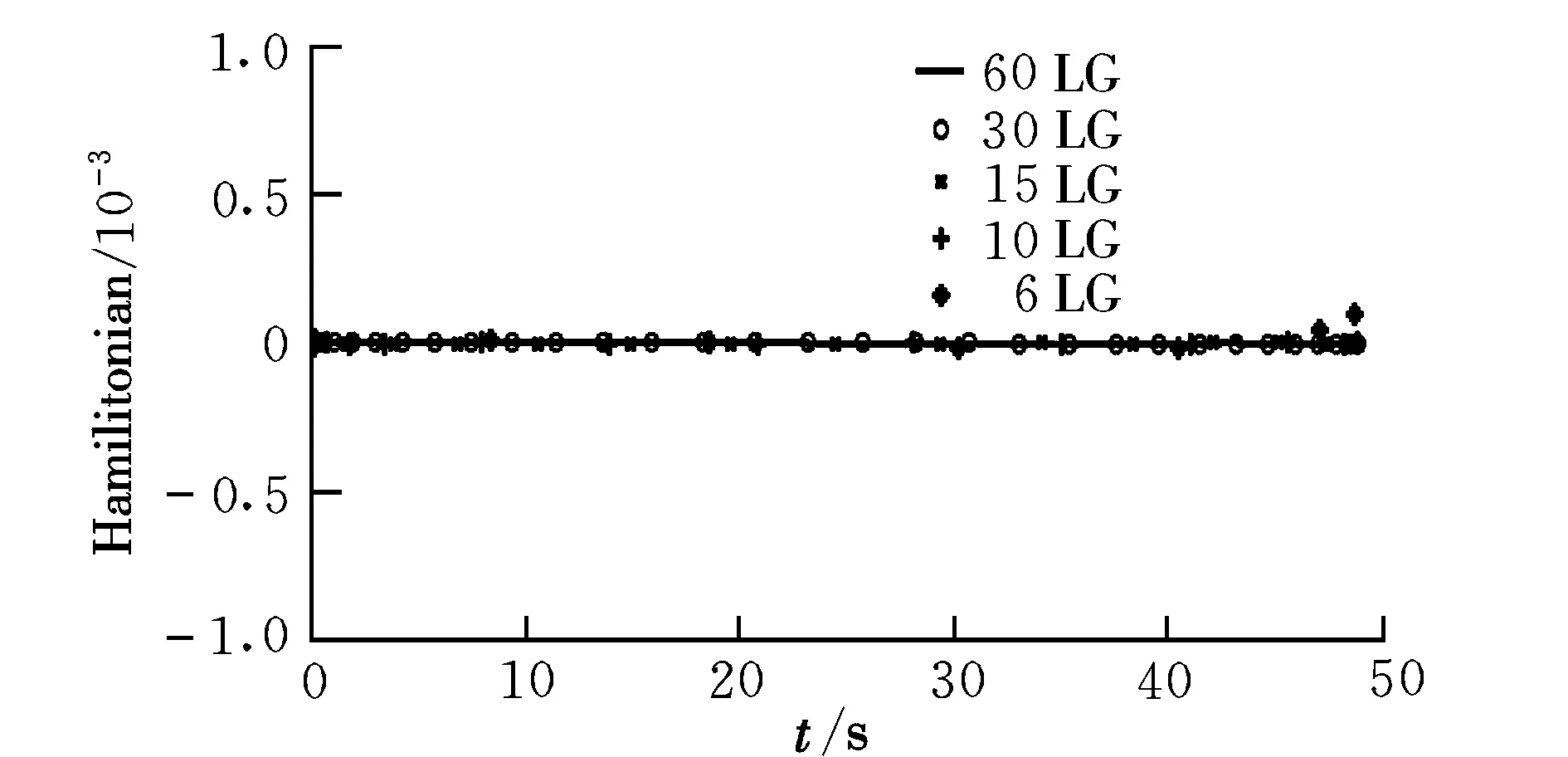
图2 Hamilton函数Fig.2 Hamilton function

3.3 优化结果比较与误差分析

图3为不同LG节点与积分弹道的相对误差之间的关系。从图中可以看出,随着LG节点的增加,误差精度越来越小,但变化趋势趋于平缓,在较少的LG节点时,精度出现比较大的变化,因此,根据精度要求,合理选择LG节点个数非常重要。图4为采用10个LG节点的高斯伪谱法优化弹道与积分弹道进行对比的结果,通过MATLAB 2008B中的Simulink搭建动力学模型实现弹道积分,积分方法选用四阶R-K法。从图中可以看出,优化结果与积分结果基本相同。

图3 相对误差精度与LG节点的关系Fig.3 Relationship between relative error and LG nodes

图4 优化结果对比曲线Fig.4 Comparison of optimization results

图5为各个状态变量的相对误差传播变化情况,是通过各个状态变量的积分结果与优化结果的Lagrange插值多项式相减,然后除以相对系数。从图中可以看出,各个状态量之间的相对误差都很小,且呈振荡分布,在LG节点上达到优化算法的可行性精度。x和y方向的相对误差基本上保持在10-5数量级上,而z方向、速度和航迹角的相对误差基本保持在10-4数量级上,最小的为航向角相对误差,保持在10-8数量级上。因此,采用10个LG节点的高斯伪谱法在处理高超声速飞行器末段轨迹快速优化问题上,能够很快地收敛到全局最优解,并且具有很高的计算效率与计算精度。

图5 误差的仿真结果Fig.5 Results of error simulation

4 结束语

本文针对高超声速飞行器的末段轨迹快速优化问题进行了研究,采用高斯伪谱法进行优化。分析了不同LG节点对计算时间和计算效率的影响,不同LG节点的拟合多项式与实际积分结果之间的相对误差关系以及状态的误差传播情况。结果表明,合理选择LG节点的高斯伪谱法具有很高的计算精度和计算效率。高精度、高效率的优化结果也为高超声速飞行器的末段轨迹在线优化实现提供了很好的计算依据,下一步将以本文工作为基础,重点研究高斯伪谱法的在线优化问题。

[1] Betts J T.Survey of numerical methods for trajectory optimization[J].Journal of Guidance,Control,and Dynamics,1998,21(2):193-207.

[2] 周浩,陈万春,殷兴良.高超声速飞行器滑行轨迹优化[J].北京航空航天大学学报,2006,32(5):513-517.

[3] 周文雅,杨涤,李顺利.利用高斯伪谱法求解升力航天器最优再入轨迹[J].南京理工大学学报(自然科学版),2010,34(1):85-90.

[4] 雍恩米,唐国金,陈磊.基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J].宇航学报,2008,29(6):1765-1772.

[5] Rao A V,Clarke K A.Performance optimization of a maneuvering re-entering vehicle suing a legendre pseudospectral method [R].AIAA-2002-4885,2002.

[6] Jorris T R,Rao A V.Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J].Journal of Guidance,Control,and Dynamics,2009,32(2):551-572.

[7] Benson D A,Huntington G T. Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1435-1440.

[8] Fahroo F,Ross I M.Costate estimation by a Legendre pseudospectral method[J].Journal of Guidance,Control,and Dynamics,2001,24(2):270-277.

[9] Fahroo F,Ross I M.Direct trajectory optimization by a Chebyshev pseudospectral method [J].Journal of Guidance,Control,and Dynamics,2002,25(1):160-166.

[10] Vinh N X.Flight mechanics of high-performance aircraft[M].Cambridge,England:Cambridge University Press,1993:22-25.

Fastterminaltrajectoryoptimizationforhypersonicspacecraft

YANG Liang, ZHOU Hao, CHEN Wan-chun

(School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing 100191, China)

In this paper, the terminal trajectory optimization with the constraints on process, impact angles and impact speed for hypersonic spacecraft is solved by Gauss pesudospctral method. By various Lambert-Gauss nodes operated to optimize this problem, the effect of the number of nodes on calculation time and calculation efficiency is studied. By comparing optimal results of various nodes with integral results, the relative error is obtained. According to specified accuracy, appropriate LG node is selected to optimize this problem and the extensive analysis of propagation relationship of the relative errors between Lagrange interpolation polynomial and integrated states is carried out. The results show that Gauss pseudospectral method applying nodes analysis is of high calculation accuracy and high calculation time to solve this problem.

hypersonic spacecraft; trajectory optimization; Gauss pseudospectral method

V412.4

A

1002-0853(2013)04-0341-04

2012-11-14;

2013-03-24; < class="emphasis_bold">网络出版时间

时间:2013-06-06 12:25

杨良(1985-)，男，湖南常德人，博士研究生，研究方向为飞行动力学及弹道优化。

(编辑：方春玲)