基于子空间和PEM的无人直升机两阶段参数辨识

邵明强, 李广文, 徐恒

(西北工业大学 自动化学院, 陕西 西安 710072)

基于子空间和PEM的无人直升机两阶段参数辨识

邵明强, 李广文, 徐恒

(西北工业大学 自动化学院, 陕西 西安 710072)

在研究子空间辨识方法和预测误差方法(PEM)的基础上,提出了一种两阶段辨识方法,研究无人直升机的参数辨识问题。首先采用子空间方法得到初始参数模型,然后通过PEM方法得到参数化的直升机模型。为验证方法的有效性,以某型无人直升机实测数据为例进行参数辨识,结果表明该方法有良好的辨识精度。

无人直升机; 子空间; 预测误差法; 参数辨识

0 引言

无人直升机是一个非常复杂的控制对象,具有多输入多输出、高度非线性、开环不稳定、复杂的动力学特性和轴间耦合强等特点[1-2],使得准确建立无人直升机的飞行力学模型非常困难。无人直升机的飞行力学建模方法主要有机理建模方法和系统辨识建模方法[3]。前者得到的模型参数精度往往不高,而且通常需要采用实验的方法弥补气动力计算的不足,会花费大量的人力、物力及财力。系统辨识建模方法是利用直升机输入-输出数据的外部特性去寻找一个具有等价输入-输出特性的模型。与传统机理建模方法相比,采用系统辨识方法建立的飞行力学模型在环境条件变化情况下更具有适用性,并且能在较宽的区间内保持良好的准确性[3],且经济效益好,这些优势使系统辨识在无人直升机飞行力学建模中得到了广泛应用。

近年来国内外研究者利用系统辨识方法对微小型无人直升机进行建模,也取得了很大进展。美国采用基于频域响应的频域方法开发出一套对旋翼飞行器辨识的软件CIFER,并成功辨识了包括CH-47,BO-105,UH-60等直升机的飞行力学模型。目前,这些辨识结果已经被用于飞行控制律综合设计与优化软件CONDULT当中[4]。国内北京航空航天大学、南京航空航天大学等多所高校也在该领域展开了研究[5-7];但是频域辨识方法通常需要带宽很大的通道输入[5],而在扫频试验中低频激励很难实现,高频激励又很容易超过无人直升机的正常工作范围。小型无人直升机往往采用时域辨识方法,利用遥控飞行时采集的数据辨识无人直升机模型。在时域辨识方法中常用的算法有预测误差法(PEM)和子空间方法。

PEM算法是一种精确度较高的辨识算法,不要求辨识数据的概率分布式[6],因此适用范围比较广。但PEM算法受初始状态影响很大,初始状态不理想时辨识精度较低,同时算法较复杂、效率不高。

子空间辨识算法是20世纪90年代初出现的一种针对线性时不变、多输入-多输出系统的状态空间模型辨识方法,综合了系统理论、线性代数和统计学三方面的思想,能够直接通过输入-输出数据估计多变量系统的状态空间模型[3],适用于多变量系统辨识[8]。但是由于子空间算法不是按照某个最优准则求解得到的,所以仍然是“次优的”。对于任意可观可控的线性系统,子空间方法唯一的假设为噪声与系统的输入无关,这在实际系统中是很难满足的,因此子空间算法得到的辨识结果精度较低。

本文采用一种两阶段辨识算法进行无人直升机的参数辨识。利用子空间算法得到一个次优的初始模型,作为PEM算法的初始模型进行更高精度的辨识。

1 小型无人直升机参数化模型的建立

直升机的飞行力学方程描述了直升机的运动特性,它取决于直升机的空气动力特性、几何特性以及惯性特性。但是小型无人直升机各部分的空气动力学特性和操纵参数的相互关系非常复杂,同时机身与旋翼之间存在强烈的耦合,想要直接辨识出非线性模型参数非常困难,因此现有的算法大都是针对线性系统的。实际中,由于小型无人直升机很少进行大机动飞行,线性化模型能够较好地描述在大多数情况下的飞行特性,便于进行控制系统设计,因此线性化模型辨识是很有意义的。

本文根据直升机运动学方程,在直升机巡航状态下根据小扰动和小角度假设进行线性化,在配平状态附近可以得到小型无人直升机的六自由度线性刚体模型[9-11]:

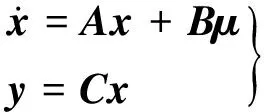
(1)

其中:

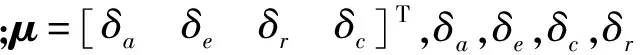
2 辨识算法

子空间辨识算法辨识系统模型高效、方便,因其辨识过程均为矩阵运算,不需要反复循环迭代,运算速度很快。但正是因为子空间辨识方法仅通过矩阵的投影计算、SVD分解和QR分解来计算系统的数学模型,故其解只是一个“次优解”,其精度与传统辨识算法相比较差。另外对于任意可控、可观系统,子空间辨识方法最重要的前提是假设噪声与系统的输入无关。但在实际飞行试验中,当对某一通道进行激励的同时,需要控制其它通道以保证直升机能够平稳飞行,造成直升机处于部分闭环飞行,噪声和输入不是完全无关,导致辨识结果是有偏的。虽然该结果有偏,却非常接近最优解。寻优算法几乎不可避免地面临着寻优过程中可能出现的局部最优现象。影响算法在寻优过程中出现局部最优现象的主要因素有两方面:一方面在于寻优方法的全局寻优能力;另一方面在于寻优的初值。当初始寻优参数接近全局最优时,通常可以快速准确的得到全局最优值[3]。因此可以由子空间方法快速得到系统的初始模型,然后利用PEM方法进一步优化模型参数。

预测误差法是极大似然参数估计法的一种推广,不同之处在于它不要求获得数据概率分布的先验知识[13]。PEM采用k时刻之前的输入输出信号计算k+1,直到将来时刻的输出。在给定观测量z(k)后,调整参数η使预报的均方误差达到最小。预测误差模型见式(2):

z(k) =f[z(k-1),…,z(1),z(0),

u(k-1),…,u(1),η]+e(k)

=f[zk-1,uk-1,η]+e(k)

(2)

z(k)的条件数学期望即其“最佳”预测,即满足式(3):

(3)

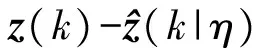
J(η)=lg detD(η)

(4)

并且满足式(5):

(5)

通过极小化J(η)来获得预报误差估计量。

本文采用的辨识方法如下:

(1)首先,选取式(1)子空间法的待辨识模型,采用子空间算法得到系统的初始模型。本文应用的子空间辨识方法推导及算法见文献[14]。

(2)考虑到无人直升机的线性化方程对结构有所要求,因此限定式(1)中由子空间算法得到的初始模型中A,B的部分参数值(如0,1),然后将该模型作为PEM算法的初始状态进行辨识,该方法可大大提高辨识的准确度。

3 试验验证

试验所采用的无人直升机为单旋翼带尾桨直升机,以其线性时不变模型作为辨识对象,辨识无人直升机在低空巡航下的模型参数。无人直升机动力学模型的输入和输出是通过操作员的控制指令数据,以及机载传感器采集飞机飞行状态数据获得的,数据的采样频率为50 Hz。

3.1 数据预处理

为了准确地辨识模型参数,同时避免将系统的噪声引入模型,需要对获得的飞行数据进行滤波处理。鉴于无人直升机飞行数据中的噪声绝大部分位于高频段,而其主要模态的固有频率一般处于5 Hz的中低频段,所以需要对辨识数据进行低通滤波,以消除输出信号中噪声带来的高频成分,优化辨识效果。本文采用的低通滤波器为截止频率为8 Hz的4阶巴特沃斯低通滤波器。

3.2 辨识结果

运用子空间方法辨识得到的无人直升机线性模型参数A,B见式(6)和式(7)。将动力学模型预测的输出和实际飞行的测量数据进行对比，验证辨识所得模型的有效性。对比结果如图1～图3所示,图中,实线表示实测输出,虚线表示预测输出。

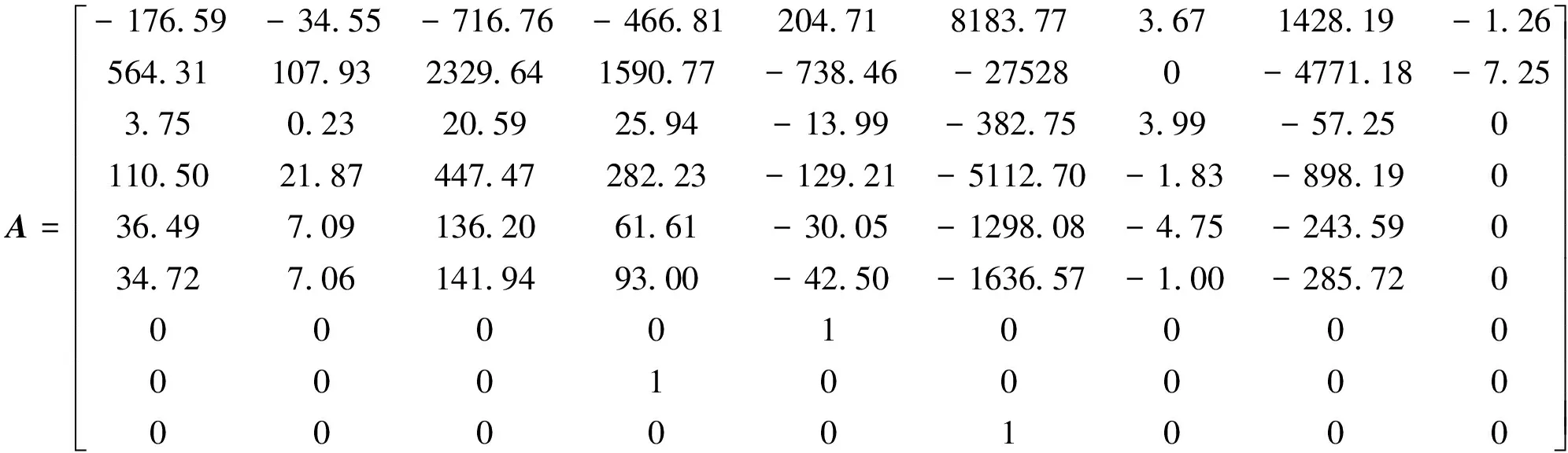
(6)

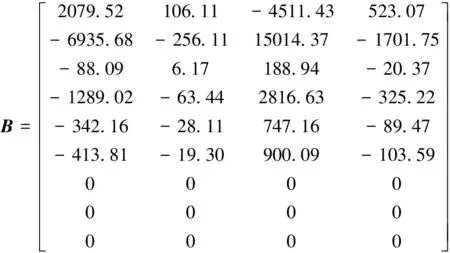
(7)

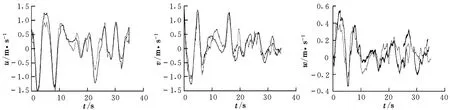
图1 u,v,w的实测值与预测值对比Fig.1 Comparison between flight data and predicted data of u,v,w

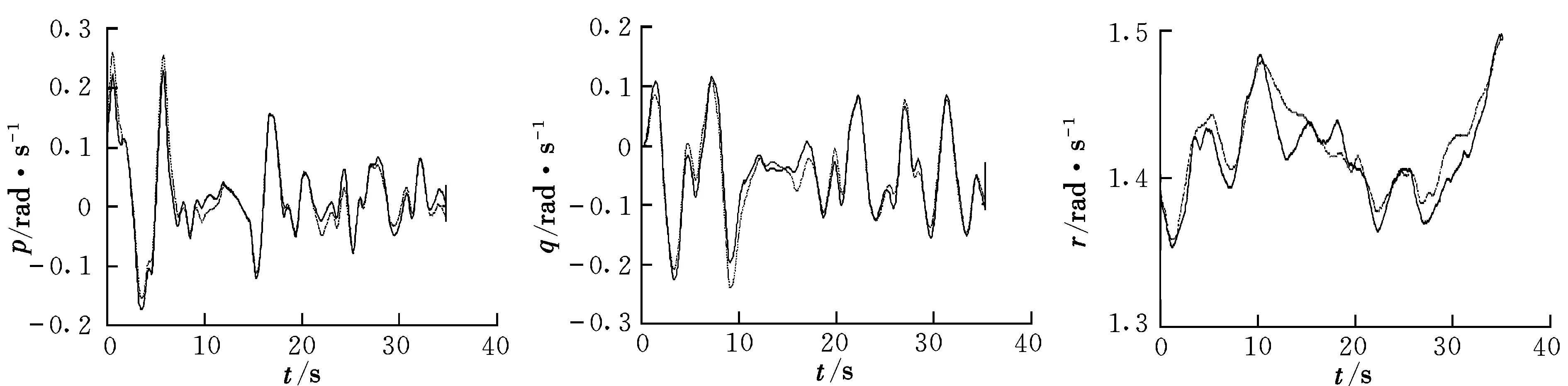
图2 p,q,r的实测值与预测值对比Fig.2 Comparison between flight data and predicted data of p,q,r

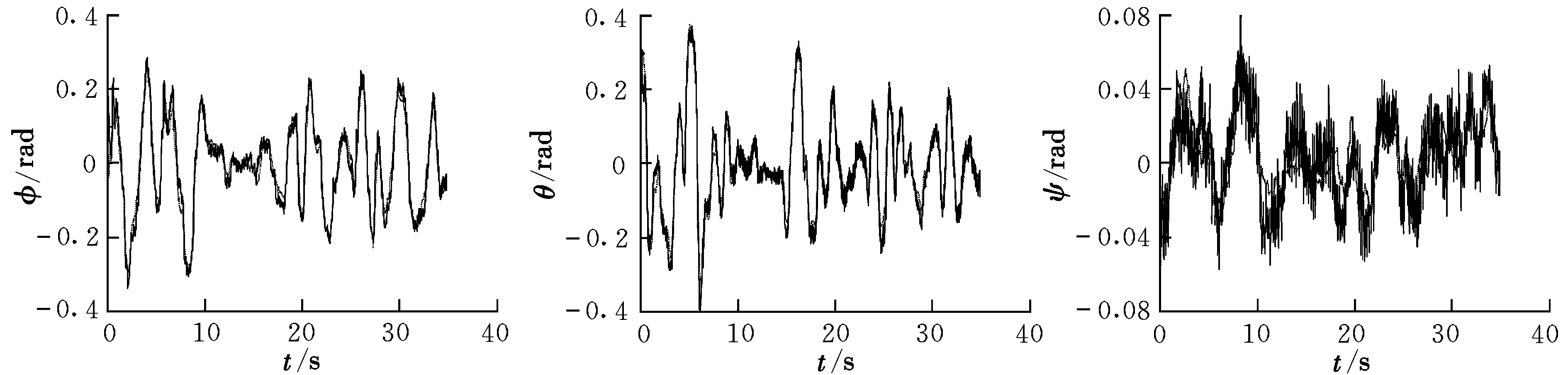
图3 φ,θ,ψ的实测值与预测值对比Fig.3 Comparison between flight data and predicted data of φ,θ,ψ

为了定量表示实测值与辨识结果的相符程度,本文引入指标EBF,其计算方法如式(8)所示:

(8)

通过分析实际飞行数据与辨识模型输出对比图像以及参数EBF表可以看出,辨识得到的模型能够准确地预测俯仰角、俯仰角速度、滚转角以及滚转角速度;但在预测偏航角速度以及偏航角时,预测结果与实际测量结果有较大偏差。造成该现象的主要原因是由于航向测量的传感器精度不够。

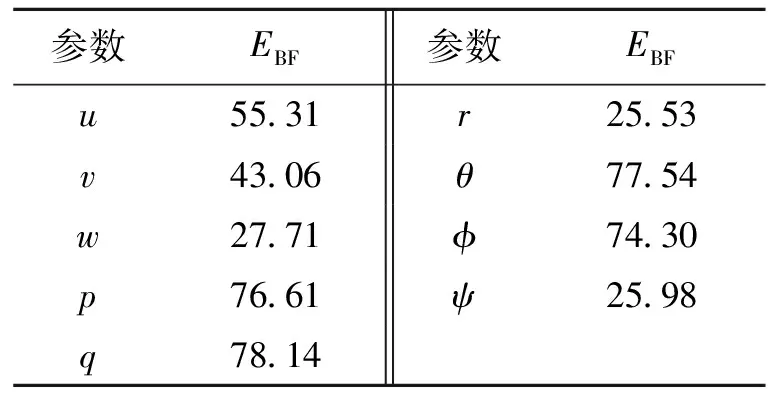
表1 参数的相符程度Table 1 Matching degree of parameters

4 结束语

本文在分析子空间辨识方法和预测误差法优缺点基础上,给出了一种两阶段辨识方法,并将其用于无人直升机辨识,辨识结果证明了方法的有效性。文中采用的辨识方法可以推广到其它飞行器(如固定翼飞机)模型参数的辨识。

[1] 杨一栋.直升机飞行控制[M].北京:国防工业出版社,2007:72-79.

[2] 王琨玉.直升机飞行控制系统[M].北京:蓝天出版社,1999:92-98.

[3] 孙涛.直升机飞行力学模型辨识研究[D].南京:南京航空航天大学,2010.

[4] 宋彦国,孙涛.旋翼飞行器飞行力学系统辨识建模算法[J].南京航空航天大学学报,2011,43(3):387-392.

[5] 吴建德,李平,韩波.一种基于参数辨识的微小型无人直升机建模方法[J].航空学报,2007,28(4):845-850.

[6] 杨帆,熊笑,陈宗基,等.超小型直升机动力学模型的建模、辨识与验证[J].北京航空航天大学学报,2010,36(8):913-917.

[7] 孙涛,宋彦国,张呈林.基于子空间法的小型直升机飞行力学模型辨识[J].南京航空航天大学学报,2008,40(5):589-593.

[8] 李幼凤,苏宏业,褚健.子空间模型辨识方法综述[J].化工学报,2006,57(3):473-479.

[9] Metter Bernard,Mark B Tischler,Takeo Kanade.System identification of small size unmanned helicopter dynamics[J].Journal of the American Helicopter Society,2002,47(1):50-63.

[10] Metter B.Modeling small-scale unmanned rotor-craft for advanced flight control design[D].Pittsburgh:Camegie Mellon University,2001.

[11] 孙涛,宋彦国,张呈林.模型直升机悬停状态下飞行力学模型辨识[J].航空学报,2009,30(1):40-45.

[12] 沈福生.小型无人直升机飞行力学参数化模型辨识研究[D].南京:南京航空航天大学,2008.

[13] 江群,王道波,李猛.基于PEM的辅助动力装置系统辨识与仿真[J].燃气涡轮试验与研究,2010,23(3):46-49.

[14] Wouter Favoreel, Bart De Moor,Peter Van Overschee.Subspace statespace system identification for industrial processes[J].Journal of Process Control,2000,10(2-3):149-155.

(编辑：李怡)

Two-stageparametersidentificationmethodofunmannedhelicopterbasedonsubspaceandPEM

SHAO Ming-qiang, LI Guang-wen, XU Heng

(College of Automation, Northwestern Polytechnical University, Xi’an 710072, China)

A two-stage identification method is used to study the parameter identification problem of unmanned helicopters, which is derived from the analysis of the advantages and disadvantages of subspace identification methods and prediction error method (PEM). According to this method, the initial parameters of the model are gotten by the subspace method, and the more precise model of helicopters is estimated by the PEM method based on the result of the subspace method. In order to demonstrate the effectiveness of two-stage identification method, a model of a type of unmanned helicopter is identified by the method, and it is shown that its identification precision is good by the comparison between the model output data and the flight data.

unmanned helicopter; subspace; prediction error method; parameter identification

V212.4

A

1002-0853(2013)04-0367-05

2012-12-07;

2013-05-09; < class="emphasis_bold">网络出版时间

时间:2013-06-06 13:21

航空科学基金资助(20125853035)；飞行器控制一体化国防科技重点实验室资助

邵明强(1988-)，男，山东东营人，硕士研究生，研究方向为系统辨识、进化算法；

李广文(1978-)，男，河北献县人，副教授，硕士生导师，研究方向为进化算法、飞行控制技术。