基于hp自适应伪谱法的可调推力最优离轨研究
2013-11-04冯必鸣聂万胜郑刚
冯必鸣, 聂万胜, 郑刚
(装备学院 航天装备系, 北京 101416)
基于hp自适应伪谱法的可调推力最优离轨研究
冯必鸣, 聂万胜, 郑刚
(装备学院 航天装备系, 北京 101416)
根据不同最优化指标要求,利用hp自适应伪谱法,对比分析了固定推力和可调推力制动离轨时的参数变化情况。通过研究发现,以燃料最省为优化指标,采用可调推力制动时,飞行器过渡段飞行时间更长,燃料消耗相对较小;而在时间最短指标要求下,可调推力制动虽消耗大量燃料,但能大大缩短过渡段飞行时间,有利于航天器在执行紧急任务时的快速返回。
hp自适应伪谱法; 固定推力; 制动离轨; 过渡轨道
0 引言
返回式航天器的发展经历了从简单的胶卷舱到复杂航天飞机的漫长历程。长期以来,众多学者根据再入点参数约束开展了固定推力制动离轨最优控制规律的研究,已取得丰硕的成果[1-2]。随着航天事业的发展,空间活动越来越多样化,对航天器离轨/变轨的要求越来越高,使得多种新型轨道机动方式脱颖而出,出现了例如小推力和可调推力作用下航天器空间最优转移轨道[3-4]等问题。目前,大多数文献在解决连续小推力轨道转移[5]时,多采用局部配点法[6](h方法)和全局配点法[7](p方法)求解最优控制问题。上述两种方法单纯采用增加时间分段或增加多项式阶数的方式来调整计算精度,而hp自适应法则是根据计算精度需要,同时调整时间段和多项式的阶数,进而获得更高的计算精度,尤其适合多阶段、状态量变化复杂的最优控制问题求解[8]。
经研究发现,由于连续小推力制动时间过长,在要求航天器快速返回的情况下并不适用。本文受月球登陆器最优控制问题[9]的启发,拟采用hp自适应伪谱法,研究可调推力作用下航天器燃料最省和时间最短离轨情况,寻求既能够满足再入点要求,又能够达到优化指标的离轨制动方式,以满足新的航天任务需要。
1 考虑地球自转的最优制动离轨模型
1.1 飞行器过渡段相对运动方程
根据地球自转时飞行器相对于惯性坐标系的关系,建立以相对参数表示的飞行器制动离轨运动方程[10]:
dR/dt=Vsinγ
dθ/dt=Vcosγsinψ/(Rcosφ)
dφ/dt=Vcosγcosψ/R
dV/dt=Tcosαcosβ/M-grsinγ-gφcosγ×
cosψ+ω2Rcosφ(sinγcosφ-
cosγsinφcosψ)
dγ/dt= (1/V)[Tsinα/M+V2cosγ/R-
grcosγ+gφsinγcosψ+
2ωVcosφsinψ+ω2R×
cosφ(cosγcosφ+sinγsinφcosψ)]
dψ/dt= (1/V)[Tcosαsinβ/(Mcosγ)-
V2cosγsinψtanφ/R-gφsinψ/cosγ+
2ωV(cosφtanγcosψ-sinφ)-
ω2Rsinφcosφsinψ/cosγ]
dM/dt=-T/Ve
式中,状态参数R,θ,φ,V,γ,ψ分别为地心距、经度、纬度、相对速度、相对倾斜角(与当地水平线夹角,下偏为负)和相对航向角(以正北方向开始度量,右偏为正);控制参数α,β,T分别为推力角、推力偏角以及推力大小;ωe为地球自转角速度。
1.2 最优控制问题求解
1.2.1 一般优化问题描述
本文应用Radau伪谱法求解最优控制问题,为不失一般性,考虑Bolza形式的最优控制,具体形式见文献[11]。
1.2.2 hp自适应更新方法
将整个优化过程划分为K个时间段,每个时间段内的配点数量为Nk,自适应算法在每一时间段内设定一个离散状态方程和路径约束的最大误差值εd,如果每个时间段内的计算精度大于εd,则对整个过程重新划分。划分方法有两种:一是增加每个时间段内Lagrange多项式的阶数;二是增加时间分段的数量[11]。
在前1~(K-1)个时间段内采用Nk阶多项式近似表示控制变量:
由于最后一个时间段K的最后一个点不属于LGR配点,因此,在第K个时间段内的控制变量采用Nk-1阶多项式近似表示为:
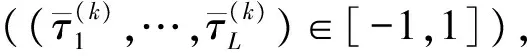
式中,l=1,…,L。

(1)更新方式确定
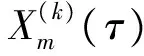
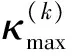
事先设定一个曲率阈值rmax,如果rk
(2)每个时间段内Lagrange多项式阶数的确定
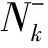
式中,X为任意常数,控制每一段内配点数的增长情况。
(3)每一时间段内重新分段数目的确定
设第k个时间段内重新划分的段数为nk,则可用下式[12]表示:
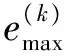
式中,Y为任意常数,控制段数的增长情况。
2 典型事例验证
根据文献[1]提供的标准航天飞机过渡段飞行参数,验证优化方法的可行性。结果如图1所示。
航天飞机制动时高度为280 km,质量为88 000 kg,相对速度为7 363 m/s,倾斜角为0.011°,由两台推力为26 000 N的轨控发动机提供制动力,发动机燃气出口速度为3 000 m/s;制动结束时质量为84 870 kg,高度为122 km,再入相对速度为7 453 m/s,再入倾斜角为-1.604°。本文根据燃料最省的要求计算得到航天飞机再入时的相对速度为7 452 m/s,再入倾斜角为-1.6°,燃料消耗为3 000 kg。计算结果说明该方法在研究最优制动离轨问题时是可行的。
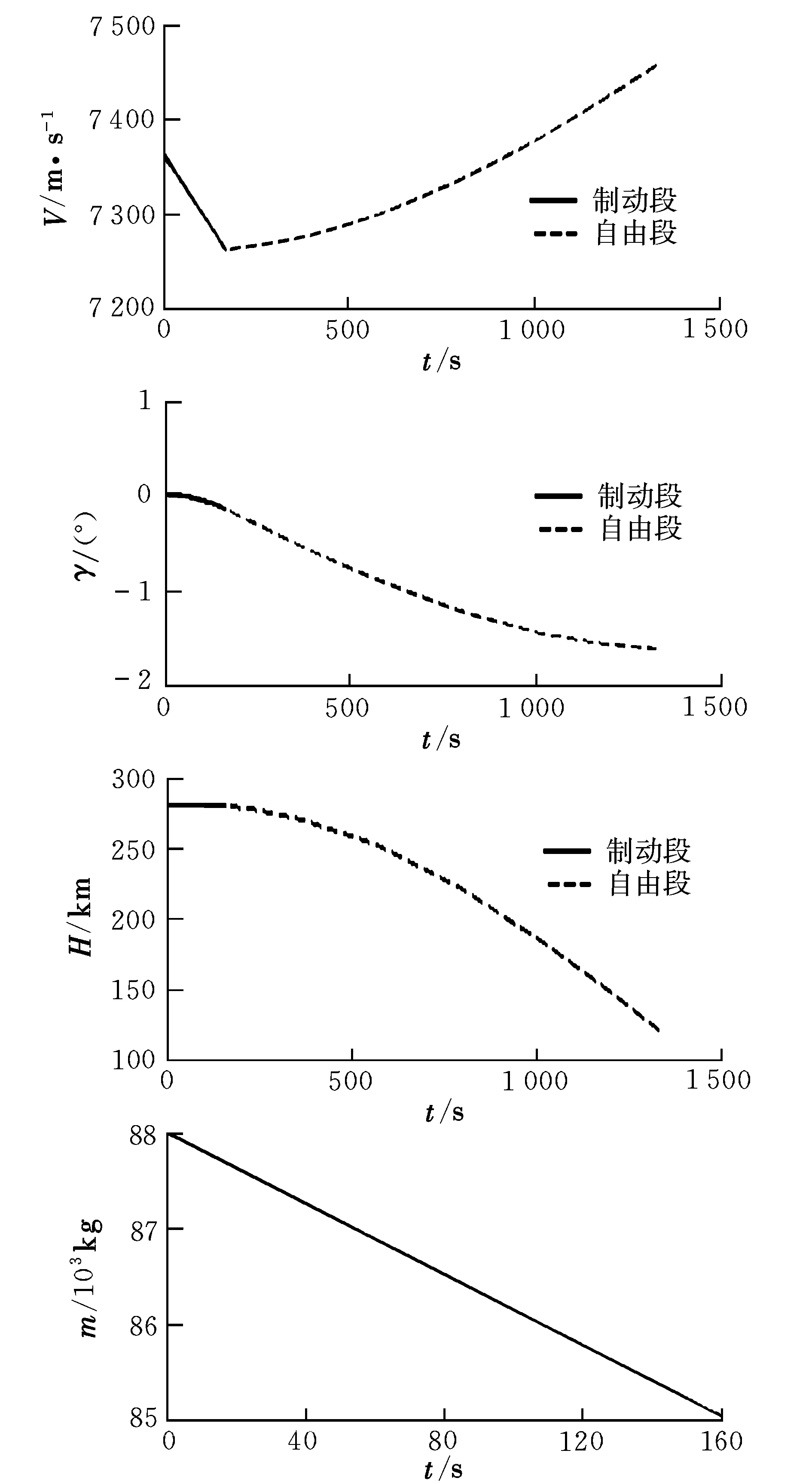
图1 航天飞机燃料最省飞行参数变化情况Fig.1 Flight parameters of space shuttle in minimal fuel consumption
3 不同制动方式对比分析
不考虑发动机侧向作用的情况下(即β=0°),以单台推力为2 500 N,真空比冲为2 930 N·s/kg的轨控发动机为例,假设推进舱总共4台发动机,分别针对5 000 N,10 000 N固定推力和5 000 N,10 000 N变推力研究总质量3 000 kg的飞行器在燃料最省和飞行时间最短两种条件下,不同推力制动离轨时主要参数的变化情况。
3.1 燃料最省方案
图2所示为固定推力制动和可调推力制动两种情况下,过渡段飞行速度、倾斜角的对比情况。从图中不难看出,两种制动方式都能够使再入点指标参数达到期望值,但是采用可调推力制动时,过渡段飞行轨迹更为平缓,飞行时间较固定推力制动时长250 s以上。
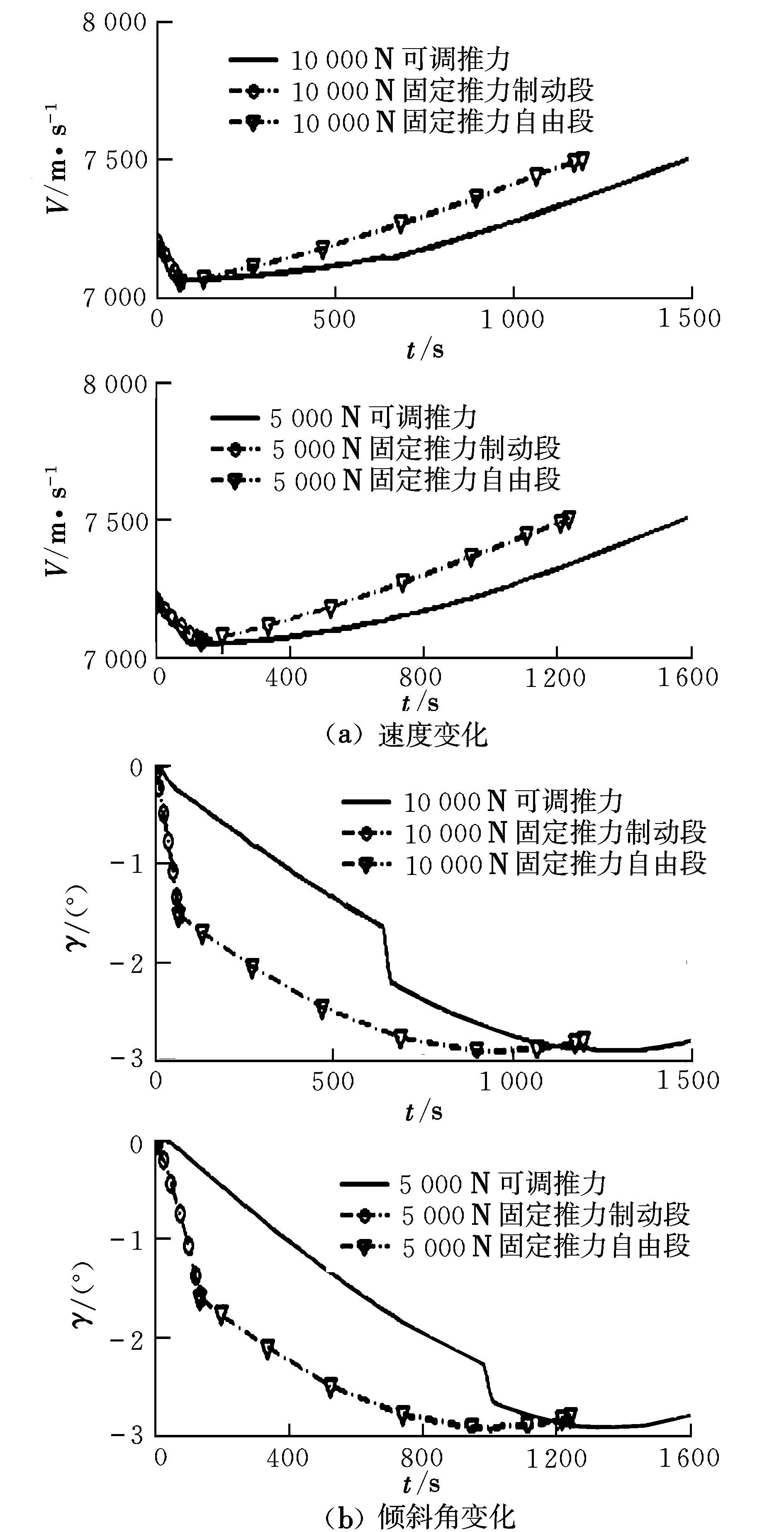
图2 燃料最省条件下飞行参数对比Fig.2 Comparison of flight parameters in minimal fuel consumption
从图2所示不同制动方式下速度和倾斜角的对比中发现,在燃料最省条件下,两种制动方式得到的速度都呈现出先减小再增大的变化规律,而且倾斜角的变化趋势也基本一致。不同的是,可调推力制动时,初期倾斜角变化比较平缓,而在后半段出现明显的折点,这是由于轨控发动机再次工作,使倾斜角在短时间内发生较大改变。图3为可调推力制动时飞行器总体质量、推力角和推力变化情况。
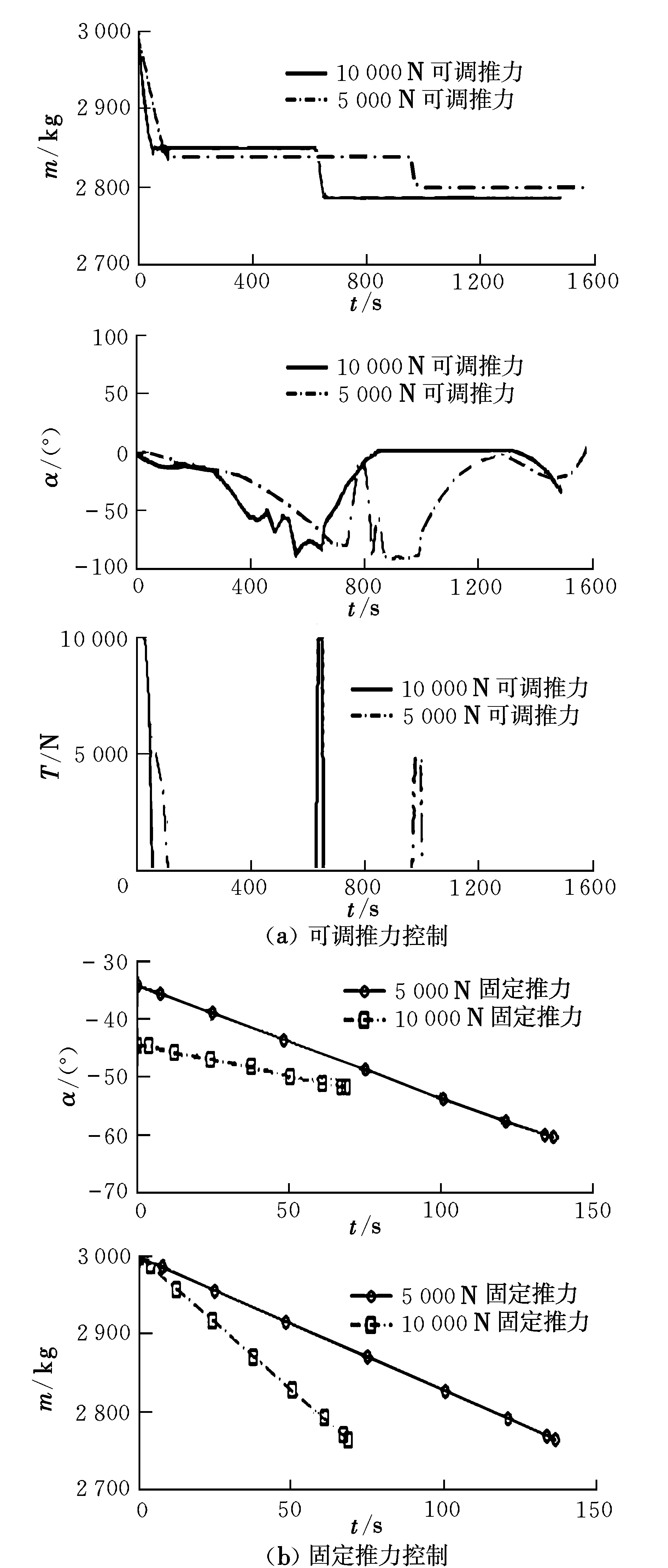
图3 燃料最省条件下控制量和质量对比Fig.3 Comparison of control parameters and mass in minimal fuel consumption
从图3(a)可知,轨控发动机进行了两次点火,两次点火作用时,推力角均采用线性变换,虽然在两次点火间计算得到的推力角变化复杂,但是由于两次点火之间没有推力作用,推力角可在较长时间内采用线性规律转换到需要的状态。对比图3(b)所示固定推力制动时的变化情况不难看出,采用可调推力制动时,燃料消耗相对较小,以最大推力10 000 N为例,采用可调推力制动时燃料消耗较固定推力制动要节省30~40 kg。
3.2 时间最短方案
图4为可调推力制动和固定推力制动两种条件下,过渡段飞行速度、倾斜角变化的对比情况。与燃料最省时的变化情况不同,最短时间要求下,可调推力制动时的速度先增大后减小,而燃料最省和传统固定推力制动时的速度变化都是先减小后增大;而且可调推力制动时,初期倾斜角变化较快,过渡段飞行轨迹较陡。
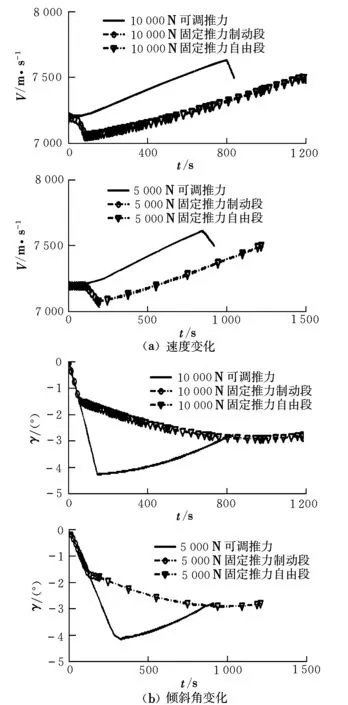
图4 时间最短条件下飞行参数对比Fig.4 Comparison of flight parameters in shortest time condition
通过与固定推力制动的情况相比较不难看出,可调推力制动时,过渡段飞行时间明显小于固定推力制动时的情况。固定推力制动时过渡段飞行时间至少需要1 200 s,而可调推力制动时过渡段飞行时间为800 s,大大缩短了过渡段飞行时间。
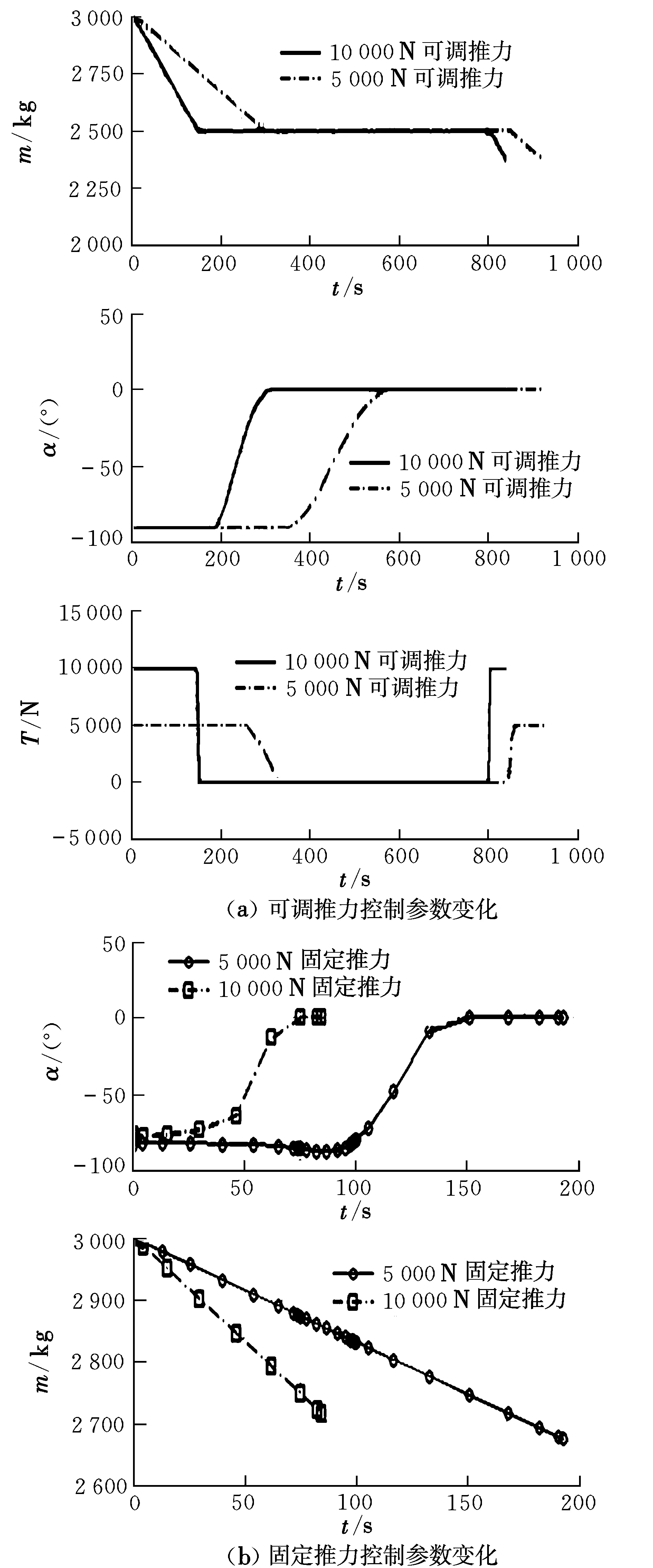
图5 时间最短条件下控制量和质量对比Fig.5 Comparison of control parameters and mass in shortest time condition
图5为两种推力制动时控制参数的变换情况。可调推力制动时,首先以最大推力沿速度垂直方向改变倾斜角,使飞行器以较大倾斜角加速离轨,并在第二次点火作用时,以最大推力沿速度反方向制动,快速减小再入速度,以达到指定的再入参数;固定推力制动时,大推力发动机的工作时间较短,而且两次点火制动几乎都采用最大推力的作用形式;而推力较小时,第一次点火作用后期有一段推力逐渐减小的过程,对于发动机的调节能力要求较高。虽然可调推力制动可以大大缩短飞行器过渡段飞行时间,但是燃料消耗量也随之增加,全过程消耗燃料约625 kg,比固定推力制动多消耗近300 kg燃料。
4 结束语
通过本文研究发现,利用hp自适应伪谱法解决可调推力制动离轨的多阶段最优控制问题是可行的,并且采用可调推力发动机制动离轨时,在节省燃料方面并没有太大优势,而且过渡段飞行时间较固定推力制动时更长;在减小过渡段飞行时间方面,可调推力制动的优势十分明显,适用于航天器快速返回的情况,虽然快速离轨时燃料消耗较大,但能够较大幅度地缩短过渡段飞行时间;无论是要求燃料最省还是飞行时间最短,采用可调推力制动离轨,发动机都进行了多次点火,这样能够增强飞行器外层空间过渡段飞行的隐蔽性,增加轨迹的预测难度。
[1] David Heath,Lazarus Gonzales.OFT-1 reference flight profile deorbit through landing[R].Houston Texas:National Aeronautics and Space Administration,1977.
[2] Baldwin M C,Pan Binfeng,Lu Ping.On autonomous optimal deorbit guidance[R].AIAA-2009-5667,2009.
[3] 李艳艳,任凌.地球同步卫星的小推力离轨最优控制[J].系统仿真学报,2010,22 (1):96-98.
[4] Wu Baolin,Wang Danwei,Poh Eng Kee.Nonlinear optimization of low-thrust trajectory for satellite formation:legendre pseudospectral approach[J].Journal of Guidance,Control,and Dynamics,2009,32 (4):1371-1381.
[5] 胡正东.天基对地打击武器轨道规划与制导技术研究[D].长沙:国防科学技术大学,2009.
[6] Kameswaran S,Beigler L T.Convergence rates for direct transcription of optimal control problems using collocation at radau points[J].Computational Optimization and Applications,2008,41 (1):81-126.
[7] Benson D A,Huntington G T,Thorvaldsen T P,et al.Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1435-1440.
[8] Galvao A,Gerritsma M,Maerschalk B D.hp-Adaptive least-squares spectral element method for hyperbolic partial differential equations[J].Journal of Computational and Applied Mathematics,2008,215(2):409-418.
[9] 彭祺擘,李海阳,沈红新.基于高斯-伪谱法的月球定点着陆轨道快速优化设计[J].宇航学报,2010,31 (4):1012-1015.
[10] 吴德隆,王小军.航天器气动力辅助变轨动力学与最优控制[M].北京:中国宇航出版社,2006:39-42.
[11] Darby C L,Hager W W,Rao A V.A preliminary analysis of a variable-order approach to solving optimal control problems using Pseudospectral method[R].AIAA-2010-8272,2010.
[12] Zhao Y J.Optimal pattern of glider dynamic soaring[J].Optimal Control Applications and Methods,2004,25(2):67-89.
Optimaldeorbitresearchofspacecraftwithvariablethrustbasedonhp-adaptivepseudospectralmethod
FENG Bi-ming, NIE Wan-sheng, ZHENG Gang
(Department of Space Equipment, Academy of Equipment, Beijing 101416, China)
Considering different optimal objects, the hp-adaptive pseudospectral method was used to analyze the comparison of flight parameters when the vehicle deorbit with the control of fixed thrust and variable thrust. The results showed that with the index of minimal fuel, using variable thrust would take more time during transition than using fixed thrust, and could economize little fuel; however, with the index of shortest time, variable thrust could shorten the flying time obviously during transition by consuming more fuel, and was propitious to the spacecraft rapid return with emergency missions.
hp-adaptive pseudospectral method; fixed thrust; deorbit; transition orbit
V448.2
A
1002-0853(2013)04-0354-05
2012-11-19;
2013-03-21; < class="emphasis_bold">网络出版时间
时间:2013-06-06 12:24
冯必鸣(1984-),男,四川泸州人,博士研究生,研究方向为飞行器轨迹优化与制导。
(编辑:方春玲)
