四旋翼无人机反馈线性化多指标控制设计

柯艺杰, 周江华, 王生

(1.中国科学院大学 材料科学与光电技术学院, 北京 100094; 2.中国科学院 光电研究院 浮空器研发中心, 北京 100094)

四旋翼无人机反馈线性化多指标控制设计

柯艺杰1,2, 周江华2, 王生2

(1.中国科学院大学 材料科学与光电技术学院, 北京 100094; 2.中国科学院 光电研究院 浮空器研发中心, 北京 100094)

针对四旋翼无人机,提出了一种基于反馈线性化的非线性控制方法。该方法在实现姿态、位置控制的同时,能够有效地解决控制系统的奇异点问题,并能实现速度和加速度等状态量的上限保护。另外,针对无人机鲁棒性、抗干扰性能和动态性能等多指标综合问题,采用了凸集成设计思路,实现了各通道多指标性能之间的平衡。仿真结果证明了在输入饱和约束下,控制器设计的有效性。

四旋翼无人机; 反馈线性化; 多指标; 凸集成设计

0 引言

四旋翼无人机由于具有垂直起降、操纵敏捷性高等优势,在军用、民用等领域有着很广阔的应用前景,可用于环境监测、灾后救援和战场侦察等场合,因而近年来受到很多研究学者的关注,并且成为未来微型无人机的主要构型之一[1]。

四旋翼无人机是一个高度非线性耦合的欠驱动系统,其控制系统一般需要满足[2]:(1)一定的稳定性、鲁棒性和需要的动力学特性;(2)非线性处理能力;(3)能适应参数变化和环境干扰。

非线性控制方法相对线性控制方法能够大大地拓展四旋翼无人机的工作空间。近年来,这方面的研究层出不穷,例如:A Mokhtari[2]提出了一种精确线性化和滑模观测器的综合方法,并加入了自适应估计器,能够确定外界干扰的影响;T Madani[3]提出了全状态反步控制方法,将系统控制分解成为三个子系统,实现了整体控制的稳定;G V Raffo[4]验证了非线性H∝和反步综合控制方法在环境干扰和参数不稳定性下具有鲁棒性;O Purwin[5]设计了一种迭代学习方法,通过经验学习,能够在线控制姿态的快速转换等。尽管如此,文献中仍缺乏对四旋翼无人机状态的安全控制,比如下降加速度等,同时在多指标性能的平衡上缺乏相对量化的设计思路,大部分文献针对的是特定的性能设计。

鉴于此背景,本文针对四旋翼无人机提出了一种基于反馈线性化的非线性控制方法。方法除了实现基本的姿态和位移控制外,还能够有效地解决控制中的奇异点问题,控制系统的工作状态,同时,本文还针对鲁棒性、抗干扰性能和动态性能多指标性能的综合问题,对各通道进行了凸集成设计。

1 动力学模型

1.1 坐标系定义

定义系统惯性坐标系和机体坐标系如图1所示,惯性坐标系采用北东地系。

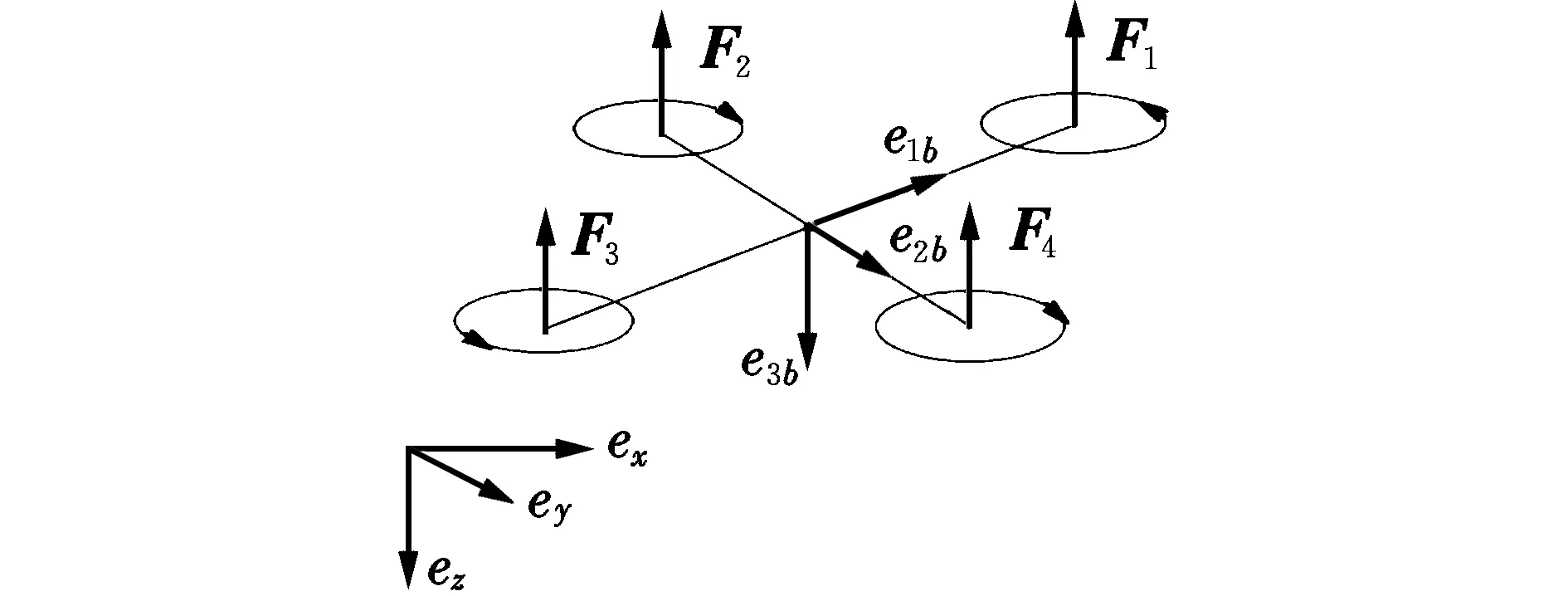
图1 四旋翼无人机坐标系定义Fig.1 Definition of quadrotor coordinate systems

1.2 动力学方程

系统动力学方程包括机体动力学方程和旋翼电机动力学方程两部分。

1.2.1 机体动力学方程

根据刚体动力学的基本原理,有:

式中,ξ为惯性系坐标;v为惯性系速度;g为重力加速度;m为全机质量;T为旋翼总推力;R为姿态角转换矩阵;Faero为空气摩擦力;If为机体系惯性矩阵;Ωb为机体系角速度;Ga为陀螺力矩;Γa为旋翼反力矩;Taero为空气摩擦力矩。

1.2.2 旋翼电机动力学方程

对于低电感的电机,旋翼电机的动力学模型为[6]:

式中,Jr为旋翼惯性矩;ωi为电机转速;ks为摩擦阻力矩;km为电机力矩常数;ke为EMF常数;kr为空气阻力矩常数;ui为输入电压。

2 反馈线性化控制

2.1 基本算法设计

系统动力学方程为:

控制设计思路先以高度和姿态角为控制对象,目标输出为:

按反馈线性化原理[7],可以得到动力学系统的相对阶为3,并有以下形式:

令h(X)各阶导数为零,可以得到外部输出稳定时旋翼转速均为平衡时的状态,系统零状态稳定。

对于平移方向的控制,由系统动力学方程可以得到x,y和俯仰倾转角φ,θ的直接非线性映射关系。

然后根据线性系统设计方式建立名义控制系统:

2.2 奇异点控制和状态上限保护

2.2.1 奇异点控制

det[LgLfh(X)]=

Jrqω1ω3(ω2-ω4)+4CFlω1ω2ω3ω4]}

2.2.2 状态上限保护

(1)下降控制

(2)大姿态角控制

针对实际飞行中可能出现的大姿态角(滚转和俯仰)安全问题,设置上限为:φ,θ≤TV3。当φ,θ>TV3时,取φd=sgnφdTV3,θd=sgnθdTV3。

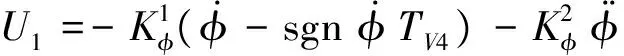
使滚转、俯仰角速度幅值趋向于TV4。

3 多指标集成设计

3.1 俯仰和倾转子系统的设计

俯仰和倾转系统经反馈线性化之后,为三阶子系统,其形式如图2所示。图中,v为控制输入;y为输出值;d,η分别为加速度和速度干扰信号;K(s)为控制器。

图2 俯仰、倾转三阶子系统示意图Fig.2 Schematic diagram of pitch and roll third-order subsystems

3.1.1 鲁棒特性设计

=AX+B1ω+B2u

输出值

系统鲁棒性能可以用无穷大范数表示为:

‖Hy1ω‖∞=‖C1(sI-A-B2K)-1B1‖∞

采用控制器形式

柴油机单位功率燃油消耗是衡量柴油机经济性的重要指标，可通过监测主机燃油消耗量和曲轴扭矩计算所得。柴油机燃油的燃烧效率直接决定油耗率的大小，但并不是影响实际所测得油耗率的唯一因素。燃油流量计通常装设在供油单元，其后还要依次通过高压油泵和喷油器等设备后进入柴油机缸内燃烧，这些设备的泄漏故障也会导致计算所得燃油消耗率的上升。综上所述，燃油消耗率能够作为柴油机故障诊断的有效参考依据，以便及时排除故障,并保障船舶安全并提高其经济性能。[10]

K(s)=K0+K1s+K2s2

利用遗传算法在Ki∈[0,300](i=0,1,2)范围内搜索优化解,约束条件为:K0/K1>1,K0/K2>10,以表征抑制速度和加速度误差的干扰。运行得到的优化解为:K0=236.316,K1=118.158,K2=23.632,相应的最优鲁棒性能为2.651 67。

3.1.2 干扰抑制特性

d干扰模型和η干扰模型分别如图3和图4所示。

图3 d干扰模型示意图Fig.3 Schematic diagram of d disturbance model

图4 η干扰模型示意图Fig.4 Schematic diagram of η disturbance model

图中,Gd=1/s2,Hd=-(K0+K1s+K2s2)(1/s),Gη=1/s,Hη=-(K0+K1s+K2s2)(1/s)。

以干扰阶跃信号响应降至5%峰值所用时间作为干扰性能指标,以此表征四旋翼无人机抵抗常值干扰的能力。

3.1.3 集成设计

通过调试,选取两个样本。样本1:K0=236,K1=118,K2=23;样本2:K0=300,K1=120,K2=20。样本性能和目标性能见表1。

表1 样本性能和目标性能Table 1 Table of sample performance and target performance

其中,d干扰性能两个样本均满足要求,故只需对鲁棒性能和η干扰性能进行集成设计。根据凸集成设计原理,取λ1=0.46,λ2=0.54。

以此对样本1和样本2进行合成:

式中,Ks1(s),Ks2(s)分别代表样本1和样本2的控制器。利用Pade近似方法降阶得到合成后K(s)

控制器的简化形式为:

Ksyn(s)=

321.8745+116.8444s+21.38s2+

相应的鲁棒性能为2.9642,d干扰性能为1.12 s,η干扰性能为1.2 s。

3.1.4 动态性能设计

对于通道的动态性能,采用前置环节以调节系统的阻尼比,如图5所示。

图5 带前置环节的动态性能示意图Fig.5 Schematic diagram of dynamic performance with pre-links

利用3.1.3节得到的Ksyn(s)控制器,测试得到阶跃响应动态性能为:超调量为18%,5%误差稳定时间为0.433 s,超调量过大。当Ke1=0.2,Ke2=0.11时,系统动态性能为:超调量为1%,5%误差稳定时间为0.223 s,达到了设计指标要求。至此,完成了俯仰倾转子系统的集成化设计。

3.2 其他通道设计

对于其他通道,同样采用类似方法,得到各通道的控制器和性能指标如表2所示。

4 仿真结果及分析

针对设计的控制器,以输入11 V电压作为输入饱和限制,考察四旋翼无人机的位置跟踪性能。设定初始位置为(1,-1,1)m,初始姿态角为(0,0,-1)rad,目标位置为(0,0,0)m,目标姿态角为(0,0,0)rad。在俯仰和滚转通道加入幅度为[-0.5,0.5] rad/s2的随机加速度信号,并在15 s加入幅度为5 rad/s2、持续时间为0.2 s的脉冲俯仰加速度干扰。各响应曲线如图6～图10所示。由图可以发现,系统在饱和约束和外在干扰下工作良好,各通道表现出类似线性系统的性能,并且对z向加速度实现了较好的约束控制(设定上限为1 m/s2),保证了飞行的安全性。

图6 位置响应曲线Fig.6 Curve of position response

图7 姿态角响应曲线Fig.7 Curve of attitude response

图8 电机输入电压响应曲线Fig.8 Curve of motor inputs response

图9 电机转速响应曲线Fig.9 Curve of motor speed response

图10 z向加速度响应曲线Fig.10 Curve of z acceleration response

5 结论

针对四旋翼无人机,提出了一种基于反馈线性化的非线性控制方法,该方法能够实现正常姿态和位置控制,方法的优点在于:

(1)能够有效避免系统奇异点问题;

(2)能够有效控制系统重要状态量如加速度、大姿态角等,实现飞行的安全保护;

(3)面对设计的多指标性能要求,针对解耦后相对独立的各通道进行了凸集成化设计,避免了性能调节的盲目性,为设计提供了一种量化方法。

未来的工作方向是进一步考察饱和输入对系统姿态调节以及路径跟踪的影响。

[1] Kumar V,Michael N,Opportunities and challenges with autonomous micro aerial vehicles[J].The International Journal of Robotics Research,2012,31(11):1279-1291.

[2] Mokhtari A,Benallegue A,Orlov Y.Exact linearization and sliding mode observer for a quadrotor unmanned aerial vehicle [J].International Journal of Robotics & Automation,2006,21(1):39-49.

[3] Madani T,Benallegue A.Control of a quadrotor mini-helicopter via full state backstepping technique[C]//Decision and Control,45th IEEE Conference on.IEEE,2006:1515-1520.

[4] Raffo G V,Ortega M G,Rubio F R.An integral predictive/nonlinear H(infinity) control structure for a quadrotor helicopter[J].Automatica,2010,46(1):29-39.

[5] Purwin O,D’Andrea R.Performing aggressive maneuvers using iterative learning control[C]//Robotics and Automation,ICRA’09,IEEE International Conference on.IEEE, 2009:1731-1736.

[6] Bouabdallah S,Murrieri P,Siegwart R.Towards autonomous indoor micro VTOL[J].Autonomous Robots,2005,18(2):171-183.

[7] Riccardo Marino.非线性系统设计——微分几何、自适应及鲁棒控制[M].姚郁,贺风华,译.北京:电子工业出版社,2006:132-133.

[8] Mistler V,Benallegue A,M’sirdi N K.Exact linearization and noninteracting control of a 4 rotors helicopter via dynamic feedback[C]//Robot and Human Interactive Communication,10th IEEE International Workshop on.IEEE,2001:586-593.

[9] Fu K,Mills J K.The convex integrated design (CID) method:necessary and sufficient conditions for existence of solution[C]//Robotics,Intelligent Systems and Signal Processing,IEEE International Conference on.IEEE,2003:7-12.

[10] Liu H H T,Mills J K.Multiple specification design in flight control system[C]//American Control Conference on.IEEE,2000:1365-1369.

[11] 宋宝泉.小型无人直升机非线性建模与控制算法研究[D].长沙:国防科学技术大学,2010.

FeedbacklinearizationcontrollerdesignforquadrotorUAVwithmultiplespecifications

KE Yi-jie1,2, ZHOU Jiang-hua2, WANG Sheng2

(1.College of Materials Science and Opto-electronic Technology, University of Chinese Academy of Sciences, Beijing 100094, China; 2.Center for LTA System Research and Development, Academy of Opto-electronics, Chinese Academy of Sciences, Beijing 100094,China)

A nonlinear controller based on feedback linearization is proposed for quadrotor UAV in this paper. While realizing attitude and position control, system singularity problem and upper limit protection of states, such as speed and acceleration, can be effectively handled. Furthermore, to solve synthesis problem between multiple specifications of robustness, anti-disturbance and dynamic performance, convex integrated design method is presented to achieve a balance in each channel. The effectiveness of controller design under the constraint of input saturation is verified by numerical simulations.

quadrotor; feedback linearization; multiple specifications; convex integrated design

V249.1; V279

A

1002-0853(2013)06-0516-05

2013-03-25;

2013-07-09; < class="emphasis_bold">网络出版时间

时间:2013-10-22 14:13

柯艺杰(1989-)，男，安徽池州人，硕士研究生，研究方向为飞行器控制。

(编辑：姚妙慧)