气动特性对航天器再入终迹圈的影响研究
2013-11-04胡海龙南英
胡海龙, 南英
(南京航空航天大学 航天学院, 江苏 南京 210016)
气动特性对航天器再入终迹圈的影响研究
胡海龙, 南英
(南京航空航天大学 航天学院, 江苏 南京 210016)
研究了航天器气动特性对其再入飞行的影响,以航天器再入终迹圈范围作为再入飞行能力的特征来预测其最大航程。基于遗传算法的再入飞行轨迹优化,提出了航天器再入终迹圈的数值算法;通过对再入飞行轨迹的数值仿真,得到不同最大升阻比条件下航天器再入终迹圈仿真结果。对再入终迹圈数值结果进行拟合分析,得到最大升阻比与航天器再入飞行最大航程的数值关系,实现了航天器再入航程的预测。
再入航天器; 遗传算法; 再入终迹圈; 升阻比; 数值仿真
0 引言
航天器完成太空任务后从一定轨道高度再入飞行至地面,在过载、气动加热率和航天器结构要求的约束下,优化性能指标,计算出航天器最优再入轨迹[1-6]。满足约束的最优再入轨迹在地球表面上着陆点所组成的闭合轮廓曲线,即航天器再入终迹圈(国内有文献称为覆盖区)[7-9]。
国外学者对航天器再入轨迹优化算法[1-6]、再入终迹圈[7-9]、再入制导律[10]等进行了深入的研究,并且在航天领域得到了实际的应用[11-12]。国内学者将遗传算法应用于航天器轨迹优化并对其应用进行了分析和探讨[13-14]。航天器轨迹优化的传统算法主要有基于最优控制理论的间接法[4-5]和采用非线性规划方法的直接法,但无论是直接法还是间接法,由于均采用传统的寻优方法,对初值十分敏感,优化结果的好坏在很大程度上取决于某些优化变量的初始猜测值,因而不便于工程应用。本文采用遗传算法实现航天器再入终迹圈的计算,具有较强的鲁棒性且对初值不敏感。
目前,有关再入终迹圈的研究主要是再入终迹圈的定义及计算方法[9]、再入飞行约束条件及运动模型对航天器再入终迹圈的影响,如最大气动加热率、最大可用过载等对再入终迹圈的影响[7]以及随机干扰(如气动等飞行器模型误差、大气等环境模型误差)对无控再入飞行器终迹圈的影响[8]。由于航天器气动特性决定了航天器的轨道机动能力,影响航天器再入飞行轨迹,从而间接决定航天器的再入终迹圈[7,15]。
本文在航天器再入终迹圈和轨迹优化计算的基础上,通过大量飞行轨迹优化设计的数值仿真及结果分析,研究了航天器气动特性对航天器再入终迹圈的影响,拟合所得到的航天器再入终迹圈和最大升阻比之间的数值关系,用于航天器再入飞行时的航程预测,针对不同的飞行任务对航天器进行最佳的气动外形设计。
1 基本理论
评定航天器升阻特性的重要气动参数是其升阻比K=CL/CD,升阻比主要取决于飞行马赫数和迎角。在马赫数一定的极曲线上,由极曲线原点引出的切线,其切点处对应的升阻比最大,为航天器最大升阻比Kmax。
航天器再入终迹圈定义:航天器从某一初始再入点,在满足所有约束和飞行条件下再入飞行至地球表面时,所能到达的最大着陆区域。即航天器从再入初始时刻t0以飞行状态再入飞行(tf-t0)时间段后,所能到达地球表面的最大着陆区域:
(1)
式中,V为飞行速度;γ为轨迹倾角;ψ为偏航角;H为航天器飞行高度;θ为航天器所在位置经度;φ为航天器所在位置纬度;tf为着陆点时刻。
终迹圈示意图如图1所示。
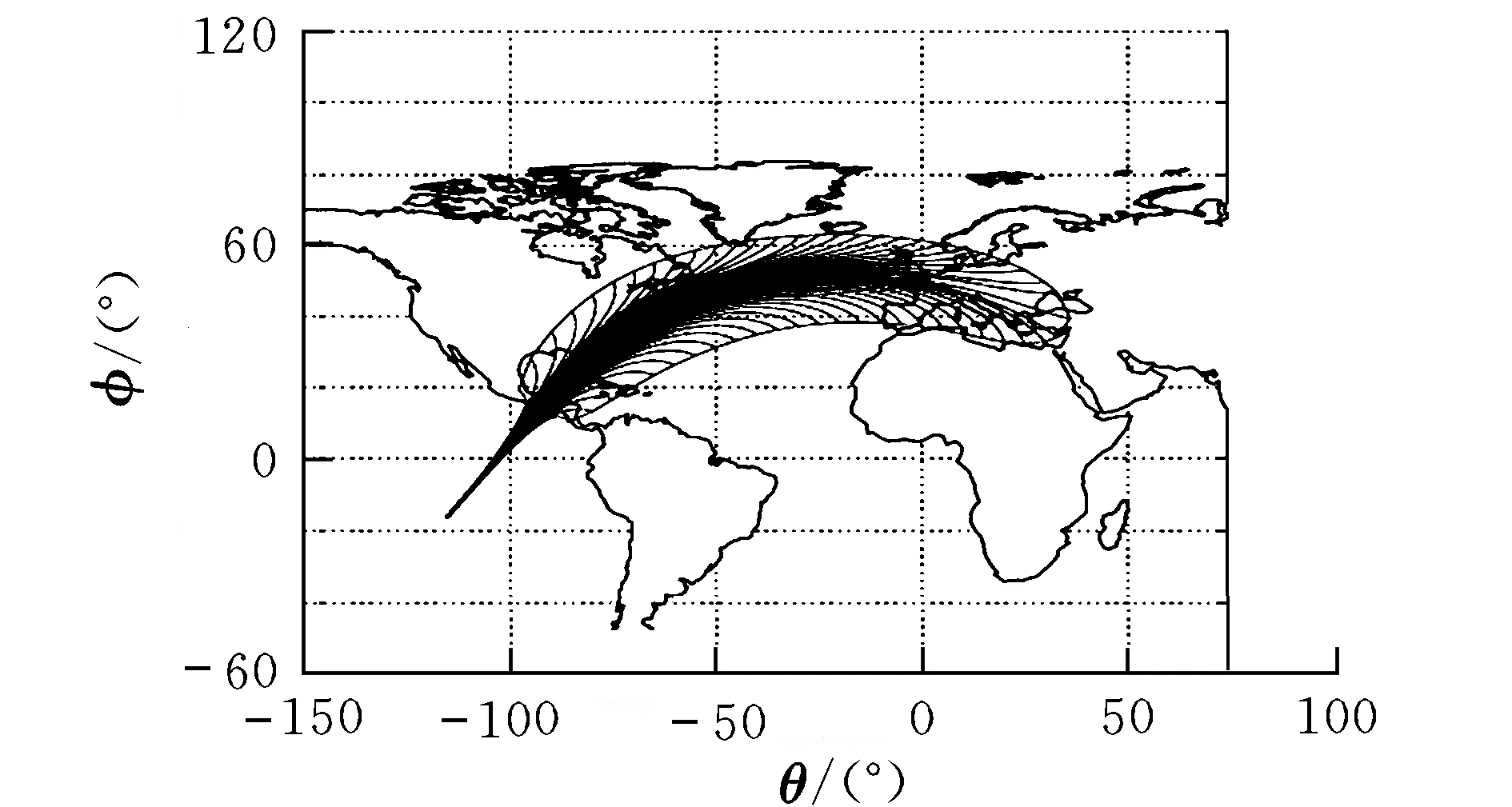
图1 世界地图背景下再入终迹圈示意图Fig.1 Reentry footprint of space vehicle in the background of world map
影响航天器再入终迹圈的主要因素有:航天器升阻比K;再入点初始飞行状态x(t0);再入飞行过程中的约束条件;再入飞行过程中的外界环境(包括随机风场速度VW(θ,φ,H)、加速度aW(θ,φ,H)和大气模型误差,如大气密度误差Δρ(θ,φ,H)和地球引力场误差Δg(θ,φ)等);再入飞行控制律;终端约束。

2 航天器再入动态终迹圈的数值算法
2.1 航天器再入飞行轨迹优化模型
对航天器再入飞行过程做如下假设:将飞船看作运动的质点,飞控系统处于理想工作状态;大气相对地球静止,且同一高度分布均匀;只考虑地球自转,忽略其公转。其再入轨迹方程为:
(2)
式中,S为参考面积;CD,CL分别为阻力系数和升力系数;m为飞行器质量;ρ为大气密度;G为飞船重力加速度;ωe为地球自转角速度;r为地球地心与航天器质心的距离;re为地球半径;x,z分别为经度坐标和纬度坐标;g为地球表面引力加速度。
2.2 航天器再入飞行参考轨迹优化算法
航天器再入轨迹优化可以看作一个多目标优化问题,采用权重系数变换法进行优化求解,即在满足加热率、过载和动压等给定的约束条件下,寻找最优控制律u(t)*(u=[α,σ])使得再入过程中总加热量、总过载和总动压最小。等效的优化问题可以描述为:
X(tf)=Xtf
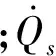
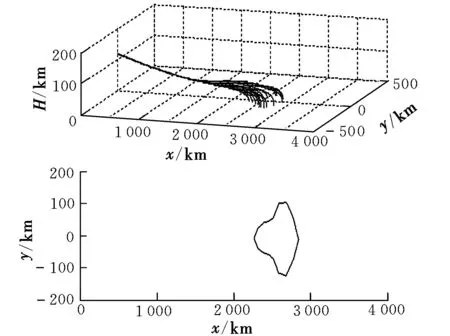
(1)染色体编码:采用直接离散的参数化方法将控制变量u(t)离散。设t∈T,取步长Δt,时间域离散为0=t1 (2)适应度函数设计:采用罚函数处理不等式约束,将约束写入目标函数为: (3) 式中,δshare为小生境半径;dij为解空间上的度量。 (3)确定遗传算子:选择算子采用最优保存策略的选择方式,交叉算子选用单点交叉方式,变异算子采取基本位变异方式。 (4)初始化状态参数,设置遗传算法的基本运行参数,优化得到最优性能再入轨迹S*。 2.3 航天器再入终迹圈计算方法 由2.2中优化得到参考再入飞行轨迹S*,以S*着陆点XtF作为再入终迹圈的计算参考点,在再入参考轨迹优化算法基础上,改变优化目标函数,以再入飞行轨迹着陆点坐标位置与参考点XtF距离最大及再入过程约束总量为优化目标: (4) 将适应度函数改为: F=Cmax+J-[PQ(x)+Pq(x)+Pn(x)] 仿真算例以航天飞机为例,计算参数及其相应约束设置为: S=95 m2,m=20 000 kg ny≤nymax=2.5 α(t)∈[0,30°] σ(t)∈[-30°,30°] tf∈[300,1500] 遗传算法的运行参数为:种群100个,染色体长度30,选择概率0.93,变异概率0.15,运行代数为800代,小生境半径1.6。 3.1 数值仿真结果 航天器再入初始飞行状态为:t0=0 s,V0=7 800 m/s,γ0=-3.74°,ψ0=0°,θ0=1.983 35 rad,H0=120 km,z0=0.016 056 rad。 取Kmax分别为0.5,1.0和1.5,分别对各升阻比下的再入终迹圈进行数值仿真,得到的仿真结果如图2~图4所示。 图2 航天器三维轨迹和再入终迹圈(Kmax=0.5)Fig.2 3-D flight trajectories and reentry footprint (Kmax=0.5) 图3 航天器三维轨迹和再入终迹圈(Kmax=1.0)Fig.3 3-D flight trajectories and reentry footprint (Kmax=1.0) 图4 航天器三维轨迹和再入终迹圈(Kmax=1.5)Fig.4 3-D flight trajectories and reentry footprint (Kmax=1.5) 3.2 仿真结果分析 所有构成再入终迹圈的再入轨迹均满足过载和气动加热约束条件,满足优化所提出的性能指标。随着航天器升阻比的增大,再入走廊宽度也明显增加。当Kmax≤0.5时,为小升阻比半弹道式再入,其机动能力差,纵向和横向最大航程较小,最大纵向和横向航程为几十公里级或者几百公里级;当Kmax≥1.0时,航天器再入方式为滑翔式再入,其机动能力强,纵向和横向最大航程较大。 分别计算Kmax=1.0,1.2,1.4,1.6,1.8和2.0对应的航天器纵向最大航程SL和横向最大航程SH,计算结果如表1所示。 表1 航天器最大升阻比与最大航程的关系Table 1 Relationship between the flying range and Kmax 针对典型的再入初始条件V0=7 800 m/s,γ0=-3.74°,H0=120 km,当Kmax=1.0~2.0时,由表1数据拟合得到最大纵向航程SL和最大横向航程SH与Kmax呈如下函数关系: (7) SH=1600Kmax+900 (8) 该关系式可用于航天器再入飞行时的最大航程的估算预测。 本文研究了航天器气动特性即最大升阻比对航天器再入飞行终迹圈的影响。通过不同升阻比条件下航天器再入终迹圈的数值仿真,得到以下结论: (1)不同升阻比条件下对应的再入终迹圈不同,且随着升阻比增大,航天器再入机动能力增强,对应的再入走廊宽度增加; (2)大升阻比滑翔式航天器再入终迹圈最大纵向航程与航天器最大升阻比的平方呈近似正比关系;最大横向航程与航天器最大升阻比呈近似正比关系。 [1] Lu P.Entry trajectory optimization with analytical feedback bank angle law[R].AIAA-2008-7268,2008. [2] 南英,陈士橹,王志刚.航天器最优再入轨迹的选择分析[J].宇航学报,1996,17(4):105-108. [3] 南英,陆宇平,龚平.登月返回地球再入轨迹的优化设计[J].宇航学报,2009,30(5):1843-1847. [4] 高东迎,岳晓奎.基于区间算法的航天器再入轨迹优化[J]. 科学技术与工程,2012,12(4):853-855. [5] 闵学龙,潘腾,郭海林.载人航天器深空飞行返回再入轨迹优化[J].中国空间科学技术,2009,17(4):9-12. [6] Whitmore S A,Banks D W,Andersen B M,et al.Direct-entry, aerobraking, and lifting aerocapture for human-rated lunar return vehicles [R].AIAA-2006-1033, 2006. [7] Lu Ping,Xue Songbai.Rapid generation of accurate entry landing footprints [R].AIAA-2009-5772,2009. [8] Matney M.Statistical issues for uncontrolled reentry hazards empirical tests of the predicted footprint for uncontrolled satellite reentry hazards[R].NAS-AJSC-CN-24927,2011. [9] Vinh N X.Optimal trajectories in atmospheric flight [R].International Astronautical Federation,International Astronautical Congress,Rome,1981. [10] Xue S,Lu P.Constrained predictor-corrector entry guidance[R].AIAA-2009-5767,2009. [11] 王希季,李颐黎,周其成,等.航天器进入与返回技术[M].北京:中国宇航出版社,2007:54-149. [12] 朱一锟,周家胜,石光煜.航天飞机机翼外形优化的初步设计方法[J].北京航空航天大学学报,1997,23(2):183-185. [13] 陈刚,万志明.基于遗传算法的RLV再入轨迹优化设计[J].系统工程与电子技术,2006,28(8):1240-1243. [14] 陈刚,万志明.遗传算法在轨迹优化中的应用评述[J].弹道学报,2006,18(1):1-5. [15] 吴胜亮,南英,黄国强,等. 随机风场与升阻比误差对空空导弹可攻击区的敏感度研究[J].弹道学报,2012, 24(02):25-30. Influencesofaerodynamicshapesonreentryfootprintofspacevehicle HU Hai-long, NAN Ying (School of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China) The influences of reentry flight are researched for space vehicles caused by the different aerodynamic shapes, the reentry footprint are regarded as the characteristic of the flight ability to predict the voyage. Based on the genetic algorithm for flight trajectory optimization, the optimization algorithm of the reentry footprint is proposed, and the numerical simulation results of reentry footprints are obtained for space vehicles with different lift-to-drag ratios, considering all kinds of constraint conditions. And then the obtained numerical simulation results are analysed to get the numerical relationship between the voyage and the lift-to-drag ratios, which achieves the goal of voyage prediction. And the reentry flights are also analysed to get the influences on the characteristics of reentry flight trajectories and the best aerodynamic shape for the given flight mission. reentry space vehicle; genetic algorithm; reentry footprint; lift-to-drag ratio; numerical simulation V448.2 A 1002-0853(2013)06-0545-04 2013-04-09; 2013-05-22; < class="emphasis_bold">网络出版时间 时间:2013-08-21 18:47 胡海龙(1990-),男,江西南昌人,硕士研究生,研究方向为航天器轨迹优化与控制。 (编辑:李怡)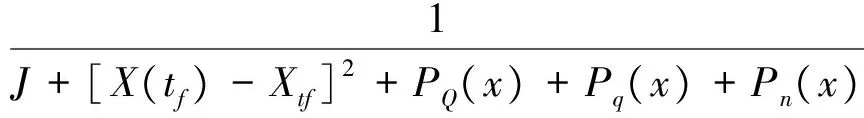
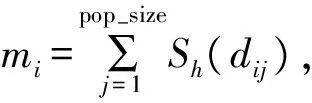
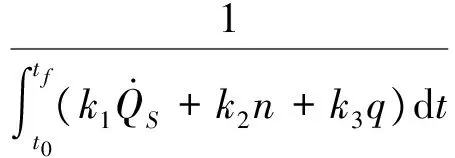
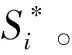
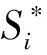
3 再入终迹圈数值仿真结果与分析
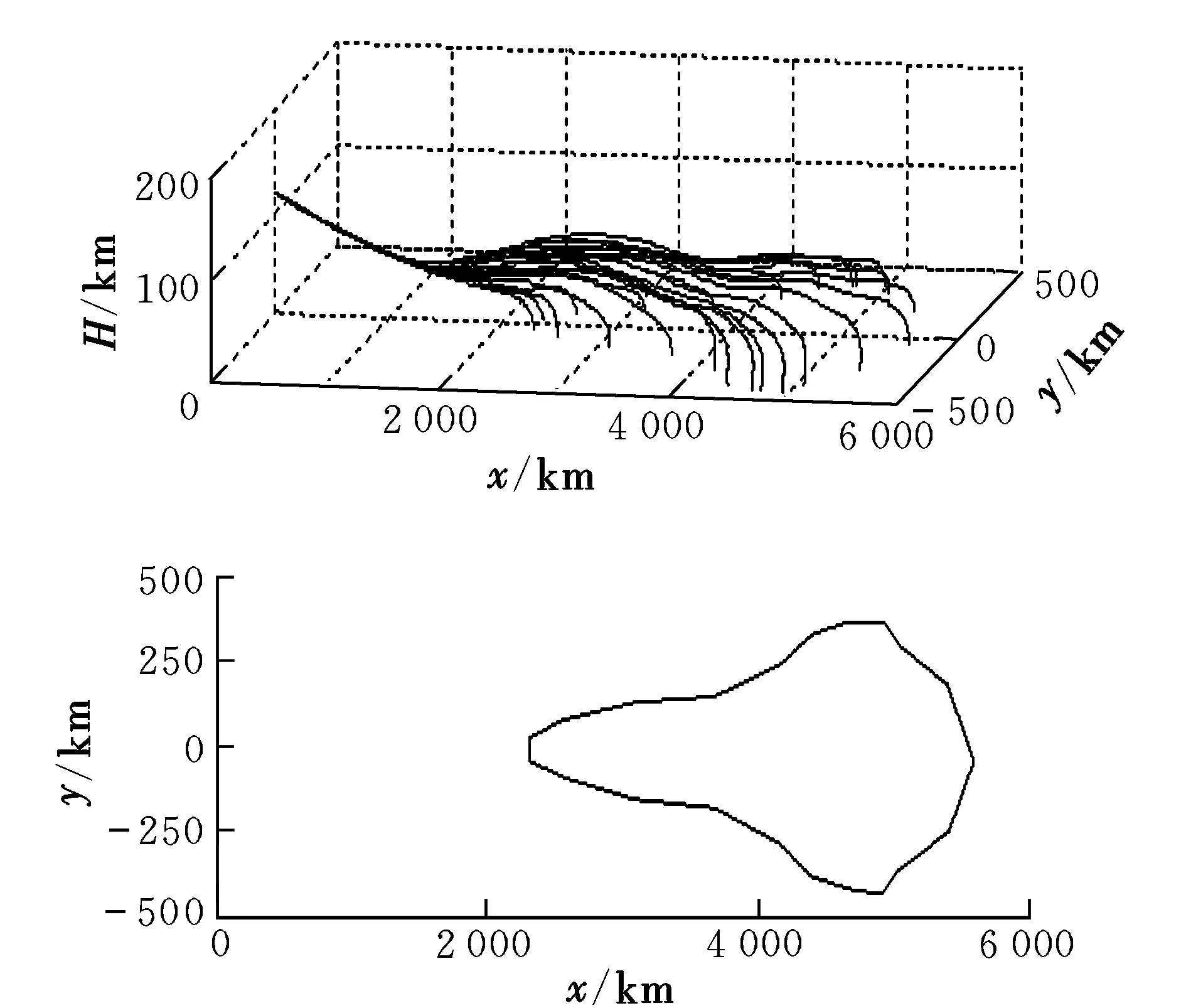
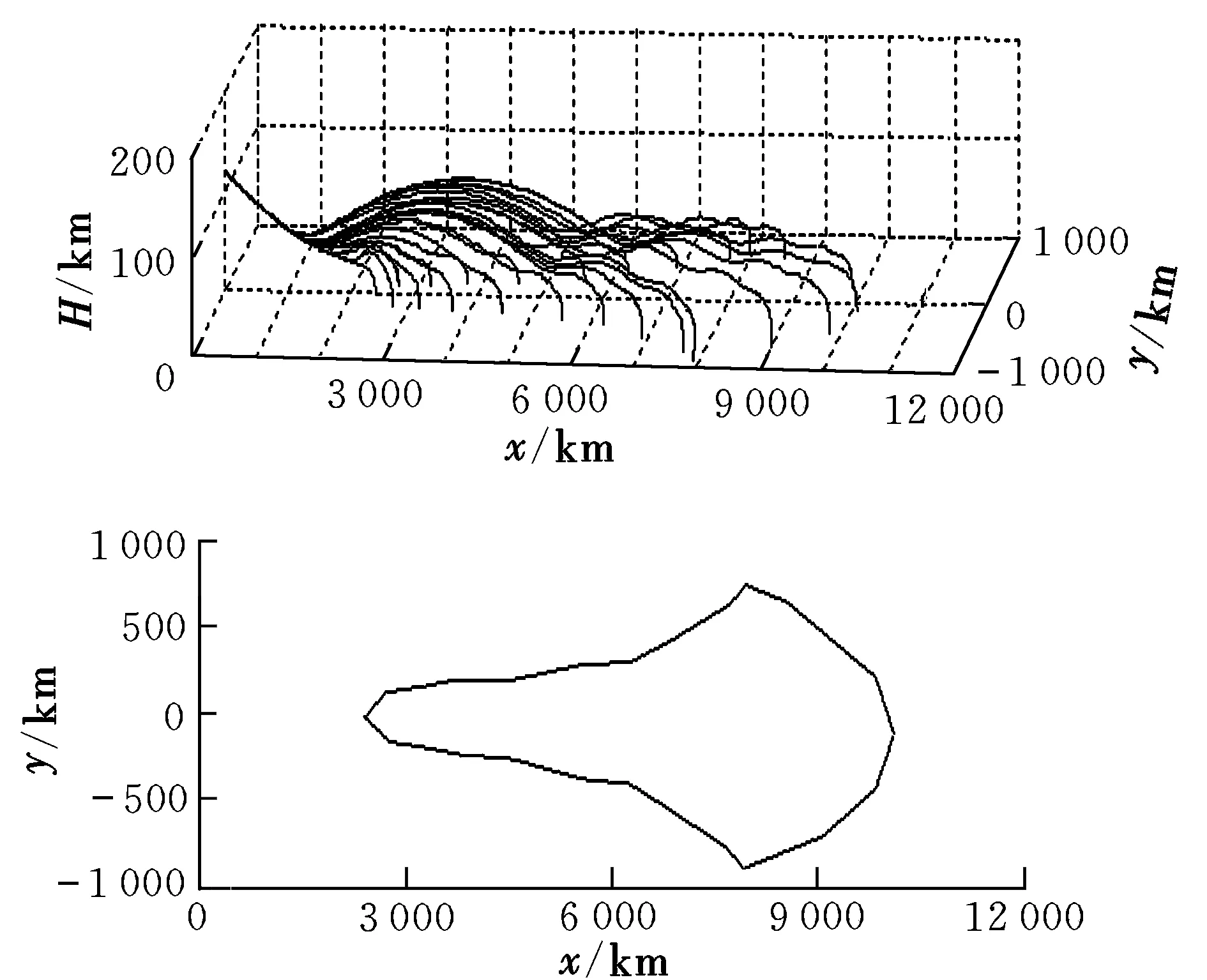
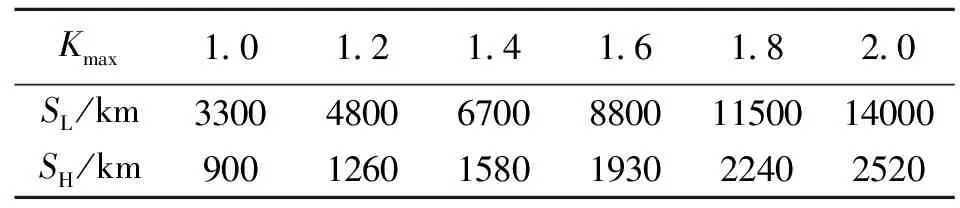
4 结论
