关于容斥原理在勒贝格积分中的应用及推广*
2013-11-02唐大钊
唐大钊,雷 桥
(重庆师范大学 数学学院,重庆401331)
黎曼将柯西只对连续函数定义的积分概念扩张成现在黎曼积分(即R积分),从而扩大了积分的应用范围.但是即使在有界函数范围内,R积分还是存在着很大的缺陷.而勒贝格积分基于可列可加的测度,从很大程度上摆脱了R积分的困境,大大扩充了可积函数的范围;而可测函数的一些基本性质,则是建立勒贝格积分的基础.容斥原理是组合计数的基本方法,
基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,受此启发,将容斥原理推广到可测函数中,就得到了一些新的结论.
1 相关性质
定义1[1]设E⊆Rq为可测集,φ(x)为E上的一个非负简单函数,即E表示有限个互不相交的可测集E1,E2,…,Ek之并,而在每个Ei上 φ(x)取非负常数值ci,即 φ(x)=),这里 χEi(x)是 Ei上的特征函数;φ(x)在E上的勒贝格积分(简称L积分),定义为x)d x=
设A⊆E为可测子集,φ(x)在A上的勒贝格积分定义为φ在A上的限制在A上的勒贝格积分,于是
定理1[2]设E∈Rq为可测集,φ(x)为E上的一个非负简单函数.设A和B是E的两个不相交的可测子集,则:
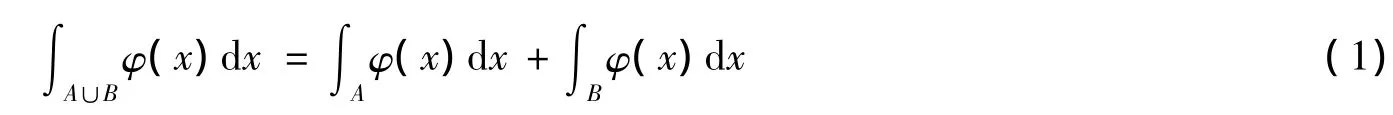
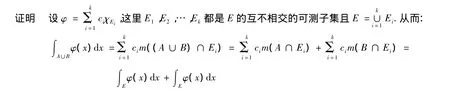
定理2[3]设S是有穷集,P1,P2,…,Pm是m个性质.S中任何一个元素x对于性质Pi(i=1,2,…,m)具有或不具有,两者必居其一.令Ai表示S中具有性质Pi的元素构成的子集.那么,S中不具有性质P1,P2,…和Pm的元素数是:
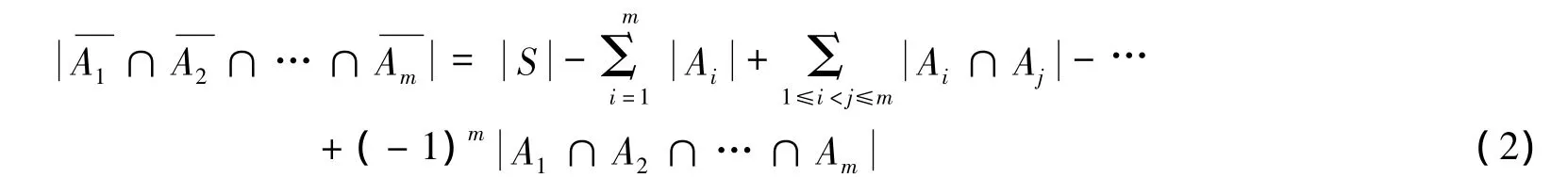
证明 等式左边是S中不具有性质P1,P2,…,Pm的元素数.将要证明,对S的任何一个元素x,如果x不具有性质P1,P2,…,Pm,则对等式右边的贡献为1;如果x至少具有其中的一条性质,则对等式右边的贡献为0.
设 x 不具有性质 P1,P2,…,Pm,所以 x∉Ai,i=1,2,…,m.令 T={1,2,…,m}.对 T 的所有2 - 组合(i,j)都有 x∉Ai∩Aj,对 T 的所有 3 - 组合(i,j,k)都有 x∉Ai∩Aj∩Ak,…,直到 x∉A1∩A2∩…∩Am.但 x∈S,所以它对等式右边的贡献是1-0+0-0+…+(-1)m0=1.

2 结论
推论1 设E∈Rq为可测集,φ(x)为E上的一个非负简单函数.设A和B是E的两个可测子集,则:
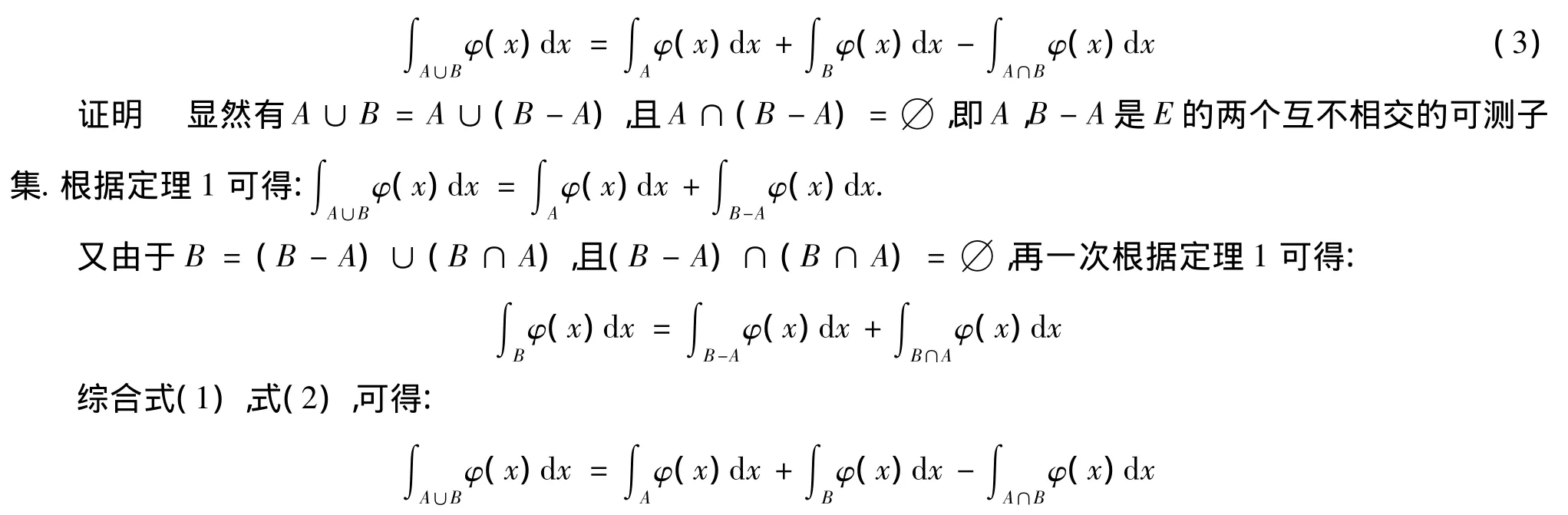
推论2 设E∈Rq为可测集,φ(x)为E上的一个非负简单函数.设A,B和C是E 3个可测子集,则有:
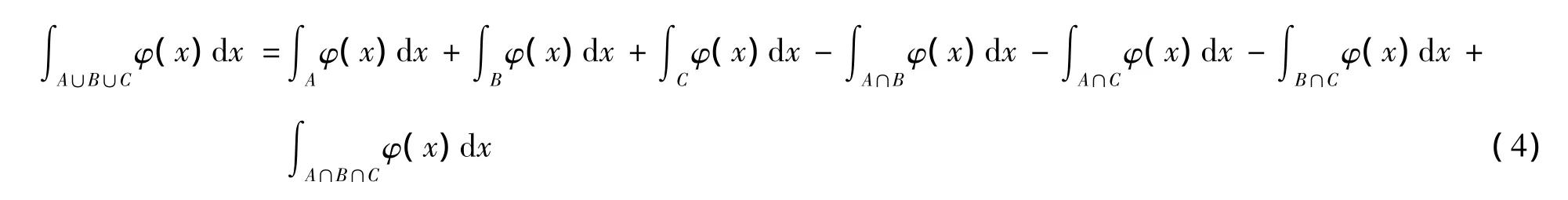
证明 由于A∪B∪C=A∪(B-A)∪(C-(A∪B)),且A,B-A,C-(A∪B)是E的3个互不相交的可测子集,因而反复应用定理1可知:

将推论中可测集合的个数推广到n个的情形,再结合定理2得出以下推论.

由非负简单函数与非负可测函数、一般可测函数的关系,可以得到如下推论.

[1]程其襄,张奠宙.实变函数与泛函分析基础[M].3版.北京:高等教育出版社,2010
[2]周民强.实变函数论[M].北京:北京大学出版社,2012
[3]屈婉玲.组合数学[M].北京:北京大学出版社,2010
