向量优化问题ε-真有效解的一个性质*
2013-11-02赵克全
彭 婕,赵克全
(重庆师范大学 数学学院,重庆400047)
众所周知,向量优化的理论与方法在经济、管理、最优决策等许多领域中具有十分重要的作用.近年来,一些学者已经开始研究向量优化问题的近似有效解的概念、性质及在向量优化中的应用.Kutateladze在文献[1]中首次引入了凸多目标优化问题的ε-有效解的概念.Loridan在文献[2]中提出了一般向量优化问题的ε-有效解的概念.文献[3]则利用经典的G-真有效解的思想提出了ε-真有效解的概念并研究了ε-真有效解的一些最优性条件.戎和马在文献[4]中基于经典的Benson-真有效解的思想提出了一类新的ε-真有效解的概念并在广义次似凸性假设下研究了带集值映射的向量优化问题的ε-真有效解的一些标量化结果和Lagrange乘子定理.戎和武在文献[5]中在广义次似凸性假设条件研究了带集值映射的向量优化问题的ε-弱有效解的一些标量化结果,Lagrange乘子定理鞍点定理和对偶定理.
受文献[3,4,6,7]的启发,在次似凸性假设下,证明了ε-真有效解集的一个性质.该性质提出了向量优化问题的ε-真有效解集为空的一个充分条件,结果是对最近一些文献中相应结果的改进与推广.
1 预备知识
考虑如下向量优化问题:

其中 S⊂Rn,f:S→Rm.令 J={1,2,…,m}.
考虑如下与问题(VP)相对应的数值优化问题:
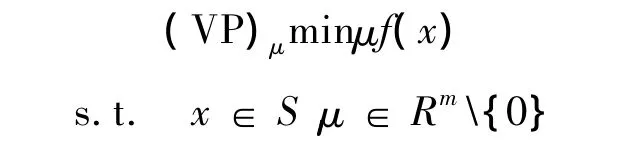
定义1[1]令ε∈.称x0∈S是(VP)的ε-有效解,如果不存在x∈S使得f(x)≤f(x0)-ε.记(VP)的ε-有效解集为ε-E(f(S),).
定义2[3]令ε∈.x0∈S是(VP)的ε-真有效解当且仅当
(i)x0是(VP)的ε-有效解.
(ii)存在M>0使得对任意的i,只要x∈S且fi(x0)>fi(x)+εi,则存在j∈J满足fj(x0)<fj(x)+εj且
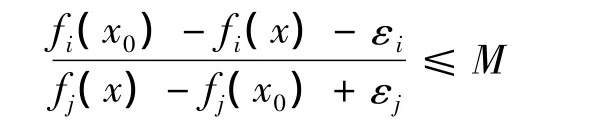
定义3[3]x0∈S 称为问题(VP)的 ε -最优解,如果 μTf(x0)≤μTf(x)+ μTε,∀ε∈S.
定义4[4]x0∈S称为问题(VP)的ε-真有效解当且仅当clcone(f(S)++ε-f(x0))∩(-)={0}.
定义5[7]f称为S上的-次似凸函数,如果f(S)+是凸集.引理1[4]若f是S的-次似凸函数,那么x0是问题(VP)的ε-真有效解当且仅当存在μ∈使得x0是问题(VP)μ的ε-最优解.
引理2[8]定义2等价于定义4.
2 ε-真有效解的性质
这部分给出ε-真有效解的一个性质.该性质提出了向量优化问题(VP)的ε-真有效解集为空的一个充分条件.
考虑与问题(VP)相对应的如下数值优化模型:

证明 由上得,因问题(VP)μ无有限最大值存在,故对任意的,存在满足下面的系统

若存在x*∈ε-PE(f(S),),由引理1和引理2可知存在μ∈=1使得x*是问题(VP)μ的ε-最优解,这样,对任意的x∈S,可得


这与(2)矛盾.
注 显然,推论减弱了文献[6]中定理3的条件.
[1]KUTATELADZE S.Convex ε-programming[J].Soviet Mathematics.Dokl,1979,20:391-393
[2]LORIDAN P.ε-solutions in vector minimization problems[J].Journal of Optimization Theory and Applications,1984,43:265-276
[3] LIU J C.ε-Properly eきcient solutions to nondiあerentiable multiobjective programming problems[J].Applied Mathematics Letters,1999,12:109-113
[4]RONG W D,MA Y.ε-Properly eきcient solutions of vector optimization problems with set-valued maps[J].OR Transactions,2000,4:21-32
[5]RONG W D,WU Y N.ε-Weak minimal solutions of vector optimization problems with set-valued maps[J].Journal of Optimization Theory and Applications,2000,106:569-579
[6]BENSON H P.Existence of eきcient solutions for vector maximization problems[J].Journal of Optimization Theory and Applications,1978,26:569-580
[7]CHEN G Y,RONG W D.Characterizations of the Benson proper eきciency for nonconvex vector optimization[J].Journal of Optimization Theory and Applications,1998,98:365-384
[8]ZHAO K Q,WAN X,PENG J.ε-Eきciency in vector optimization problems[J].Journal of Chongqing Normal University(Natural Science),2012,29(5):1-5
[9]龙莆均,皮巧丽,赵克全.关于KT一伪Ⅱ型不变凸性的一个注记[J].重庆工商大学学报:自然科学版,2012,29(1):16-18
