半连续模糊映射的性质
2013-11-02刘婷婷
刘婷婷
(重庆师范大学 数学学院,重庆401331)
1 简单介绍
上下半连续实值函数在优化理论中扮演重要的角色.此处引进了关于模糊集和模糊映射的上下半连续的概念和参考了很多文献.例如,Ramik研究了上/下半连续的模糊集的概念.基于上半连续模糊集的概念,Ramik确定了决定获得最大-最小值的条件.
在Hausdorff分离定理的基础上,Diamond和Kloeden[4]引入上下半连续模糊映射的概念.最近,Bao和Wu[1]通过在模糊数上的“模糊较大值”,引进了一种新的上下半连续模糊映射的概念.在参考文献[5]里,“模糊较大值”的线性准则在模糊数上是一种偏序关系.基于Goetschel和 Voxman[2]提出的线性准则,论文[6]延伸了从一个实值函数到模糊映射的维尔斯特拉斯定理.
2 预备知识
令Rn为n维欧式空间,一个模糊集u:Rn→I=[0,1]的支集,记为sup p(u),定义为sup p(u)={x∈Rn:u(x)>0}.
正规集:一个模糊集u:Rn→I是正规的,如果[u]1≠∅.
α -水平集:令 α∈I,一个模糊集 u:Rn→I=[0,1],记为[u]α,α -水平集定义为
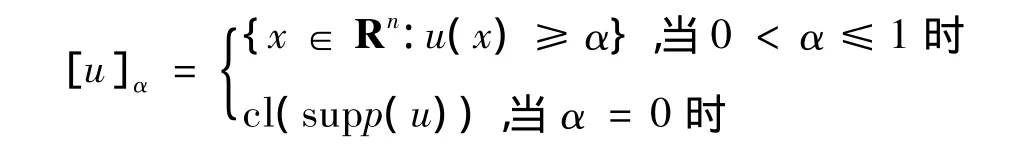
其中cl(sup p(u))定义为支集的闭包.所有的模糊数记为F,所考虑的是F映射从Rn的子集S映到F,称这样的映射为模糊映射.显然能证到一个模糊映射集u:R1→I当且仅当
(i)对于每个 α∈[0,1],[u]α为一个有界闭区间.

这样,可定义模糊数u的参数形式{(a(α),b(α),α)0≤α≤1},其中 a(α)和 b(α)分别记为[u]α的左和右端点.
定义1[2]设 m,n为两个模糊数,参数表达式分别为{(a(α),b(α)≤α≤1}和{(c(α),d(α),≤α≤1},特别地,m大于等于n(记作m≥-n).
满足

紧接着,令 S为非空 Rn的子集,对于任意 x∈Rn和 δ>0,令Bδ(x)={y∈Rn:‖y-x‖ < δ}.
定义3[8]一个实值函数f:S→R1是
(1)在 x0∈S上上半连续,如果∀ε >0,存在一个 δ=δ(x0,ε)>0,使得 f(x)<f(x0)+ε,其中 x∈S∩Bδ(x0),并且f在S上是上半连续的,如果它在S的每个点都是上半连续的.
(2)在 x0∈S上下半连续,如果∀ε >0,存在一个 δ=δ(x0,ε)>0,使得 f(x)>f(x0)-ε,其中 x∈S∩Bδ(x0),并且f在S上是下半连续的,如果它在S的每个点都是下半连续的.
引理1[9]令X是一个非空有界闭的Rn的子集,一个实值函数f:Rn→R1在X上是上(下)半连续,则在X上可获得它的最大(小)值.

(2)因为f(x)在任何内闭区间上无上界,所以对Bδ1(x1),∃x2∈Bδ1(x1),使得f(x2)>2,而由f(x)的下半连续,知∃δ>0(令,使得∀x∈B(x)⊂B(x),有 f(x)>2.2δ22δ11
(3)由此继续下去,可得到一串闭区间Bδ1(x1)⊃B1δ2(x2)⊃…⊃B2δn(xn)…,区间长→ +∞时),且对每个区间 Bδn,恒有 f(x)>n.
(4)根据区间套定理,∃ξ∈δn(n=1,2,…),所以 f(ξ)=+∞.矛盾
注2 定理2是对参考文献[10]由一维到n维空间的推广.
3 上下半连续模糊映射
定义4[1]令F:S→F的一个模糊映射的参数形式为
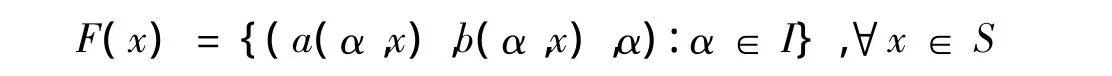
(1)F:S→F在x0∈S上是上半连续的,如果a(α,x)和b(α,x),对于所有的α∈I,在x0处都上半连续;F:S→F是上半连续的,如果它在S的每个点都上半连续.
(2)F:S→F在x0∈S上是下半连续的,如果a(α,x)和b(α,x),对于所有的α∈I,在x0处都下半连续;F:S→F是下半连续的,如果它在S的每个点都下半连续.
4 主要结论
引理2[9]如果F:Rn→F是上半连续,则TF:Rn→R1也是上半连续.
引理3[9]如果F:Rn→F是下半连续,则TF:Rn→R1也是下半连续.
引理4[9]令X为一个非空的Rn的有界闭子集,如果F:X→F是一个上半连续函数,则F在X上达到最大值.
注3 令X为一个非空的Rn的有界闭子集,如果F:X→F是一个下半连续函数,则F在X上达到最小值(证明方法相同).把条件有界闭改为紧集也成立.
证明 若F为上半连续映射,由引理4知,F有上界,下证其有下界.
因为F上半连续,则TF在X上为上半连续函数,由定理2得存在闭区间X,使得TF有下界.因为X为闭的,则TF能达到下确界.
设在x**∈X达到下确界,由式(3)得,x**为F的下确界,则F在X中有界.n
注4 定理2可改为(ai,bi)为一开区间(ai,bi)∈R,存在 X 为(ai,bi)中的闭集,如果 F:ai,bi)→F上的下半连续,则F在X中保持有界.
[1]BAO Y E,WU CX.Convexity and semicontinuity of fuzzy mappings[J].Comput Math Appl,2006(51):1809-1816
[2]GOETSCHEL R,VOXMAN W.Elementary fuzzy calculus[J].Fuzzy Sets and Systems,1986(18):31-34
[3]RAMIK J,VLACH M.Pareto-optimality of compromise decision[J].Fuzzy Sets and Systems,2002(129):119-127
[4]YANG X.A property on convex fuzzy sets[J].Fuzzy Sets and Systems,2002(126):269-271
[5]YANG X.A note on convex fuzzy sets[J].Fuzzy Sets and Systems,1993(53):117-118
[6]SYAU Y R,LEE E S.Fuzzy Weierstrass theorem and convex fuzzy mappings[J].Comput Math Appl,2006(51):1741-1750
[7]YANG X.Some properties of convex fuzzy sets[J].Fuzzy Sets and Systems,1995(72):129-132
[8]AUBIN JP.Applied Abstract Analysis[M].Wiley-Interscience,New York,1977
[9]SYAU Y R.A class of semicontinuous fuzzy mappings[J].Applied Mathematics Letters,2008(21):824-827
[10]LONG PJ.上半连续和下半连续[DB/OL].http:∥wenku.baidu.com/view/6da61473f242336c1eb95e8b.html,2010
