一类三阶具多偏差变元微分方程的周期解*

施吕蓉，周宗福，高 伟

(1.芜湖职业技术学院，安徽 芜湖241003;2.安徽大学数学科学学院，安徽合肥230000)

1 基础知识

微分方程的周期解由于应用广泛而被人们广泛关注，近年来，一阶和二阶微分方程周期解的存在性研究已有很多结果.在三阶微分方程的研究中，文献［1］［2］研究了三阶常微分方程

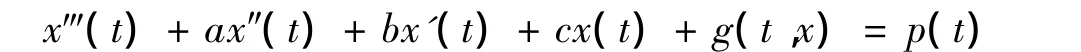
文献［3］讨论了三阶具偏差变元微分方程

的2π－周期解的存在性.其中f(x)∈C(R)，τ(t)，p(t)均为2π－周期连续函数.这里，将研究方程

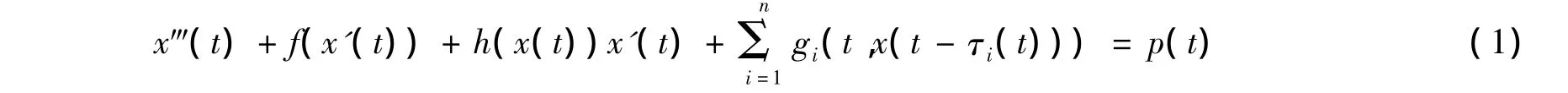
的 T－周期解的存在性，其中 f(x)，gi(t，x)(i=1，2，…，n)在 R 上连续，g关于 t为 T周期的 ，p(t)及 τ1(t)，τ2(t)，…，τn(t)都是以T为周期的连续函数.

引入下列记号:

易见算子方程Lx=Nx与式(1)等价.其辅助方程为

利用辅助方程(2)，容易证得以下结果:

引理1 若x(t)是式(2)的一个T－周期解，当(H1)(H3)或(H2)(H4)任一组条件成立时，

2 主要结果

定理1 若(H1)(H3)成立，并且条件(H5)(H7)或者(H6)(H7)成立，则当2(n－1)时，方程(1)至少存在一个T－周期解.

证明 记方程(2)的所有T－周期解组成的集合

∀x∈Ω0，对方程(2)两端从0到T积分，有

由引理1并结合(H5)(H7)可知

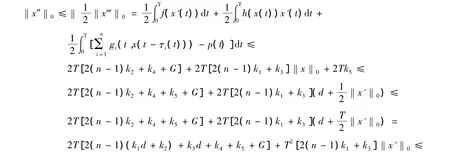
因而存在与λ无关的常数K＞K0+K1+K2，使得‖x‖＜K.

作变换 F:(Ω∩Ker L)×［0，1］→Ω∩Ker L，定义

故F(x，u)为同伦映射，取J为恒同映射，则

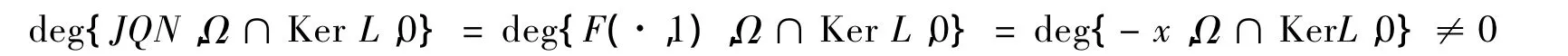
根据文献［4］的结论，方程(1)至少存在一个T－周期解.同理可得(H1)(H3)(H6)(H7)成立时，定理1依然成立.证毕.

类似于定理1的证法，可以证明下列结论成立.

定理2 若(H2)(H4)成立，并且条件(H5)(H7)或者(H6)(H7)成立，则当2(n－1时，方程(1)至少存在一个T－周期解.

［1］KIGURADZE I T，PUZA B.On periodic solutions of system of differential equations with deviating arguments［J］.Nonlinear Anal TMA，2000，42:229-242

［2］MARTINSR F.The existence of periodic solutions for second order differential equation with singularities and the strong force condition［J］.Math Anal Appl，2006，317:1-13

［3］汪娜，鲁世平.一类三阶具偏差变元微分方程的周期解［J］.安徽师范大学学报，2006，29(1):17-22

［4］GAINESR E，MAWHIN JK.Coincidence Degree and Nonlinear Differential Equation［A］.Lecture Notes in math［C］.Berlin:Springer-Verlag，1977