基于OpenSees的空心矩形梁滞回曲线分析
2013-11-02黄福伟
朱 永,黄福伟
(1.重庆交通大学土木建筑学院,重庆400074;2.重庆交通科研设计院有限公司,重庆400067)
横系梁作为连接桥塔的构件,其抗震性能的好坏将决定桥塔的抗震性能好坏。目前,国内外对于横系梁的抗震研究较少,基于其重要的作用,因此有理由相信横系梁的研究将会成为今后桥梁界研究的一大重点。目前桥塔的横系梁大多为预应力混凝土材料,在地震作用下,桥梁的延性可以消除部分地震力,同时避免桥梁的整体破坏,而预应力结构的延性比较差,当前条件下往往被忽视,这不利于分析桥梁的抗震能力,因此深入研究预应力混凝土构件及结构的受力与变形性能有着重要的工程意义。同时对预应力混凝土构件进行弹塑性分析有助于了解构件的抗震性能。借助非线性有限元模型可实现预应力结构的弹塑性模拟。OpenSees的全称是Open System for Earthquake Engineering Simulation(地震工程模拟的开放体系)。它是由美国国家自然科学基金(NSF)资助、西部大学联盟“太平洋地震工程研究中心”(Pacific Earthquake Engineering Research Center,简称PEER)主导、加州大学伯克利分校为主研发而成的、用于结构和岩土方面地震反应模拟的一个较为全面且不断发展的开放的程序软件体系。
1 预应力混凝土结构有限元分析方法
目前分析软件常用的数学模型是利用实体单元模拟钢筋混凝土,用桁架(Truss)单元模拟预应力筋。实体有限元模型由于自由度数多,因此计算量相对较大,虽然模型可应用于构件的性能分析但是不适用于预应力结构的整体分析。纤维模型由于自由度数少,适用于整体结构分析。纤维单元模拟预应力混凝土构件的关键在于处理好钢筋混凝土与预应力筋的变形协调关系。对于中空矩形预应力混凝土横梁,采用纤维单元模拟钢筋混凝土,采用桁架单元模拟预应力筋,两者之间采用刚臂连接以反映两者之间变形协调关系。本文利用开源有限元程序OpenSees对预应力横梁进行分析。
2 模型及材料本构关系
(1)纤维梁柱单元模型。一般地,纤维单元模型中的基本假定要有构件变形满足平截面假定,在变过程中横截面始终保持为平面且垂直于其轴线;钢筋与混凝土充分粘结,无相对滑移、变形协调,且不考虑剪切变形;扭转作用为线弹性且与弯矩、轴力不耦联。利用OpenSees中基于柔度法的纤维单元模型对预应力钢筋混凝土横梁的非线性滞回性能进行分析,钢筋混凝土构件截面可划分为若干个非约束混凝土纤维,约束混凝土纤维,钢筋纤维及预应力钢筋纤维,用户可以分别定义每根纤维的编号,位置,截面面积和材料属性。程序自动根据平截面假定得到每根纤维的应变,并通过迭代计算确保截面受力平衡。
(2)混凝土材料模型。混凝土采用Concrete02材料模型,模型是Scott等人修正后的Kent-Park模型(1971、1982)。模型通过改变混凝土受压骨架曲线的峰值应力、峰值应变以及软化段斜率来考虑横向箍筋的约束影响,且可以考虑混凝土的剩余强度;而混凝土受拉时的上升段和下降段均为直线,可考虑混凝土的初始开裂;卸载的应力-应变关系采用Karsan-Jirsa(1969)[140]卸载规则确定。Concrete02混凝土模型是在简化与精确之间的一种较好的平衡,对钢筋混凝土桥墩非线性分析有良好的精度。
(3)钢筋材料模型。钢筋采用Steel02,材料模型的应力应变关系采用最初由Menegotto和Pinto(1973)[141]所建议后经Taucer(1991)[142]等人修正以考虑等向应变硬化影响的本构模型,骨架曲线为双线性模型。
(4)预应力筋材料模型。预应力筋采用桁架(Truss)单元来模拟,预应力通过Steel02 Material定义初始应力来实现(有些材料也可以通过初始应变来实现)。二次刚度根据极限强度和屈服强度以及对应的应变取值。
3 横梁滞回性能数值分析
在此以长2.5 m,中空矩形截面(外高 0.7 m,外宽 0.65 m,内高 0.5 m,内宽 0.45 m)横梁为例进行计算,有限元模拟采用纤维梁元模型,基于单元材料的应力-应变本构关系,截面可以分为约束混凝土纤维单元(外部,内部共8个小矩形截面)、未约束混凝土单元(共4个小矩形截面)、钢筋纤维单元,预应力钢筋采用杆单元模拟,用初始应力模拟预张力,左侧预应力筋锚固端与横梁左侧用刚臂连接,右侧预应力筋与横梁右侧用刚臂连接。材料特性如表1所示,计算模型如图1、图2所示,计算工况如表2所示。

表1 材料特性 MPa
考虑普通钢筋配筋率、预应力钢筋配筋率、预应力大小的改变对侧向力-位移曲线的影响。计算工况编号C1C-1表示无预应力钢筋的纯普通钢筋混凝土横梁模型,C1C-2表示无普通钢筋加入的纯预应力钢筋混凝土横梁模型,C1C-3表示既有普通钢筋又有预应力钢筋的预应力钢筋混凝土横梁模型。A表示普通钢筋配筋率有变化,B表示预应力钢筋配筋率有变化,C表示预应力大小发生变化,D表示总截面配筋率相同情况下,普通钢筋配筋率和预应力钢筋配筋率大小都发生变化。
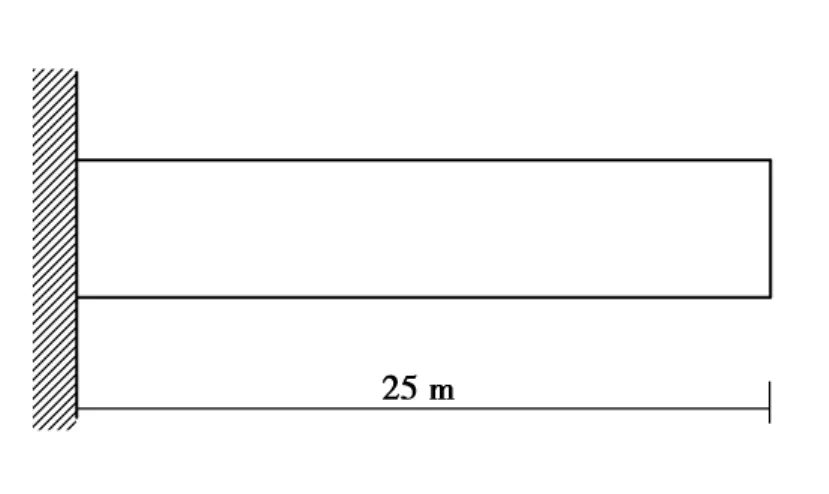
图1 模型立面图
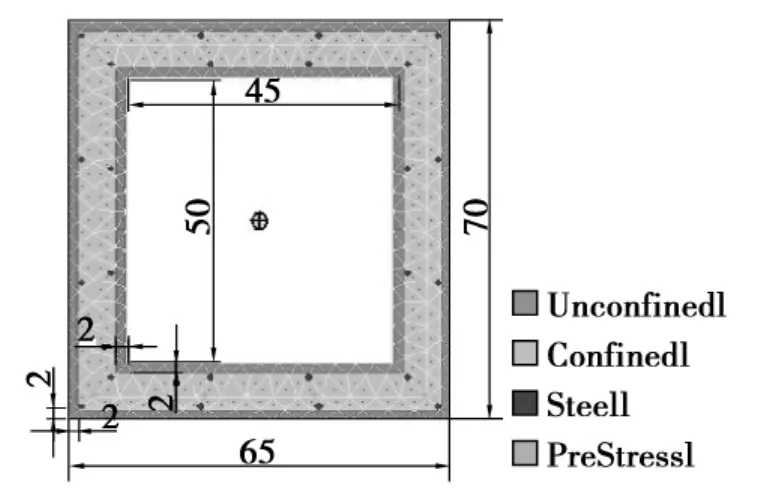
图2 模型截面
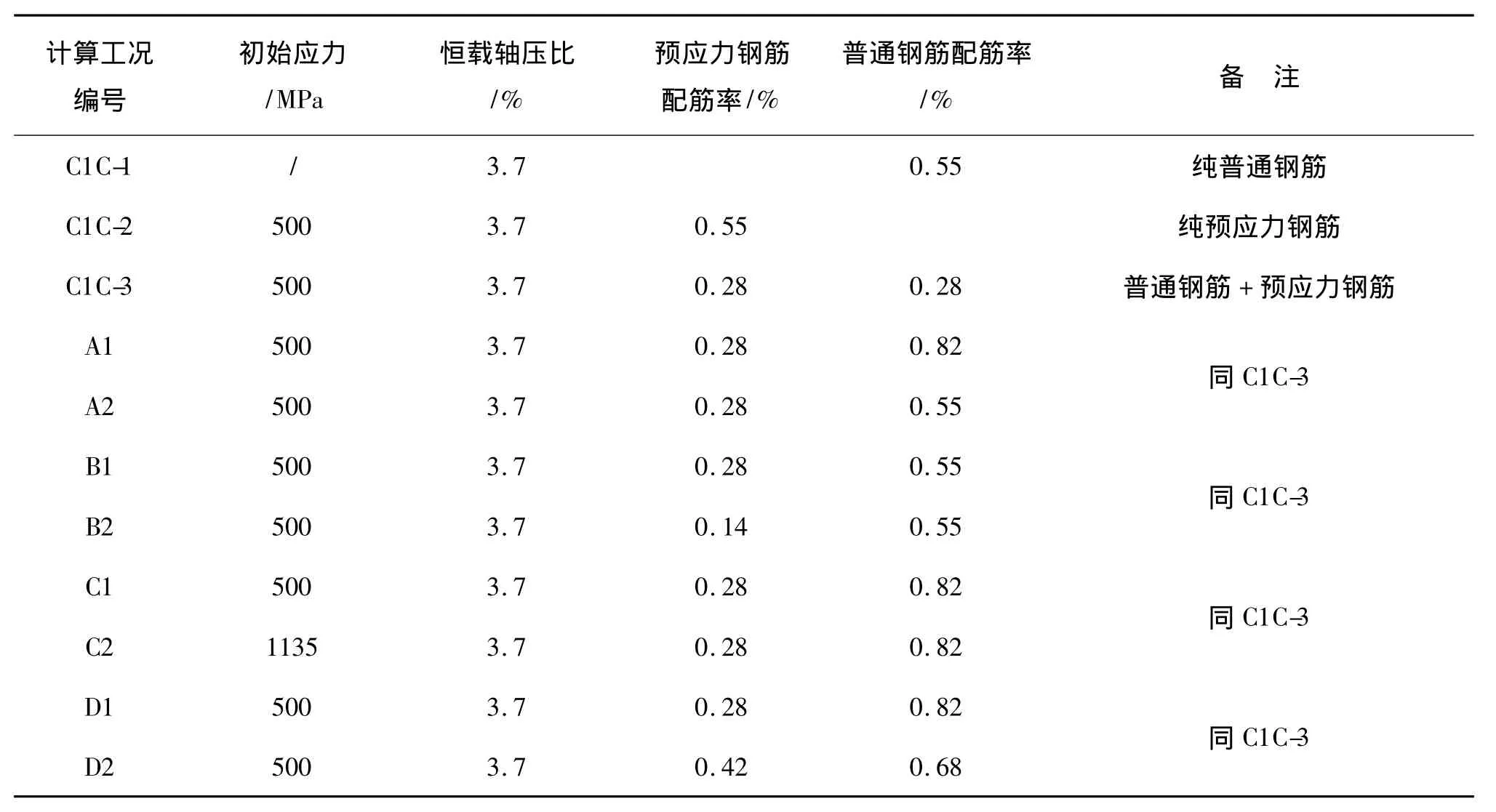
表2 计算工况
图3表示C1C-1(只配普通钢筋)、C1C-2(只配预应力钢筋)、C1C-3(兼有普通钢筋和预应力钢筋)三种情况的侧向力-位移曲线。只配预应力筋时,滞回环面积较小,卸载刚度小,残余位移几乎为零;同时有预应力筋和耗能钢筋时,卸载刚度增大,滞回环较饱满,残余位移仍然较小;只配置耗能钢筋时,卸载刚度较大,几乎没有刚度退化,滞回环最饱满,残余位移最大(0.08)。
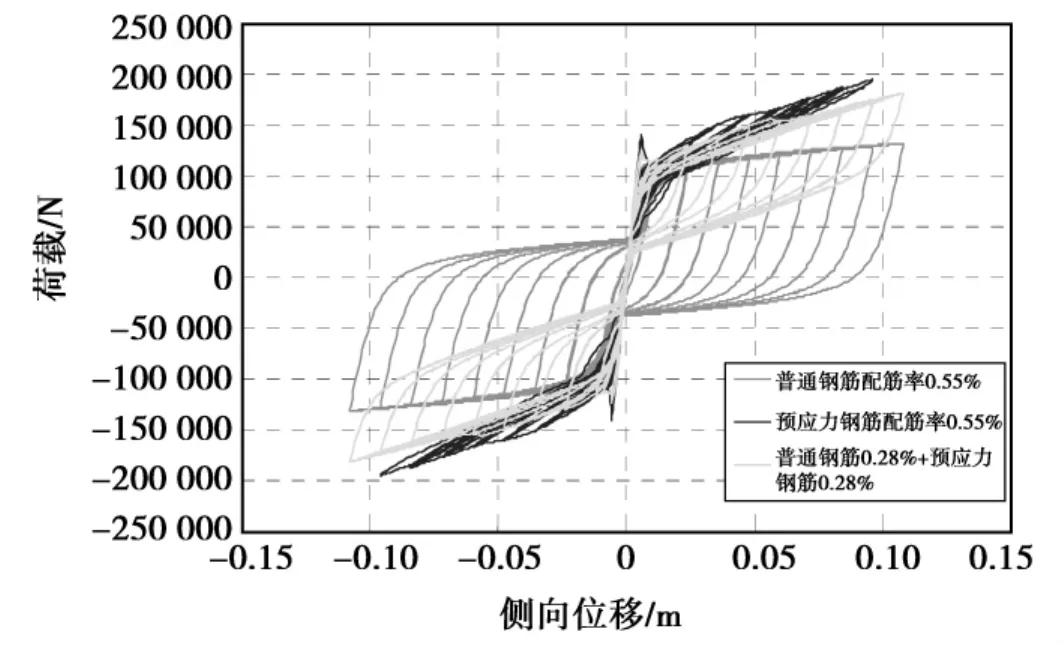
图3 3种情况下的力-位移滞回曲线
3.1 普通钢筋配筋率的影响
图4 给出了普通钢筋不同配筋率对预应力钢筋混凝土滞回曲线的影响,(a)为力-位移滞回曲线,(b)为相应的骨架曲线。其中钢筋采用直径10 mm,预应力钢筋采用直径10 mm(工况参数见表2中A1、A2、),由分析结果可以看出:随着普通钢筋配筋率增大,侧向承载力和屈服力提高,滞回曲线饱满,包络面积增大,缓解了捏拢现象,耗能能力加强。能量耗散对普通钢筋配筋率比较敏感,随着配筋率的增大,能量耗散显著增大,延性增强,对抗震有利。
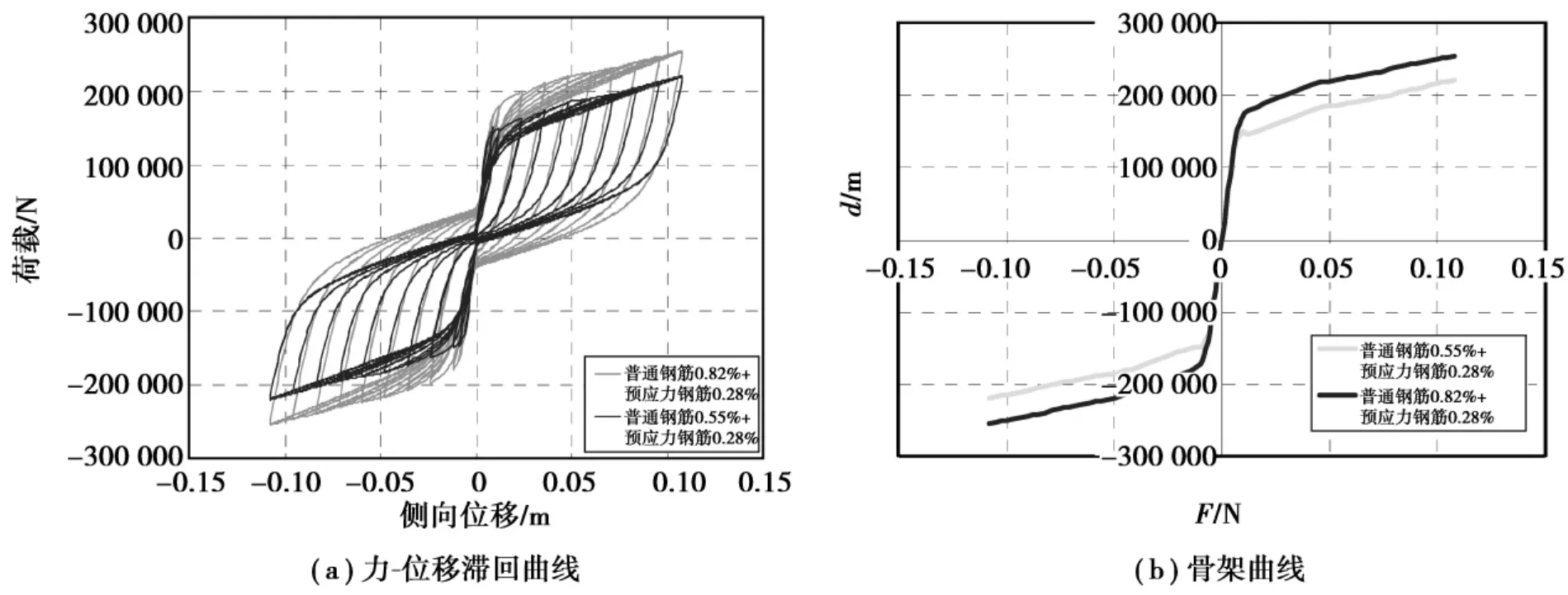
图4 普通钢筋配筋率对预应力钢筋混凝土构件滞回曲线的影响
3.2 预应力钢筋配筋率的影响
表2中计算工况编号A1、A2预应力钢筋配筋率分别为0.28%、0.14%。图5为预应力筋配筋率对侧向力-位移曲线的影响,(a)为力-位移滞回曲线,(b)为相应的骨架曲线。随着预应力筋配筋率的增加,侧向承载力明显增大,残余位移减小,包络的滞回环面积几乎不变,说明预应力筋配筋率的增加不会明显改变构件的延性。
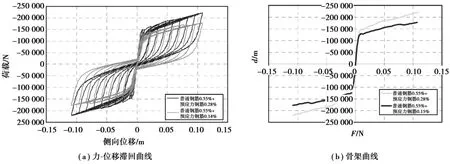
图5 预应力筋配筋率对预应力钢筋混凝土构件滞回曲线的影响
3.3 预应力度的影响
在OpenSees中预应力度可以通过改变材料的初始应力来实现,初始应力分别采用500 MPa、1 135 MPa,其他参数不变,计算模型参数对应表2中C1、C2,计算结果如图6所示,其中图5(a)表示预应力度对力-位移滞回曲线的影响,图5(b)为相应的骨架曲线,随着预应力度的提高,屈服强度提高,极限强度提高。
由分析结果可以看出,随着预应力度的增加,侧向承载力增大,滞回环包络的面积几乎不变,耗能能力近乎相同。
3.4 总配筋率相同情况普通钢筋和预应力钢筋对滞回曲线的影响
计算模型参数对应表2中D1、D2,图7给出了在截面总配筋率相同的情况下,普通钢筋与预应力钢筋配筋率不同对滞回性能的影响,(a)为力-位移滞回曲线,(b)为相应的骨架曲线。总配筋率为1.1%,预应力配筋率分别为0.28%、0.42%,普通钢筋配筋率分别为0.82%、0.68%,由分析结果可以看出随着普通钢筋配筋率提高(预应力钢筋配筋率下降),侧向承载力有所下降,残余位移有所增加,滞回环包络的面积增大,耗能能力加强。
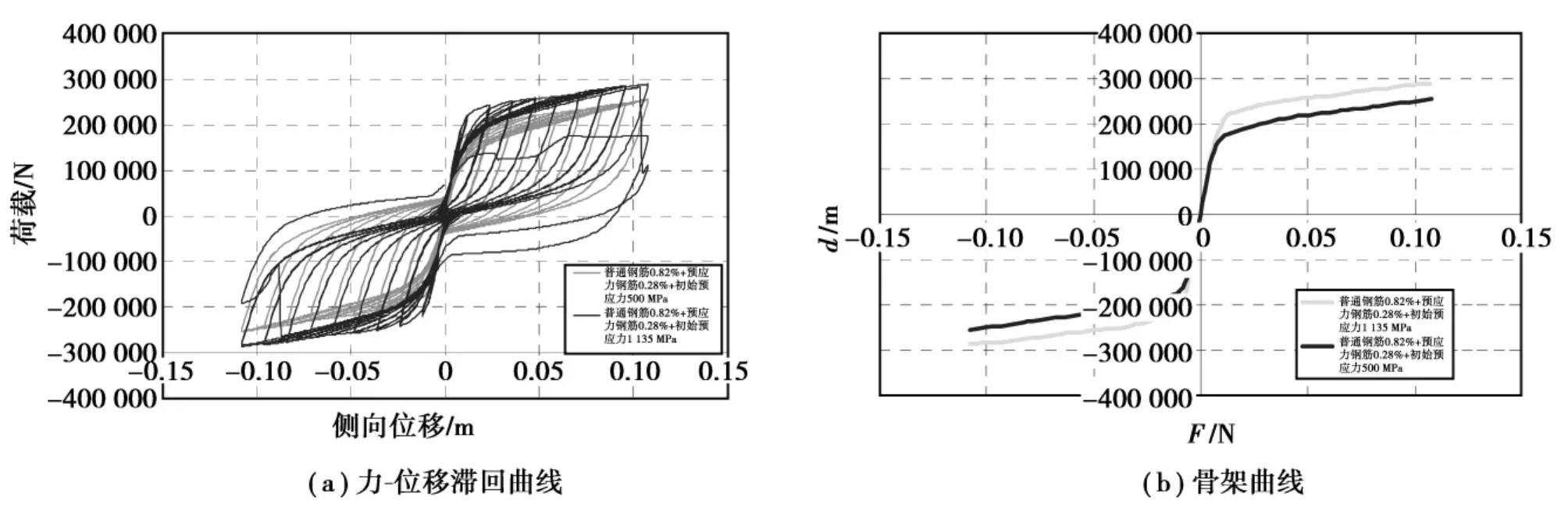
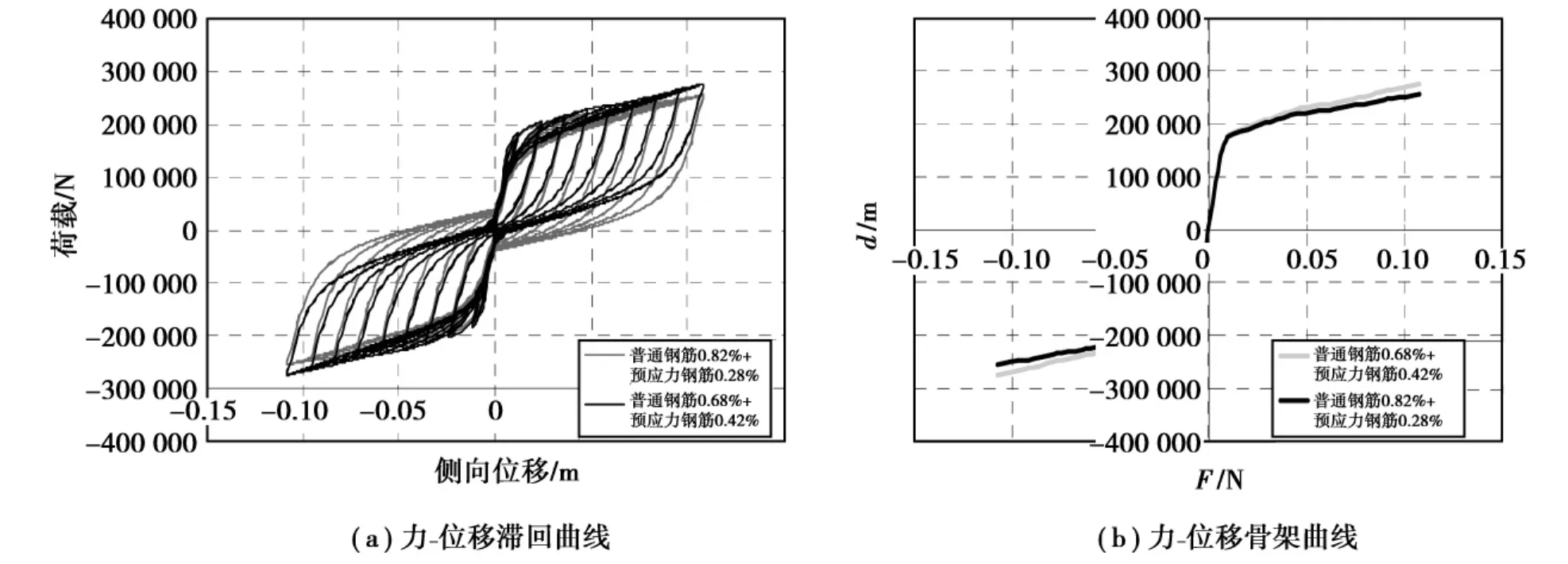
图7 截面总配筋率相同情况下,普通钢筋和预应力钢筋配筋率对截面滞回曲线的影响
4 结论与有限元模型验证
4.1 结论分析
随着普通钢筋配筋率的增加,横梁承载力有所提高,屈服强度有所提高,滞回曲线饱满,包络面积增大,耗能能力加强,延性提高,对抗震有利。随着预应力筋配筋率的提高,横梁承载力显著增大,耗能能力几乎不发生改变。随着预应力度的增大,水平承载力提高,耗能能力几乎不变。在截面配筋率相同情况下,减少普通钢筋配筋率或提高预应力钢筋配筋率可以适当提高截面的承载力,但会降低截面的耗能能力,降低结构的延性,对抗震不利。
4.2 有限元模型验证
为了验证纤维模型的正确性,分别利用纤维横梁模型和UCFiber计算了横梁关键截面处的弯矩-曲率关系,如图8所示。UCFiber计算时混凝土采用Mander建议的约束和无约束混凝土模型,普通钢筋和预应力筋采用Menegotto-Pinto模型。塑性铰长度Lp表示为Lp=0.08L+0.022fyedbl≥0.044 fyedbl,其中L是关键截面到反弯点的距离,f是纵筋屈服强度,d为纵筋直径。在塑性铰区域,墩柱曲率φ可以表示为其中yeblεc是塑性铰区域混凝土受压边缘的压应变,c为截面受压区高度。
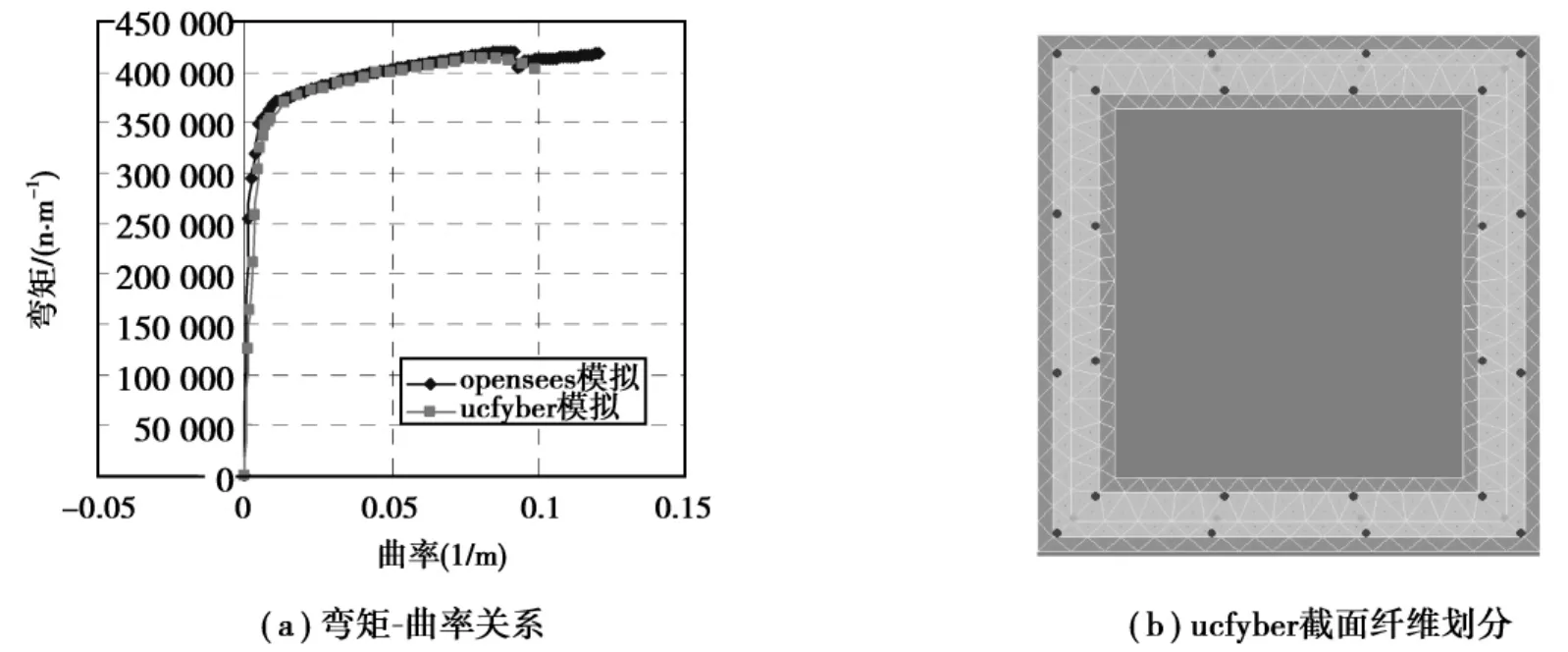
图8 弯矩曲率计算结果比较
[1]江见鲸,陆新征,混凝土结构有限元分析[M].北京:清华大学出版社,2005
[2]汪训流,叶列平.往复荷载下预应力混凝土结构的数值模拟.工程抗震与加固改造.2006,28(6):100-103
[3]王志强,葛继平,魏红一.东海大桥预应力混凝土桥墩抗震性能分析[J].同济大学学报:自然科学版,2008,36(11):1462-1466
[4]布占宇,唐光武.无黏结预应力带耗能钢筋预制节段拼装桥墩抗震性能研究[J].中国铁道科学,2011,32(3):33-40
[5]刘贤明,赵侃,谢恺.一种基于FPGA的VART IP核设计[J].四川兵工学报,2011(3):64-66
