超静定问题教学探究

殷 春 英

(衡水学院 电子信息工程学院，河北 衡水 053000)

超静定结构是实际工程中经常用到的结构，它具有良好的力学性能，可以有效地提高结构的刚度和强度，满足多种工艺要求．但由于其结构复杂，应用不当就会产生很多问题，使得学生在处理超静定问题时感到困惑，在此对超静定问题进行归纳和探究，以便学生更好地求解超静定问题，并将其应用到实际工程当中去．

1 什么是超静定问题

与超静定问题对应的是静定问题，静定问题是：对研究对象进行受力分析、列方程时，未知力个数等于独立平衡方程的数目，从数学的角度看，所有的未知量都可以求出来，此时的结构叫静定结构．超静定问题[1]是：为了提高结构的强度和刚度，有意增加约束，使得在对研究对象进行平衡分析时其未知力个数多于独立平衡方程的数目，造成不能直接把未知量求出，我们把这种结构叫超静定结构，对于超静定结构需要进一步分析，增加方程的个数，使得未知数的个数等于方程的个数，才能把所有的未知量求出来．

超静定结构就是在静定结构的基础上增加了约束，使各构件或构件各部分的变形之间互相牵制，因而具有一些与静定结构不同的特性．

2 加强对超静定问题的探究

2.1 超静定结构的分类

超静定结构按内外力可分为3 类，一是仅在结构外部存在多余约束，即支反力是超静定的，可称为外力超静定系统；第二类是仅在结构内部存在多余约束，即内力是超静定的，可称为内力超静定系统；第三类是在结构外部和内部均存在多余约束，即外力和内力是超静定的，可称为混合超静定系统．

超静定结构按未知力个数分，可分为一次超静定结构、二次超静定结构和多次超静定结构．

2.2 影响超静定结构的因素

2.2.1 刚度对超静定问题的影响

荷载作用下，超静定结构的内力除与荷载有关外，还与各杆的相对刚度有关，相对刚度越大的杆，其内力也越大．当结构存在装配误差时或温度变化时，结构就会产生相应的装配应力与温度应力，这些应力可能使结构损坏．如果在设计制作超静定结构时考虑不到这些特性，那工程将存在潜在的危险．因此需要深入研究这些特性，减少其特性对结构的不良影响，还可以合理地利用其特性，将其变成有利条件．

2.2.2 约束设计对超静定问题的影响

超静定结构有较强的防护能力．由于超静定结构存在多余约束，某些杆件被破坏后，它仍能维持几何不变性；而静定结构在任一约束被破坏后，整体结构将会变形或损坏，从而失去承载能力．因此，超静定结构常应用于抗震防灾、国防建设等方面，它与静定结构相比具有较强的防护能力，安全性能较高．

超静定结构的内力和变形分布比较均匀．静定结构由于没有多余约束，一般内力分布范围小，峰值大；刚度小、变形大．而超静定结构由于存在多余约束，与静定结构相比，其内力分布范围大，峰值小；且刚度大、变形小．因此超静定结构的整体性好，在局部荷载作用下可以减小局部的内力幅值和位移幅值，使结构的强度、刚度、稳定性都有所提高．

2.2.3 温度变化及加工误差对超静定问题的影响

温度的变化将会在超静定结构的构件中引起“温度应力”．在实际工程中，杆件遇到温度的变化，其尺寸将有微小变化．由于杆件受到互相制约而不能自由变形．对于两端固定杆件，当温度升高△T 时，在杆内引起温度应力为：

式中，E 为材料的弹性模量，而1α 则为材料的膨胀系数．加工构件时，尺寸上的一些微小误差是难以避免的．对于超静定结构，加工误差却往往要引起内力，这种内力称为装配应力，这与温度应力的形成是非常相似的．

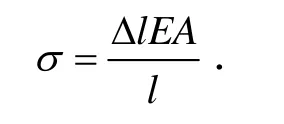
由上述原因引起的自内力一般与杆件的刚度成正比，故不应盲目增大杆件截面尺寸，以期增强杆件抵抗能力．在设计制作超静定结构时一定要考虑到自应力对结构的影响，并且可以使用预应力结构，主动利用自内力调节超静定结构内力．

3 超静定问题的解题思路

3.1 选择合适的静定基

解除超静定结构的某些多余约束后得到的静定结构为原结构的静定基本结构，简称静定基．

如图1 去掉动铰链的支撑，用一反约束力代替，这就形成了静定基．然后再根据静定基，寻找补充方程，就可求出反作用力，从而使超静定问题得到解决．结构中的静定基并不唯一，求解时，可以根据结构的具体特点选择合适的静定基．

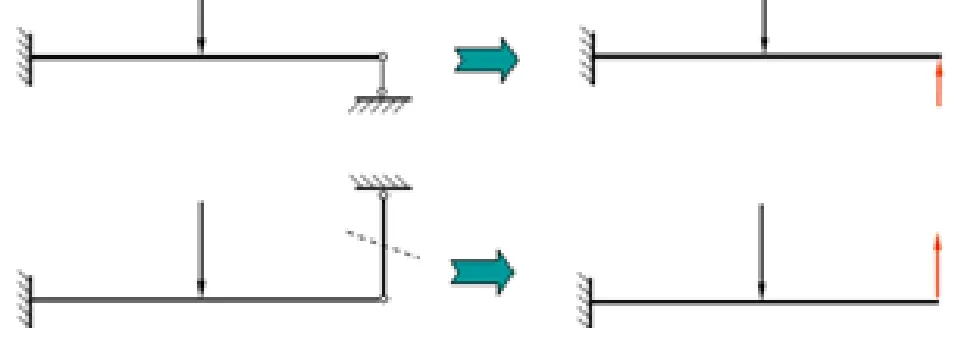
图1 静定基

3.2 补充方程

前面已提到仅用平衡条件不能解出超静定结构的全部未知力，因此我们就要寻找补充方程．补充方程的求解方法大致分4 种：

3.2.1 位移比较法列变形协调方程

虽然结构在力的作用下发生了变形，但有一些简单的构件变形后仍能找到保持某种协调一致的几何关系，位移比较法就是在多余约束处寻找这种几何关系，就得到了补充方程．前面已提到，超静定结构的求解与材料的刚度有关系，所以位移比较法还需通过力和变形之间的关系，利用胡克定律建立物理方程．这样将所列出的平衡方程，变形协调方程和物理方程联立求解[2]，便可求出全部未知力，从而使超静定结构问题得以解决．

3.2.2 用莫尔积分法列变形协调方程

莫尔积分法是指利用积分方法寻找绕度与弯矩之间的关系，由莫尔积分法列出的弯矩与绕度关系式即为莫尔定理．莫尔定理常用于辅助其它求解方法来解决超静定问题．下式则为莫尔定理：

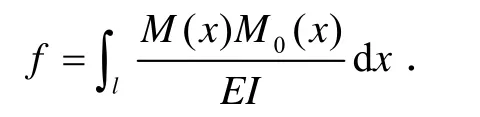
莫尔定理常用于辅助求解，如在下面的叠加法及正则方程解法中就会用到莫尔定理辅助求解．

3.2.3 用力法列变形协调方程

力法是指以未知力为基本未知量的求解方法，这也是超静定结构求解时最常用的方法之一．

3.2.3.1 叠加法列变形协调方程

叠加法属于力法的一种，可以根据叠加原理解超静定问题[3]．

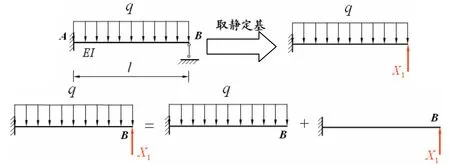
图2 叠加法

如图2，梁的B 点绕度为零．取静定基后可知，B 点的绕度为均匀载荷与支撑力X1迭加作用的结果．然后可以分别查表获得均匀载荷q、支撑力X1与B 点绕度的关系式，联力两个关系式求出X1的值．

3.2.3.2 利用力法—正则方程求解变形协调方程

正则方程是指用标准化的形式来表示变形协调方程．还是以图2 为例，对正则方程进行说明．B 点绕度为零 Δ1=0．

由迭加原理可知

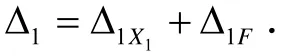
第一个下标1 表示位移发生在X1的作用点，沿着X1的方向．第2个下标X1(或F)表示是由多余反力X1和实际载荷F 引起的．

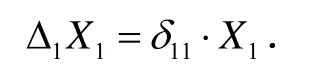
δ11表示X1=1 时，在X1的作用点，沿着X1的方向的位移．因为线弹性体，位移与力成正比，所以X1引起的B 点的位移为δ11的X1倍．

以上公式为一次超静定的力法—正则方程，其中δ11和△1F的值可由莫尔积分求得．

上面介绍的是一次超静定的力法—正则方程，另外还有高次正则方程，用于求解多次超静定结构．下式则为高次正则方程：

其中n 为静不定次数， δij= δj∂是位移互等定理．

4 超静定问题解法举例

例题 如图3，EI 已知，求AB 两铰链的约束．

解 1) 取静定基

如图3 可以去除B 端的可动铰支座的约束，将其用相应的约束力(FB)代替，使梁的形变保持与原来相同的效果，也就是要取静定基．

图3 超静定结构

2) 列补充方程

由图3 可见，B 端的挠度为零，可将其视为均布载荷引起的挠度fBq与未知支座反力fBF的迭加结果(如图4)，其迭加挠度为FB，即：

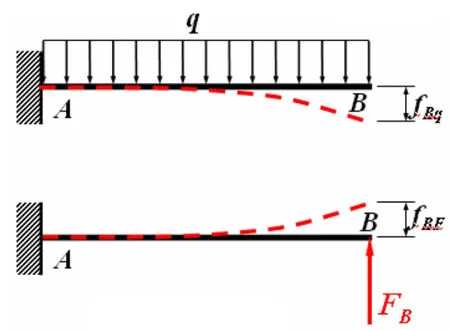
图4 叠加法

查表得力与形变间的物理关系[4]：

将其代入前式得：

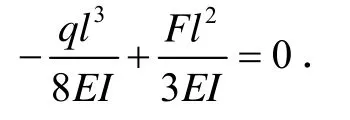
由此解出多余约束反力：

3) 利用平衡方程和补充方程，求得其它支座反力．

5 结语

超静定问题是工程力学中的一个难点，而且不同的求解方法穿插在不同的章节．实践证明，如果采用以上方法，进行系统的总结归纳，将对学生掌握其内容起到很好的促进作用．

[1]刘智,戴少度,张向同.关于静不定结构求位移的证明[J].力学与实践,1992(3):62.

[2]殷安琪.静不定结构解题分析[J].天津轻工业学院学报,1997(2):85-88.

[3]王立新.弯曲中的静不定问题[J].新疆职业大学学报,2003(3):58-59.

[4]张秉荣.工程力学[M].北京:机械工业出版社,2005:28-32．