关于多元多项式的因式分解
2013-10-30姜文英
姜 文 英
(衡水学院 数学与计算机科学学院,河北 衡水 053000)
多元多项式是一元多项式的推广,是多项式理论研究的重要对象.它不但与高次方程的讨论有关,而且在进一步学习代数以及其它数学分支时也都会碰到.多元多项式的因式分解是代数学的一项基本内容,也是数学研究的重要内容之一,又是一个在数学科学中既重要又极为困难的问题,还是符号计算和计算机自动推理中的最基本算法之一.
1 带余除法分解因式
定义[1]若 f ( x1, x2,..., xn)与 g ( x1, x2,..., xn-1)是F [ x1, x2,..., xn]中的任意2个多项式,则存在唯一的一对多项式q ( x1,x2,..., xn)与r ( x1, x2,..., xn-1),使得
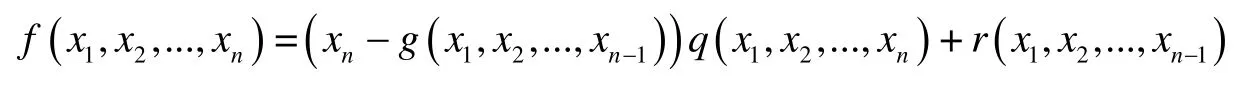
r ( x1, x2,..., xn-1)与q ( x1, x2,..., xn)分别叫做 xn-g ( x1, x2,...,xn-1)除f ( x1, x2,..., xn)所得的余式和商式.
定理1[1]f (x1,x2,..., xn-1, g ( x1, x2,...,xn-1))=0 的充分必要条件是f ( x1, x2,..., xn) 能被 xn-g (x1, x2,...,xn-1)整除.
例1 把多项式x3+ y3+ z3- 3xyz 写成2个多项式的乘积.
解 令 f ( x , y ,z )= x3+ y3+ z3-3xyz ,
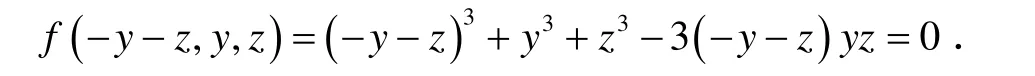
由定理1 知x + y+z 整除 f ( x , y ,z ) ,视x 为未知量, y 、 z 为已知量,用一元多项式里的带余除法,以x + ( y +z)除x3- ( 3yz )x +( y3+z3),有
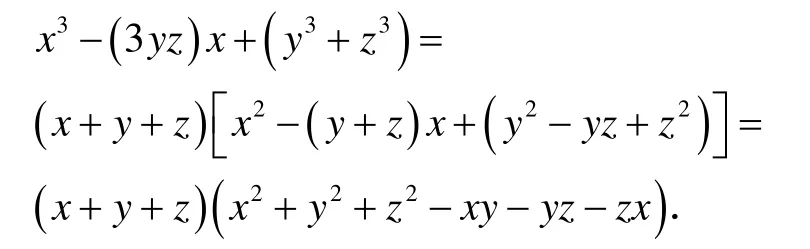
2 二次型法分解因式
定理2[2]一个实二次型 q ( x1, x2,..., xn)可分解为2个实系数 n 元一次齐次多项式的乘积的充要条件是,或者 q的秩等于1,或者 q 的秩等于2 且符号差等于0.
例2 在实数域上分解因式:
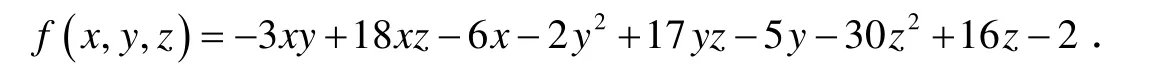
解 令 q ( x , y , z , t ) =-3 xy + 18 xz - 6 xt - 2 z2+ 17yz -5 yt - 30 z2+ 16 zt -2t2, 则f ( x, y ,z )可分解为2个一次多项式的乘积的充要条件是q ( x, y , z ,t )可分解为2个一次多项式的乘积,而

所以 f ( x , y ,z )=(3x + 2 y - 5 z+ 1)(-y + 6 z-2).
3 导数法分解因式
定理[3]关于多项式 F ( x1,x2,..., xn),对于某个 xi( i = 1,2,...,n),若 F 'xi( x1,x2,...,xn)与F (x1, x2,...,xi-1,0, xi+1,...,xn)有公因式,则 F ( x1, x2,..., xn)可以因式分解,且至少有因式d (x1, x2,...,xi-1,0, xi+1,...,xn).
例3 分解因式:( x + y )2( - x + y + z )( z + x - y ) + ( x - y )2(x + y + z )( x + y - z).
解 把 x、 y 看成给定数域 P 中的数,原多项式即是关于 z 的多项式,可以化为:
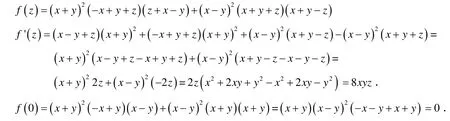
f ' (z )与 f( 0)有公因式,故可以导数法分解f( z ).

因此( x + y )2( - x + y + z )( z + x - y ) + ( x - y )2(x + y + z )( x + y-z )= 4xyz2.
[1]刘功琴.多元多项式的因式分解[J].川北教育学院学报,1998,8(4):67-70.
[2]北京大学数学系几何与代数教研室前代数小组.高等代数[M].3 版.北京:高等教育出版社,2003:233.
[3]贾庆兰.多元多项式的因式分解[J].沧州师范专科学校学报,2004,20(2):41-43.
