局部有限超空间的一致覆盖族

吉 乐,李祖泉

(杭州师范大学理学院,浙江 杭州 310036)

局部有限超空间的一致覆盖族

吉 乐,李祖泉

(杭州师范大学理学院,浙江 杭州 310036)

研究了超空间CL(X)赋予局部有限拓扑的紧致度、特征等相关基数不等式,得到了超空间CL(X)是仿紧空间的充分条件,并利用一致覆盖给出了超空间CL(X)的正规性的刻画.

超空间;局部有限拓扑;紧致度;特征;一致覆盖;正规性

0 引 言

拓扑空间X的非空闭子集超空间CL(X)上有许多拓扑结构, 其中应用最多的是有限拓扑τV, 也称Vietoris拓扑[1]. 局部有限拓扑τlocfin是比有限拓扑更细的一种拓扑, 它是有限拓扑的自然推广. 我们知道, 度量空间X上的超空间Hausdorff拓扑τH等价于有限拓扑τV, 但它不是拓扑不变量. 那么，X上是否存在某个与X的度量无关而只与X的拓扑相关的超空间拓扑？Beer等[2]为了考察这一问题引入了局部有限拓扑,结果证明:度量空间X上的非空闭子集超空间CL(X)的局部有限拓扑等价于X上的所有相容的度量诱导的Hausdorff度量拓扑的上确界.之后,Naimpally等[3-4]获得超空间CL(X)上局部有限拓扑的若干基数不等式.Maio等[5-7]研究超空间CL(X)的第一可数性和紧致度(tightness).宋春玲等[8-9]给出超空间CL(X)上局部有限拓扑的局部紧性和连通性的刻画.本文研究了局部有限拓扑超空间CL(X)的关于紧致度、特征两个基数不等式，得到局部有限拓扑超空间CL(X)的仿紧性的充分条件，并利用一致覆盖给出其正规性的刻画.

1 预备知识

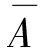
一般地, (CL(X),τlocfin) 不同于 (CL(X),τV). 若ω赋予离散拓扑, 则 (CL(ω),τlocfin) 是离散空间, 从而有 |CL(ω)|=2ω. 因此 (CL(ω),τlocfin) 不是可分空间. 而 (CL(ω),τV) 是非离散的可分空间.

定义2设映射i:X→CL(X)为i(x)={x}.对于超空间CL(X)上的任意拓扑τ,如果i:X→(CL(X),τ)是嵌入映射,这时称超空间(CL(X),τ)是相容的.

引理1对于正则空间X,i:X→(CL(X),τlocfin) 是闭嵌入映射.

这样(CL(X),τlocfin)是相容的.

2 超空间(CL(X),τlocfin)上两个基数不等式

为了刻画超空间(CL(X),τlocfin)上两个基数t(CL(X),τlocfin)和χ(CL(X),τlocfin),类似于文献[13]中给出的基数klo(X)和kko(X),我们给出clco(X)和ccco(X)的定义.

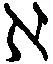
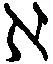
定理1对于空间X，有clco(X)≤t(CL(X),τlocfin).

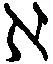
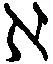
定理2对于空间X,有ccco(X)≤χ(CL(X),τlocfin).

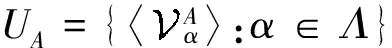
3 超空间(CL(X),τlocfin)的仿紧性

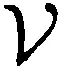
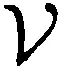
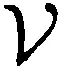
容易证明:每个紧空间是c-仿紧的.

定理3每个c-仿紧空间的闭子集是c-仿紧的.

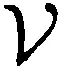
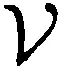
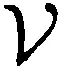
定理4若X是c-仿紧的,则(CL(X),τlocfin)是仿紧空间.

推论1若X是c-仿紧空间,则X是仿紧空间.

证明由定理4,(CL(X),τlocfin)是仿紧空间.再由引理1,X是(CL(X),τlocfin)的闭子集.而仿紧性具有闭遗传性,所以X是仿紧空间.

4 超空间(CL(X),τlocfin)的一致覆盖族

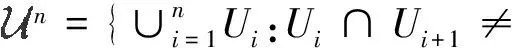
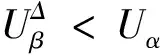
2)存在仅由X的开覆盖组成该一致覆盖族的基.

引理5[12]设(X,τ)是完全正则空间,则X上存在导出τ的一致覆盖族的基.

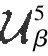
定理7设(X,τ)是完全正则空间,则下列条件等价:

1)(X,τ)是正规空间;

2)τeΦ=τlocfin.

[1] Michael E. Topologies on spaces of subsets[J]. Trans Math Soc,1951,71(1):152-182.

[2] Beer G A, Himmelberg C J, Prikry K,etal. The locally finite topology on 2X[J]. Proc Amer Math Soc,1987,101:163-172.

[3] Naimpally S A, Sharma P L. Fine uniformity and the locally finite hyperspace topology[J]. Proc Amer Math Soc,1988,103:641-646.

[4] Bella A. Some cardinality properties of a hyperspace with the locally finite topology[J]. Proc Amer Math Soc,1988,104:1274-1278.

[5] Maio G D, Holá L, Pelant J. Properties related to the first countability of hyperspace topologies[J]. Question and Answer in General Topology,2001,19(1):139-157.

[6] Maio G D, Koĉinac L D R, Meccariello E. Selection principles and hyperspace topologies[J]. Topology and its Applications,2005,153(516):912-923.

[7] Maio G D, Koĉinac L D R. Some covering properties of hyperspaces[J]. Topology and its Applications,2008,155(17/18):1959-1969.

[8] 宋春玲,谢琳,夏尊辁.局部有限超拓扑的局部紧性[J].数学研究与评论,2004,24(4):705-709.

[9] 谢琳,宋春玲.局部有限超拓扑的连通性[J].辽宁师范大学学报:自然科学版,2001,24(2):120-122.

[10] Engelking R. General topology[M]. Warszwa: Polish Scientific Publishers,1977:373-391.

[11] 儿玉之宏,永见启应.拓扑空间论[M].方嘉琳，译.北京:科学出版社,2001:133-141.

[12] 高国士.拓扑空间论[M].2版.北京:科学出版社,2008:112-123.

[13] Hou Jicheng. Character and tightness of hyperspaces with the fell topology[J]. Topology and its Applications,1998,84:199-206.

UniformCoverFamiliesofLocallyFiniteHyperspace

JI Le, LI Zuquan

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

This paper discussed some cardinal inequalities such as tightness and characters of hyperspace CL(X) for locally finite topology, obtained a sufficient condition of CL(X) being paracompact, and gave a characteristic of normality on CL(X) by uniform covers.

hyperspace; locally finite topology; tightness; character; uniform cover; normality

2012-12-12

李祖泉(1963—)，男，教授，主要从事一般拓扑学研究.E-mial:hzsdlzq@sina.com

10.3969/j.issn.1674-232X.2013.04.011

O189.11MSC201054B20；54E15

A

1674-232X(2013)04-0338-05