非线性热传导方程的反演计算

杨 浩，赵丽玲

(杭州师范大学理学院，浙江 杭州 310036)

非线性热传导方程的反演计算

杨 浩，赵丽玲

(杭州师范大学理学院，浙江 杭州 310036)

讨论非线性热传导方程确定未知热导率分布的反问题.由于热导率与空间和时间有关，先将非线性方程近似转化成线性方程，再通过中心差分离散，采用步进格式得到求解网格节点温度的迭代方程并讨论迭代方程的数值稳定性，最后结合广义交叉校验(GCV)准则和Tikhonov正则化方法，反演计算出与空间位置和温度有关的热导率.数值模拟结果表明该方法可行有效.

热传导方程；反问题；正则化方法

热传导参数反演问题[1]主要是从温度场的某些观测信息来获取介质本身的热传导的性质，即从给定集合上的解来确定热传导方程的未知系数.对于反系数问题(与位置和温度有关的热导率a(x,U) 的非线性热传导方程反演计算问题)，文献[2-4]对热传导方程的反演计算也进行了一些研究，在此基础上本文对一些非线性热传导方程进行反演计算，从而为热传导参数的确定提供了更加完善的解决方案.

1 问题模型离散及迭代格式

(1)

其中a(x,U)为待求未知量.

采用均匀的网格剖分如下:

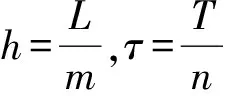
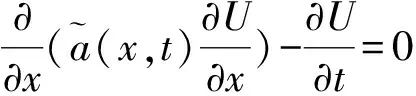
(2)

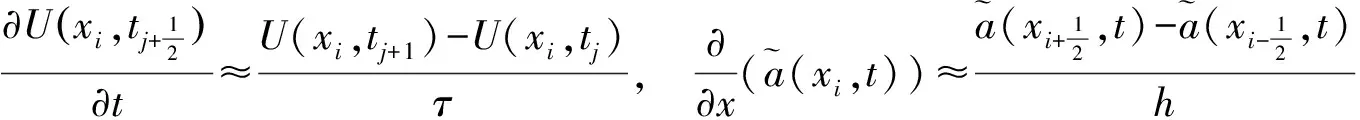
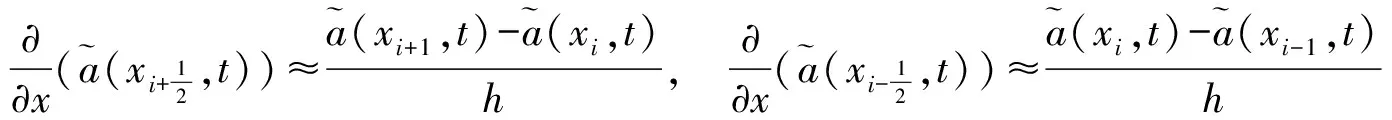
则得到

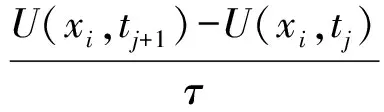
(3)

再次取如下形式近似:

则式(3)化为

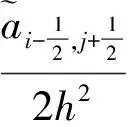
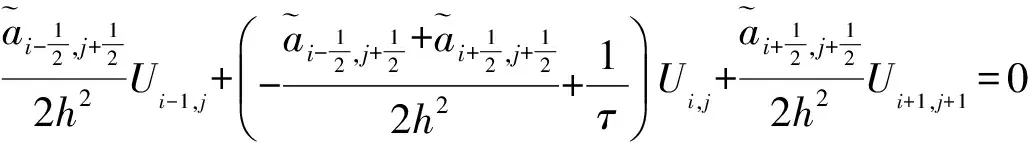
(4)

在x=0和x=L处离散边界条件可得

故

当j=0时，U(x,0)=0，式(4)可化为

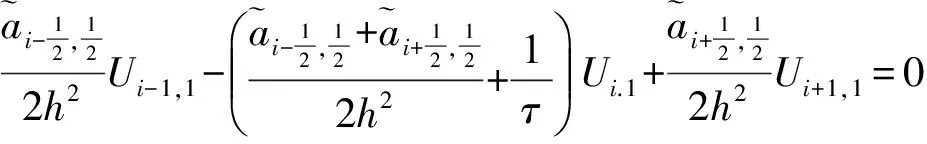
当i=0时，

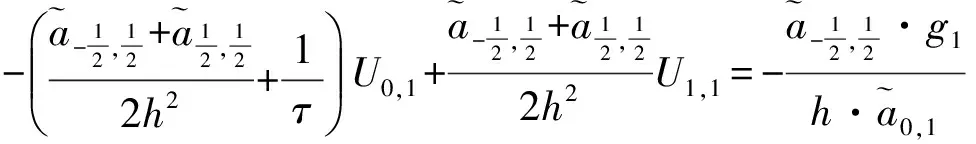
当i=m时，

当1≤i≤m-1时，

写成矩阵方程组即

Q1·U1=V1,

(5)

这里Q1是(m+1)×(m+1)阶严格三对角占优矩阵.其中：

当1≤j≤n-1时，式(4)化为

当i=m时，式(4)化为

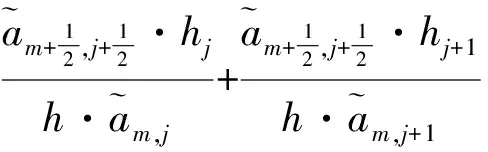
当1≤i≤m-1时，即为式(4).把离散格式写成矩阵方程组的形式，则有

Qj+1·Uj+1=Wj+1·Uj+Vj+1，

(6)

其中：Qj+1是(m+1)×(m+1)阶严格三对角占优矩阵，Wj+1是三对角矩阵，

Uj=[U0,j,U1,j,U2,j,…,Um,j]T,

另外Qj+1和Wj+1可改写为：

(7)

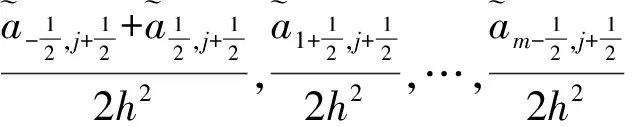
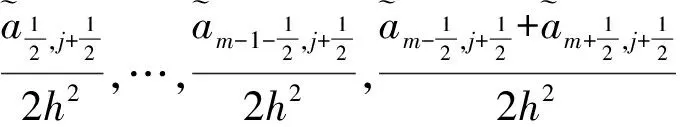
2 迭代增量Δb0,Δb1,Δb2,Δb3

误差函数：

(8)

这里选择函数类：

(9)

为了使T最小，令T关于b0,b1,b2,b3的偏导数均为零，即

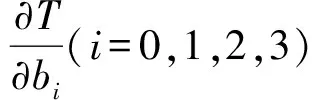
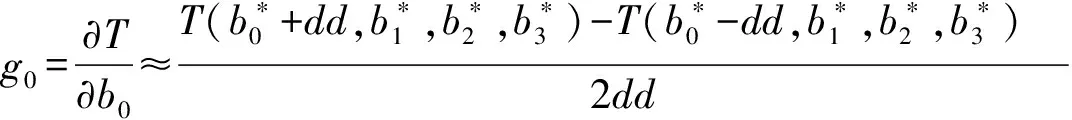
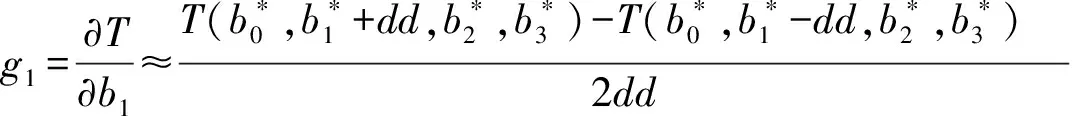
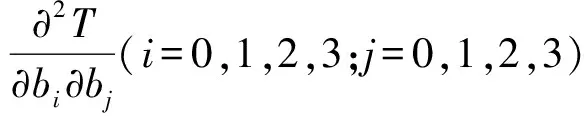
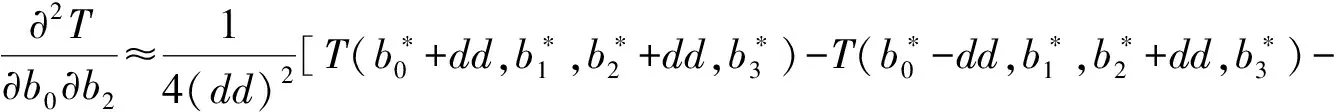
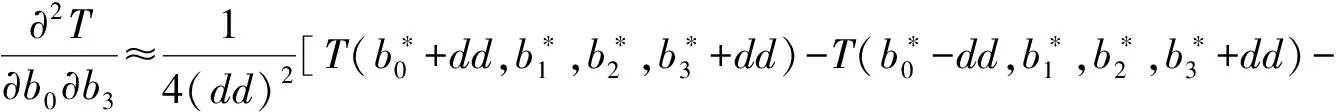
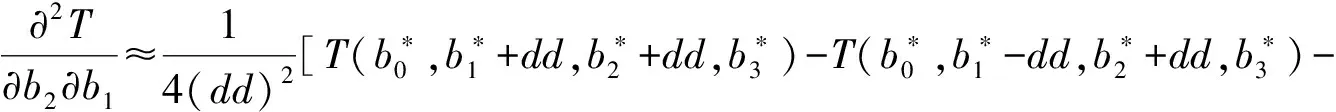
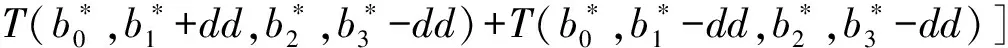
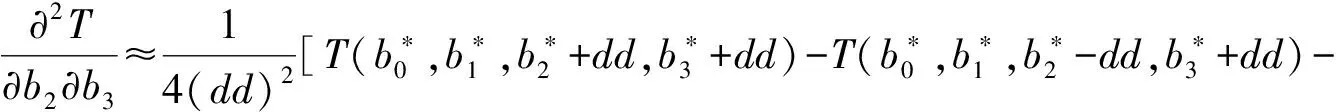
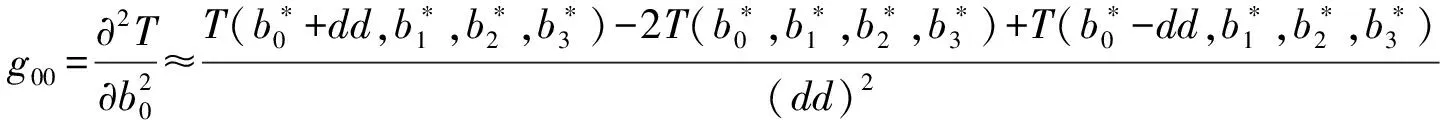
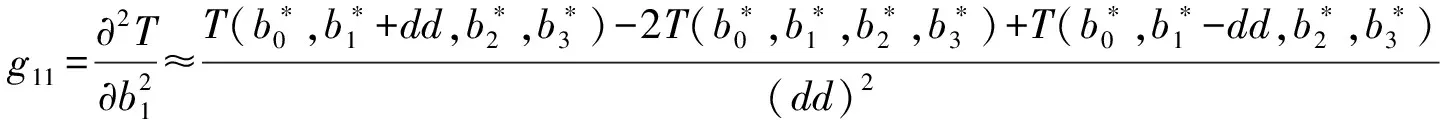
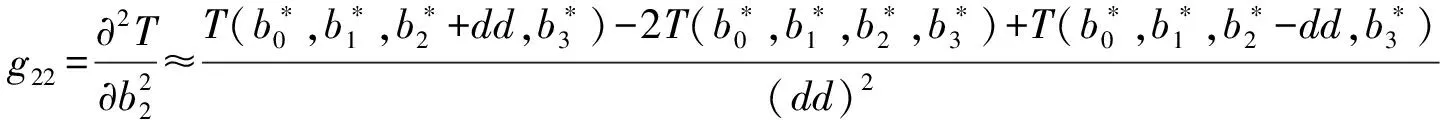
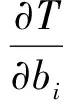
(10)

其中Δb0,Δb1,Δb2,Δb3为b0,b1,b2,b3的迭代改善增量,dd是偏导数的离散步长，关于b0,b1,b2,b3取相同的离散步长dd.

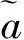
3 数值试验

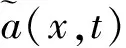
例1设a(x,u)=1,

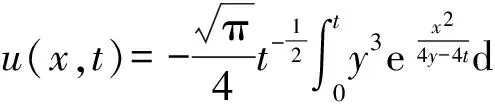
这里在空间和时间上采用相同的m=n等分的网格剖分，如表1-表2所示，表中第一列为牛顿迭代格式离散步长的取值dd，b,c皆为正则化后的结果.

表1 m=n=10，不同的dd误差的变化，aerror=0.5772

表2 m=n=20，不同的dd误差的变化，aerror=0.5653

例2设a(x,u)=t,

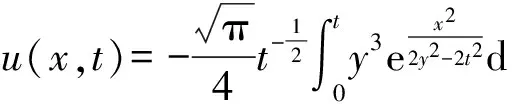
这里在空间和时间上采用相同的m=n等分的网格剖分，如表3-表4所示.

表3 m=n=10，不同的dd误差的变化，aerror=0.4667

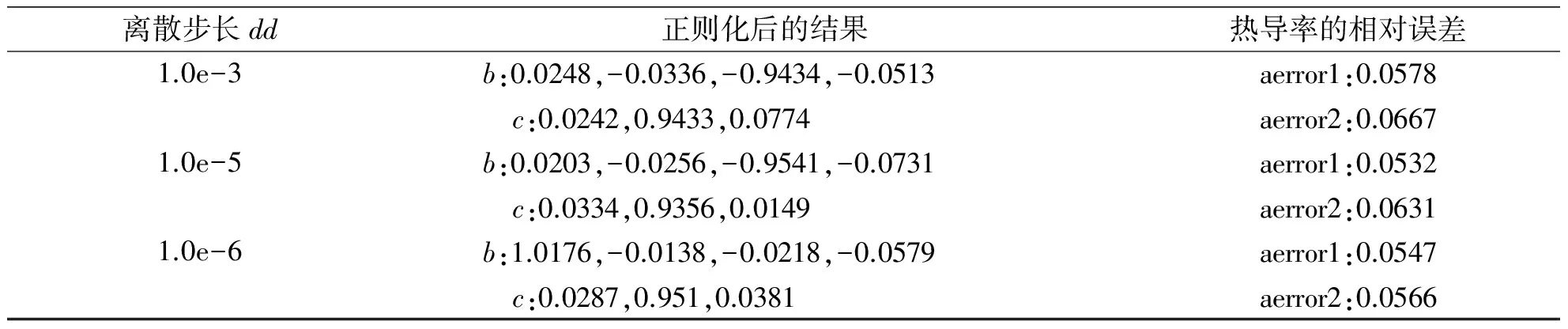
表4 m=n=20，不同的dd误差的变化，aerror=0.4513

例3设a(x,u)=u,

即热导值的精确解为[b0,b1,b2,b3]=[0,1,1,1],[c0,c1,c2]=[0,0,1].初始值选为[b0,b1,b2,b3]=[0.1,0.9,0.9,0.9].

这里在空间和时间上采用相同的m=n等分的网格剖分，如表5、图1-图2所示.通过比较表5以及图1-图2，当给定初始值，初始误差为0.5000，经过适当的离散，正则化计算后的误差可以降至0.0611.

表5 m=n=10，不同的dd误差的变化，aerror=0.5000

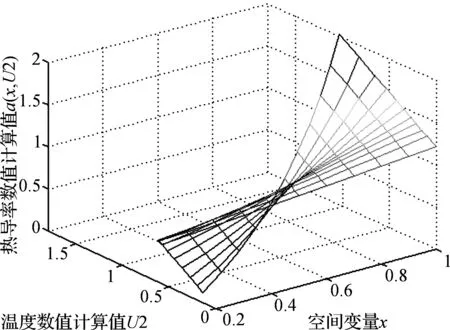
图1 m=n=10时，初值为[0.5,0.5,0.5,0.5],dd=1.02e-5时，a(x,U)的图像Fig. 1 Picture of a(x,U), when m=n=10, initial value is [0.5,0.5,0.5,0.5], dd=1.02e-5

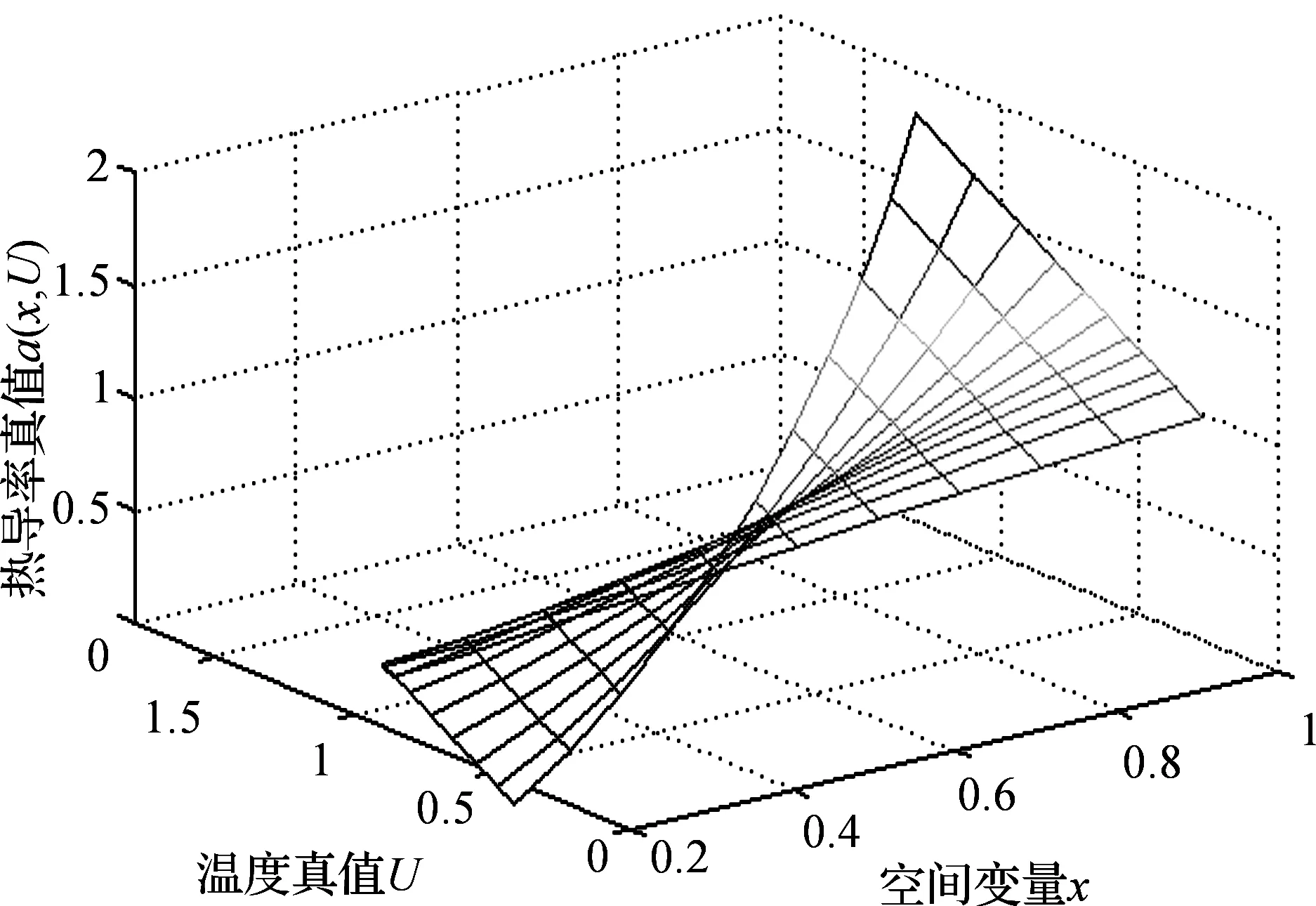
图2 m=n=10时，初值为[0.01,0.98,1.02,0.97],dd=1.02e-5时，a(x,U)真值的图像Fig. 2 Picture of true value of a(x,U), when m=n=10, initial value is [0.01,0.98,1.02,0.97], dd=1.02e-5

4 结 论

本文主要研究了齐次非线性热传导方程的反演计算的数值稳定性，经过本文的方法计算后误差已经相对较小，逼近效果也很好，可见本文的方法是非常有效的.

[1] Masataka T.Abstracts of international symposium on inverse problems in engineering mechanics (ISIP) [M]. Nagano City:Symposium secretariat,2000:1-52.

[2] Zhu Jianxin. Inverse computation of heat conductivity with surface measurable data[C]// Yao Jianquan,Chen Y J,Seok L.Semiconductor Lasers and Applications II.Bellingham WA:SPIE, 2005,5628:143-149 .

[3] 周曼.一类热导率的反演数值解法[D].杭州:浙江大学,2007.

[4] 钱炜祺,蔡金狮,任斌.二维稳态热传导逆问题初步研究[J].计算物理，2002,19(6):512-516.

[5] 王振宇,刘国华.走时层析成像的迭代Tikhonov正则化反演研究[J].浙江大学学报：工学版,2005,39(2):259-263.

InverseCalculationofNonlinearHeatConductionEquation

YANG Hao, ZHAO Liling

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

This paper discussed the inverse problems of determining unknown heat conductivity distribution by nonlinear heat conduction equation. Because of the links among heat conductivity, space and time, the nonlinear equations were firstly approximately converted into linear equations. Then, through the separation of the equation of center, the paper obtained the iterative equations for solving the temperature of grid nodes with marching method, discussed the numerical stability of the iterative equations, and finally inversely calculated the heat conductivity which concerning space and temperature by combing generalized cross check (GCV) with Tikhonov regularization method. The numerical simulation results show that the treatment is feasible and efficacious.

heat conduction equation; inverse problem; regularization method

2013-02-28

赵丽玲(1985—),女，应用数学专业硕士研究生,主要从事科学计算研究.E-mail:284183733@qq.com

10.3969/j.issn.1674-232X.2013.04.013

O174.41MSC201047H10；54H25

A

1674-232X(2013)04-0347-07