Lorentz空间型中具有平行Ricci曲率的类空超曲面
2013-10-28何百通宋卫东
耿 杰,何百通,宋卫东
(1. 安徽师范大学数学计算机科学学院,安徽 芜湖 241003;2. 衢州职业技术学院基础部,浙江 衢州 324000)
耿 杰1,何百通2,宋卫东1
(1. 安徽师范大学数学计算机科学学院,安徽 芜湖 241003;2. 衢州职业技术学院基础部,浙江 衢州 324000)

Lorentz空间;平行Ricci曲率;常平均曲率;类超曲面;积分不等式
1 引言及主要结论


其中:
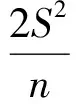
2 预备知识
本文对各类求和指标取值范围约定如下
1≤A,B,C,…≤n+1;1≤i,j,k,…≤n.
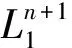
dωA=∑εBωAB∧ωB,ωAB+ωBA=0,

KABCD=εAεB(δACδBD-δADδBC)c,
(1)
其限制到Mn上[5]
(2)
(3)
(4)
Rijkl=Kijkl-∑(hikkjl-hilhjk),
(5)
Kijkl=(δikδjl-δilδjk)c,
(6)
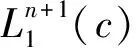

下面用hijk,hijkl表示hij的共变导数,定义hijkωk=dhij+∑hkiωkj+∑hjkωki,
hijklωl=dhijk+∑hljkωli+∑hilkωlj+∑hijlωlk.
(7)
则Mn的Codazzi方程[5]为
hijk-hikj=-Kn+1ijk=0,
(8)
及Mn的Ricci方程[5]为

(9)
由(8)(9)得
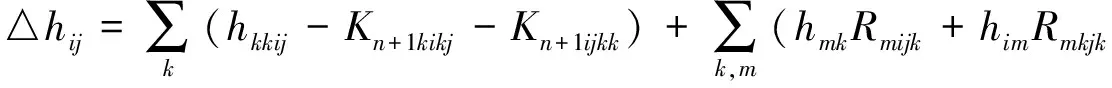
(10)
由(1)得,Kαijk=0,故Kαijkl=0.
由于hkkij=0,再根据(10)得

(11)
由(5)(6)(11)得
(12)
Mn的Ricci曲率张量为[4]
(13)
由于Mn的Ricci曲率平行,且H为常数(其中H≥0),所以[4]
Rij,k=0.


(14)
又因为

(15)
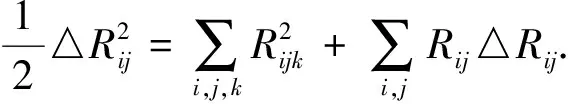
(16)
3 定理的证明
由(12)(13)(15)(16)得


(17)
有

(18)


-2n2H2c2(n-1)-2n(n-1)cHtrA3-2cS(n-1)(nc+S),
(19)
其中trA表示矩阵A=(hij)n×n的迹.

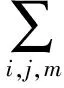
=-n4H4c-n3H3trA3+n2H2(nc+S)S.
(20)
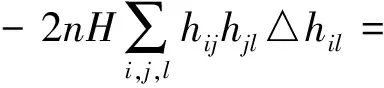
=2n2H2cS+2n2H2trA4-2nH(nc+S)trA3.
(21)
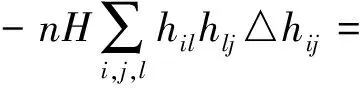
=n2H2cS+n2H2trA4-nH(nc+S)trA3.
(22)
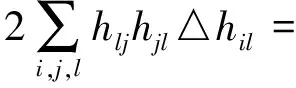
2(nc+S)trA4.
(23)
由(14)得
(24)
(25)
由于[5]

(26)
由(18)-(26)得
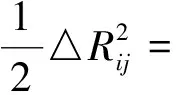
2c(n-1)(nc+S)S-[n3H3+3nH(nc+S)+2n(n-1)Hc]trA3+

(27)


同理可得:

(28)
将(26)(28)代入(27),经过化简得


(29)
根据散度定理及Hopf引理,得
(30)
其中:

[1] 郭震.李奇曲率平行的黎曼流形到欧氏空间的等距浸入[J].数学学报,1998,41:1108-1112.
[2] 李同柱,郭震.常曲率流形中具平行李奇曲率的超曲面[J].数学学报,2004,47:587-592.
[3] 成庆明.Lorentz流形中的类空超曲面[J].数学季刊,1991(4):1-5.
[4] 钟定兴,肖卫玲.Lorentz空间型中具有平行Ricci曲率的类空超曲面[J].赣南师范学院学报,2007(3):8-11.
[5] 冯维.一般伪黎曼流形中的极大类空子流形[J].浙江大学学报:理学版,2003.32(2):132-134.
HypersurfaceswithParallelRicciCurvatureinLorentz-typeSpace
GENG Jie1, HE Baitong2, SONG Weidong1
(1. College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China;2. Foundation Department of Quzhou College of Technology, Quzhou 324000, China)
Lorentz space; parallel Ricci curvature; constant mean curvature; space-like hypersuface; integral inequality
2012-10-25
安徽省教育厅自然科学基金重点项目 (KJ2010A125);浙江省新世纪高等教育教学改革项目(2010074).
宋卫东(1958—),男,教授, 主要从事微分几何研究.E-mail:swd56@sina.com
10.3969/j.issn.1674-232X.2013.02.007
O186MSC201053B30,53A10
A
1674-232X(2013)02-0124-04
