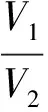人口有增长传染病模型的周期解
2013-10-28鲁世平
高 芳,鲁世平
(安徽师范大学数学计算机科学学院,安徽 芜湖 241003)
人口有增长传染病模型的周期解
高 芳,鲁世平
(安徽师范大学数学计算机科学学院,安徽 芜湖 241003)
本文利用重合度理论和一些分析技巧讨论了一类人口有增长传染病模型, 得到了其周期解存在性的新结论.
人口增长;传染病;周期解;重合度
0 引 言
近几十年来, 传染病动力学的研究进展迅速, 大量的数学模型被用于分析各种各样的传染病问题[1-5].如:研究具有暂时免疫传染病带有隔离的传染病;具有脉冲出生和脉冲接种的传染病;具有垂直传染病等等. 在讨论传染病模型时,一般多假设在所研究的区域内,任何时间人口总数不变,即人口出生率与死亡率相等,而在文献[6]中考虑了人口有增长的传染病模型:



其中:S=S(t)表示t时刻易感冒者数目,I=I(t)表示t时刻染病者数目;R=R(t)表示t时刻消除者数目, 记t时刻总人数为N=N(t)=S(t)+I(t)+R(t),β>0为传染率,r>0为移除率;a>0表示3类人共有的死亡率;α>0代表因传染病而死亡的死亡率;v>0代表R类人免疫率的丧失率.
根据实际问题需要考虑环境变化的影响,则考虑下列非自治模型:

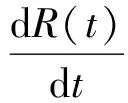

(1)
在此假设所有的变系数都是正ω周期函数, 本文将利用重合度系统的正定理来讨论系统(1)正ω周期解的存在性.
1 引 理
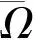
1) 对任意的λ∈(0,1),x∈ ∂Ω∩D(L),均有Lx≠λNx;
2) 对任意的x∈ KerL∩ ∂Ω,均有QNx≠0;

为方便起见, 对连续的正Ω周期函数g(t),记gL=min[0,ω]g(t),gM=max[0,ω]g(t)
2 主要结果

证明令I(t)=eu1(t),R(t)=eu2(t),N(t)=eu3(t),则系统(1)变为
u1′(t)=-(α(t)+b(t)+r(t))+β(t)eu3(t)-β(t)eu1(t)-β(t)eu2(t),u2′(t)=r(t)eu1(t)-u2(t)-(b(t)+v(t)),
u3′(t)=(a(t)-b(t))-α(t)eu1(t)-u3(t),
(2)
分别定义算子
L:D(L)⊂X,Lu=u′,N:X→X,
其中X=Cω={u(t)=(u1(t),u2(t),u3(t))T∈C(R,R3):u(t+ω)≡u(t)},记||u(t)||=max|u1(t)|+max|u2(t)|+max|u3(t)|,D(L)={u(t)=(u1(t),u2(t),u3(t))T∈C(R,R3):u(t+ω)≡u(t)}⊂X,显然X为Banach空间. 易见方程可以转化为算子方程Lu=Nu.


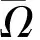
记Ω1={u:u∈D(L)⊂Cω,Lu=λNu,λ∈(0,1)},∀u∈Ω1,得
u1′(t)=λ[-(α(t)+b(t)+r(t))+β(t)eu3(t)-β(t)eu1(t)-β(t)eu2(t)],u2′(t)=λ[r(t)eu1(t)-u2(t)-(b(t)+v(t))],
u3′(t)=λ[(a(t)-b(t))-α(t)eu1(t)-u3(t)],
(3)
因为u(t)=(u1(t),u2(t),u3(t))T∈X,所以存在ξi,ηiε[0,ω](i=1,2,3)使得

则显然得到u1(ξ1)′=u1(η1)′=0,u2(ξ2)′=u2(η2)′=0,u3(ξ3)′=u3(η3)′=0,
由系统(3)的第一个式子得:
(α+b+r)L≤α(ξ1)+b(ξ1)+r(ξ1)=β(ξ1)eu3(ξ1)-β(ξ1)eu1(ξ1)-β(ξ1)eu2(ξ1),
所以
β(ξ1)eu1(ξ1)≤β(ξ1)eu3(ξ1)-β(ξ1)eu2(ξ1)-(α+b+r)L≤β(ξ1)eu3(ξ1)≤βMeu3(ξ3),
所以
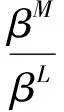
(4)
再由系统(3)的第二个式子得:(b+v)L≤b(ξ2)+v(ξ2)=r(ξ2)eu1(ξ2)-u2(ξ2)≤rMeu1(ξ1)-u2(ξ2),
则
(b+v)Leu2(ξ2)≤rMeu1(ξ1),
(5)
又因为由系统(3)得:(a-b)L≤a(ξ3)-b(ξ3)=α(ξ3)eu1(ξ3)-u3(ξ3)≤αMeu1(ξ1)-u3(ξ3),
则
eu3(ξ3)(a-b)L≤αMeu1(ξ1).
(6)
再将(6)代入(4)有
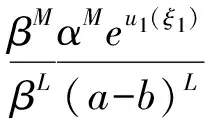
(7)
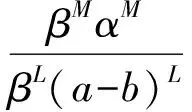
由(5)(6)有

(8)
同理:
(α+b+r)L≤α(η1)+b(η1)+r(η1)=β(η1)eu3(η1)-β(η1)eu1(η1)-β(η1)eu2(η1)≤β(η1)eu3(η1)+β(η1)eu1(η1)+β(η1)eu2(η1)≤βMeu3(ξ3)+βMeu1(η1)+βMeu2(ξ2)=βM(R2+R3)+βMeu1(η1),
βMeu1(η1)≥(α+b+r)L-βM(R2+R3),
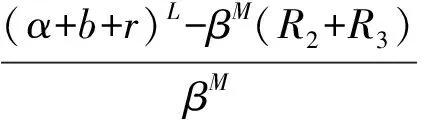
(9)
同理
(b+v)Meu2(η2)≥rLeu1(η1),
则
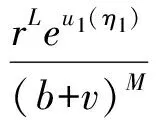
(10)
同理

(11)
由(7)-(11)知
u1(ξ1)≤lnR1,u2(ξ2)≤lnR2,u3(ξ3)≤lnR3,u1(η1)≥lnL1,u2(η2)≥lnL2,u3(η3)≥lnL3,
则对任意t∈[0,ω],有|ui(t)| 在定理1的条件成立时, 代数方程组 令Ω={u(t)=(u1(t),u2(t),u3(t))T∈X,||u(t)|| 当u∈∂Ω∩KerL时u是一个常向量, 且||u||=B,所以QNu≠0. 另一方面令J:ImQ→KerL满足J(u)=u,作同论φ(u,μ)=-μu+(1-μ)JQNu,μ∈[0,1], 则有 deg{JQN,Ω∩KerL,0}≠0, 所以由定理知系统存在ω周期解. [1] Li Jianquan, Ma Zhien. Qualitative analyses of SIS epidemic model with Vaccination and Varying total Population Siza [J].Mathematical and Computer,2002,35(11-12):1235-1243. [2] Hwthcote H W.The Mathematics of infentius diseases [J]. SIAM Review,2000,42(4):599-653. [3] Song Xinyu, Wang Shaoli. Stability properties and Hopf bifurcation of a delayed viral infection model with lytic immune response[J]. J Math Anal Appl,2010,373(2):345-355. [4] Kuang Yang. Delay differential equation with applications in population dynamics[M]. New York:A cademicpress,1993. [5] 李武,林师仲.具有外来感染者和急慢性阶段流行病模型的周期解[J].数学的实践与认识,2009,39(8):101-105. [6] 岳锡亭,潘家齐.人口有增长传染病模型的定性分析[J].长春工业大学学报:自然科学版,2003,24(3):1-4. PeridicSolutionsofPopulationGrowthEpidemicModel GAO Fang, LU Shiping (College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China) This paper studied a class of population growth epidemic model by means of an continuation degree theorem and some analysis methods, and obtained new results on the existence of periodic solutions. population growth; epidemic model; peridic solutions; coincidence degree 2012-10-22 教育部科研基金项目(207047);安徽省应用数学重点学科基金项目(2009-2014). 鲁世平(1962—),男,教授,博士,主要从事泛函分析研究. E-mail:lushiping26@sohu.com 10.3969/j.issn.1674-232X.2013.02.008 O175.1MSC201034K13;34K60 A 1674-232X(2013)02-0128-03