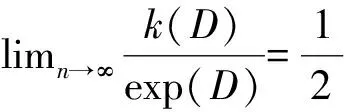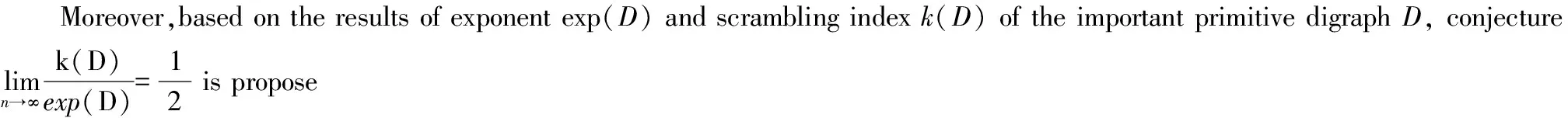本原有向图Dn,q,s的scrambling指数
2013-10-27尤利华
尤利华, 陈 芳
(华南师范大学数学科学学院,广东广州 510631)
本原有向图Dn,q,s的scrambling指数
尤利华*, 陈 芳
(华南师范大学数学科学学院,广东广州 510631)
本原有向图; scrambling 指数; 缺数段; 指数集
称有向图D是本原的,如果存在正整数k,使得对于D中的任意2点vi和vj(允许i=j),在D中都存在从点vi到点vj长为k的有向途径.这样的最小正整数k称为D的本原指数,记为exp(D).众所周知,有向图D是本原的当且仅当D是强连通的且其所有圈长的最大公约数(简记为g.c.d.)为1.记所有的n阶本原有向图的集合为Pn.
AKELBEK和KIRKLAND[1]给出了有向图的scrambling指数和局部scrambling指数的定义. 事实上,scrambling指数和局部scrambling指数与PAZ[2]定义的公共后续指数及局部公共后续指数是一回事. 当有向图是本原有向图时,它们与文献[3]定义的有向图的竞赛指数的定义是一样的. 关于其研究进展,可参见文献[1]-[16].
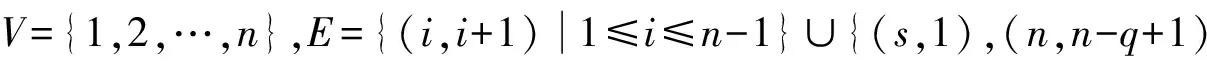
显然Dn,q,s是本原有向图. 事实上,Dn,q,s是组合矩阵论中一类重要的(极)图.例如:文献[18]在研究本原有向图的本原指数时,Dn,n,n-1就是取到本原指数最大值(n-1)2+1的图D1;文献[19]在研究本原几乎可约有向图的本原指数时,Dn,n-1,s就是取到其本原指数最大值n+s(n-3)的图Dn-1,s;文献[17]在研究本原有向图的Lewin数时,Dn,n-1,s就是取到Lewin数最大值的图Dn-1,s;在本原有向图的局部指数和其带号有向图的基指数的研究中所涉及到的极图也是图类Dn,q,s中某些具体的图[18,20].同样,在研究本原有向图的scrambling指数和m-competition指数时其极图也是Dn,q,s中某些具体的图[1,5-6,8-9,11-13,15-16],等等.
本文研究了本原有向图Dn,q,s的scrambling指数,提出了1个公开问题.
1 本原有向图Dn,q,s的scrambling指数
引理1[1]设q,s是两正整数,满足g.c.d.(q,s)=1,2≤s 注1 在文献[1]中,由引理1的证明易知方程xq+ys=t的具有最小绝对值的整数解就是满足xq+ys=t且|x|≤⎣s/2」,|y|≤⎣q/2」的整数解. 引理2[1]设D是n阶本原有向图,q,s是D的两不同的圈长,若g.c.d.(q,s)=1,2≤s ku,v(D)≤min{|y|s,|x|q}+lu,v, (1) 注2 由于|y|≤⎣q/2」,|x|≤⎣s/2」,所以 ku,v(D)≤min{|y|s,|x|q}+lu,v≤ min{⎣q/2」s,⎣s/2」q}+lu,v. (2) 记Dn,q,s中长为s,q的圈分别为Cs,Cq. 以下,令U=V(Cs)∩V(Cq)={n-q+1,…,s}. 因为q+s≥n+1,故U≠.以下以d(u,v)表示有向图中点u到点v的最短路的长度. 引理3 设n,q,s,Dn,q,s如上文所定义,则 k(Dn,q,s)≤min{⎣q/2」s,⎣s/2」q}+n-s= (3) 证明当s=1时,k≤n-1,结论成立. 当s≥2时,以下分6种情形: ki, j(Dn,q,s)≤min{⎣q/2」s,⎣s/2」q}+n-s. (4) 对于情形1~情形3,均取n-q+1为双圈点,则li, j=max{l(i,n-q+1),l(j,n-q+1)}≤n-s, 由引理2知式(4)成立.下面证明在情形4~情形6下式(4)成立. 子情形4.1:s是奇数. 子情形4.2.2:1≤t 子情形4.2.3:t>s/2.此时d(j,i)=s-t,且s-t 子情形5.1:s是奇数. 子情形5.1.1:若xq-ys=t.此时同子情形4.1.1的证明. 子情形5.2:s是偶数.此时由g.c.d.(q,s)=1知q必为奇数,从而y≤(q-1)/2. 子情形5.2.1:若ys-xq=t.此时同子情形4.2.2.2的证明. 子情形5.2.2:若xq-ys=t.此时1≤t=d(i,j)≤s-1,可分以下3种情形证明. 子情形5.2.2.1:若1≤t 子情形5.2.2.3:若t=s/2,则 (1)若s/2≤n-s.此时取j为双圈点,则li, j=max{l(i,j),l(j,j)}≤n-s,再由引理2得 子情形6.1:s是偶数.此时q必为奇数.以下分2种情形证明. 子情形6.1.1:若d(j,i)≤n-s.取i为双圈点,则li, j=max{l(i,i),l(j,i)}≤n-s,再由引理2知 子情形6.2:s是奇数. 子情形6.2.1:若d(j,i)≤n-s.此时同子情形6.1.1的证明. 子情形6.2.2:若d(j,i)≥n-s+1.此时类似于子情形6.1.2的证明. □ □ 以下以p(u,v)表示有向图中点u到点v的有向路的长度. □ (1)若p(s+1,n-q+1)>p(v,n-q+1),记p(s+1,n-q+1)-p(v,n-q+1)=t1s+d1,其中t1,d1为非负整数且0≤d1≤s-1. (i)当d1≥1且存在非负整数x,y,x≤⎣s/2」,y≤⎣q/2」,使得xq-ys=d1,则 ks+1,v(Dn,q,s)=xq+p(v,n-q+1)=(y-t1)s+n-s. (ii)当d1≥1且存在非负整数x,y,x≤⎣s/2」,y≤⎣q/2」,使得ys-xq=d1,则 ks+1,v(Dn,q,s)=xq+n-s=(y+t1)s+p(v,n-q+1). (2)若p(s+1,n-q+1) (iii)当d2≥1且存在非负整数x,y,x≤⎣s/2」,y≤⎣q/2」,使得ys-xq=d2,则 ks+1,v(Dn,q,s)=xq+p(v,n-q+1)=(y+t2)s+n-s. (iv)当d2≥1且存在非负整数x,y,x≤⎣s/2」,y≤⎣q/2」,使得xq-ys=d2,则 ks+1,v(Dn,q,s)=xq+n-s=(y-t2)s+p(v,n-q+1). 证明首先由引理4可知点s+1与点v通过最短的相同途经长所到达的公共点为n-q+1,故ks+1,v(Dn,q,s)等于点s+1与点v到达公共点n-q+1的最短相同途经长. 注意到点s+1到点n-q+1只有唯一的一条路,故p(s+1,n-q+1)=n-s,设W1、W2是点s+1与点v到达公共点n-q+1的2条同长途径,则W1(W2)是点s+1(点v)到点n-q+1的有向路与若干个圈之并,从而有非负整数x1,x2,y1,y2使 下面先证明(i)和(ii)成立. 情形1:若x2≥x1.下证y2 从而(x2-x1)q+(y2-y1)s=t1s+d1,其中x2-x1和y2-y1均为非负整数. 由引理5知p(s+1,n-q+1)-p(v,n-q+1)=t1s+d1 故有(x2-x1)q-(y1-y2+t1)s=d1.此时,若存在非负整数x,y,x≤⎣s/2」,y≤⎣q/2」,使得xq-ys=d1,则由注1知ks+1,v(Dn,q,s)=xq+p(v,n-q+1)=(y-t1)s+n-s,即(i)成立. 情形2:若x2 故有(y2-y1-t1)s-(x1-x2)q=d1.此时,若存在非负整数x,y,x≤⎣s/2」,y≤⎣q/2」,使得ys-xq=d1,则由注1知ks+1,v(Dn,q,s)=xq+n-s=(y+t1)s+p(v,n-q+1),即(ii)成立. 结论(iii)、(iv)的证明与以上证明类似,故略去. □ 引理7 设n,q,s,Dn,q,s如上文定义,记 则 证明情形1:若s是偶数. 此时q必定为奇数,可分如下2种情形证明. 子情形1.2.1: 若p(v,n-q+1)=n-s/2.此时p(v,n-q+1)-p(s+1,n-q+1)=s/2. 再由sq/2-(q-1)s/2=s/2及引理6之(iv)可知此情形下点s+1与点v到点n-q+1的最短相同途径长为(q-1)s/2+n-s/2. 子情形1.2.2: 若p(v,n-q+1)=n-3s/2+q.此时p(v,n-q+1)-p(s+1,n-q+1)=q-s/2≤n-s/2≤3s/2-s/2=s.再由(q,s)=1知q-s/2=s当且仅当s=2,n=q=3,可直接验证结论成立.以下仅考虑q-s/2≤s-1 的情形. 由(q-1)s/2-(s/2-1)q=q-s/2及引理6之(iii)可知此情形下点s+1与点v到达点n-q+1的最短相同途径长为(q-1)s/2+n-s. 情形2: 若s为奇数. 此时按q的奇偶性可分2种情形讨论. 子情形2.1: 若s是奇数,q是偶数.设q/2=gs+r,其中g,r为非负整数且0≤r≤s-1. 再由g.c.d.(q,s)=1知1≤r≤s-1. 子情形2.1.2.1:若p(v,n-q+1)=n-s+r.此时p(v,n-q+1)-p(s+1,n-q+1)=r,再由(q/2-g)s-(s-1)q/2=r及引理6之(iii)可知此情形下点s+1与点v到点n-q+1的最短相同途径长为(s-1)q/2+n-s+r. 子情形2.1.2.2: 若p(v,n-q+1)=n-q+r. 子情形2.1.2.2.1:若g=0. 此时1≤q/2=r≤s-1,1≤p(v,n-q+1)-p(s+1,n-q+1)=s-q+r=s-q/2 子情形2.1.2.2.2:若g≥1.此时p(s+1,n-q+1)-p(v,n-q+1)=r+(2g-1)s,且有(q/2-g)s-(s-1)q/2=r成立,则由引理6之(ii)可知此情形下点s+1与点v到点n-q+1的最短相同途径长为(s-1)q/2+n-s. 情形2.2: 若s是奇数,q是奇数.设(q-s)/2=gs+r,其中g,r为非负整数,且0≤r≤s-1. 再由g.c.d.(q,s)=1知1≤r≤s-1.此时类似于子情形2.1的证明. 综上可知结论成立. □ 定理1 k(Dn,q,s)=min{⎣q/2」s,⎣s/2」q}+n-s= 注意到文献[1]定义的极图Ds,n为本文的图Dn,n,s,文献[12]定义的图Hn、图Qn和图Wn分别为本文的图Dn,n-1,n-2、图Dn,n-2,n-3和图Dn,n-1,n-3(这里n为偶数),所以文献[1]中定理3.10及文献[12]中引理3.10~引理3.12等结论均可为定理1的推论. 注意到若D是n阶本原有向图,其本原指数exp(D)与scrambling指数k(D)之间似乎存在某些内在的紧密联系,例如由文献[18]知其上界满足exp(D)≤(n-1)2+1,由文献[1]、[4]知k(D)≤「((n-1)2+1)/2⎤.下面再来看一些具体的图类. 由文献[10],若D是n阶本原对称矩阵的伴随有向图,其本原指数与scrambling指数满足k(D)=「exp(D)/2⎤. 由文献[20],若D=Dn,q,s是本原有向图,其本原指数exp(D)=sq+n-2s,再由定理1知 由文献[18],若D是恰含d个环的n阶本原有向图,其本原指数exp(D)≤2n-d+1,而由文献[7]、[12],其scrambling指数k(D)≤n-「d/2⎤. 由文献[18],若D是n阶完全不可分阵的伴随有向图,其本原指数exp(D)≤n-1,而由文献[12],其scrambling指数k(D)≤「(n-1)/2⎤. 由文献[18],若D是n阶本原几乎可约阵的伴随有向图,其本原指数exp(D)≤n2-4n+6,由文献[5]、[12],其scrambling指数k(D)≤「(n2-4n+7)/2⎤. 因此有 [1] AKELBEK M,KIRKLAND S. Coefficients of ergodicity and the scrambling index[J]. Linear Algebra Appl,2009,430: 1111-1130. [2] PAZ A. Introduction to probabilistic automata[M]. New York,London:Academic Press,1971. [3] CHO H H,KIM H K. Competition indices of digraphs[C]∥Proceedings of Workshop in Combinatorices,2004: 99-107. [4] SCHWARZ S. Common consequents in directed graphs[J]. Czechoslovak Math J,1985,35(2): 212-247. [5] ZHOU B. On the common consequent indices of nearly reducible binary relations[J]. Util Math,1999,56: 233-243. [6] ZHOU B,LIU B L. New results on the common consequent index of a binary relation[J].European J Combin,2000,21(2): 167-179. [7] MA H P,MIAO ZH K. On the set of common consequent indices of a class of binary relations[J]. Journal of Mathematical Research and Exposition,2008,28(3):460-468. [8] AKELBEK M,KIRKLAND S. Primitive digraphs with the largest scrambling index[J]. Linear Algebra Appl,2009,430: 1099-1110. [9] AKELBEK M,FITAL S,SHEN J. A bound on the scrambling index of a primitive matrix using Boolean rank[J].Linear Algebra Appl,2009,431: 1923-1931. [10] CHEN S X,LIU B L. The scrambling index of symmetric primitive matrices[J]. Linear Algebra Appl,2010,433:1110-1126. [11] KIM H K. Generalized competition index of a primitive digraph[J]. Linear Algebra Appl,2010,433: 72-79. [12] LIU B L,HUANG Y F. The scrambling index of primitive digraphs[J]. Comput Math Appl,2010,60: 706-721. [13] LIU B L,HUANG Y F. Generalized scrambling indices of a primitive digraph[J]. Linear Algebra Appl,2010,433: 1798-1808. [14] SIM M S,KIM H K. On generalized competition index of a primitive tournament[J]. Discrete Math, 2011,311: 168-182. [15] KIM H K,LEE S H. Generalized competition indices of symmetric primitive digraphs[J].Discrete Appl Math,2012,160: 1583-1590. [16] KIM H K,PARK S G. A bound of generalized competition index of a primitive digraph[J]. Linear Algebra Appl,2012,436: 86-98. [17] SHEN J. On a problem of Lewin[J]. Linear Algebra Appl,1998,274: 411-426. [18] LIU B L,LAI H J. Matrices in combinatorics and graph theory[M]. Dordrecht:Kluwer Academic Publishers,2000. [19] ROSS J A. On the exponent of a primitive nearly reducible matrix[J]. SIAM J Alg Discrete Math,1982,3: 395-410. [20] 吴钰涵,尤利华. 一类重要的本原(带号)有向图的指数值[J]. 华南师范大学学报:自然科学版,2011(3): 44-48. Keywords: primitive digraph; scrambling index; gaps; index set TheScramblingIndexofPrimitiveDigraphsDn,q,s YOU Lihua*, CHEN Fang (School of Mathematical Sciences,South China Normal University,Guangzhou 510631, China) 2012-07-03 国家自然科学基金项目(10901061,11071088);广州市珠江科技新星专项资助项目(2011J2200090) *通讯作者:尤利华,教授,Email: ylhua@scnu.edu.cn. 1000-5463(2013)05-0007-06 O151.21 A 10.6054/j.jscnun.2013.07.002 【中文责编:庄晓琼 英文责编:肖菁】









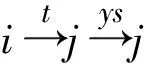
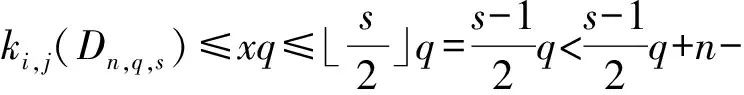
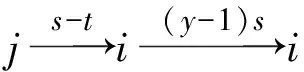
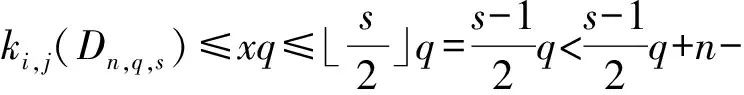
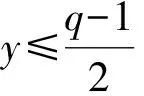
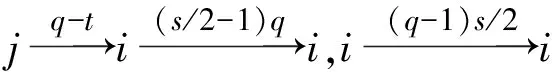
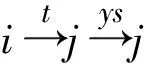
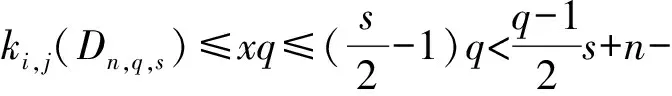
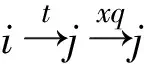
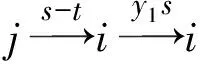
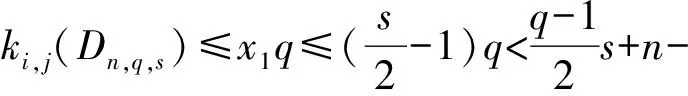
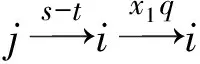

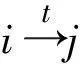
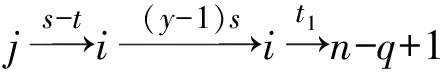
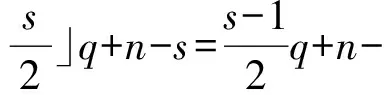
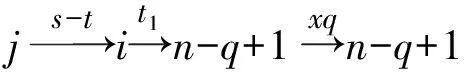
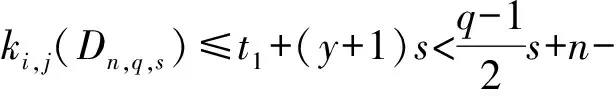
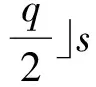
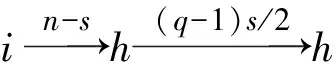

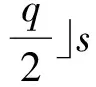

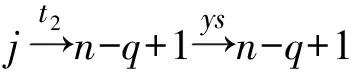
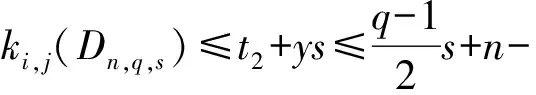
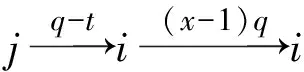
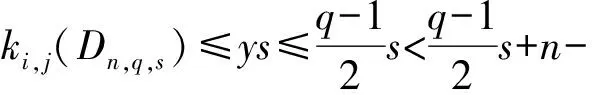
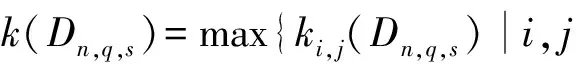



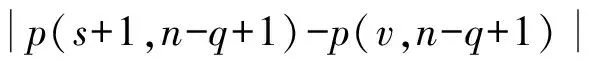

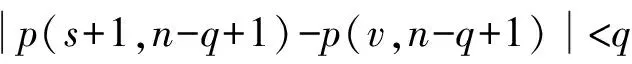

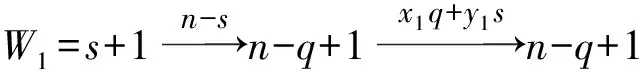
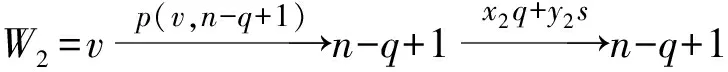
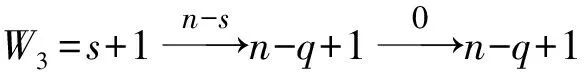
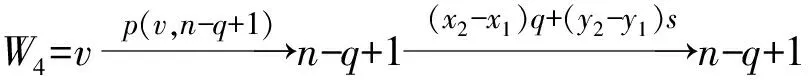
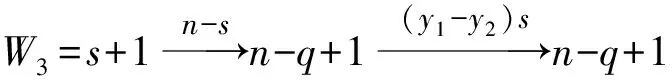
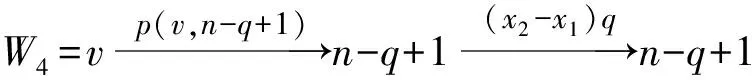
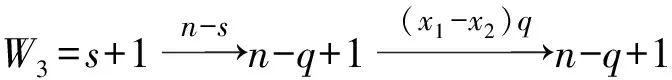
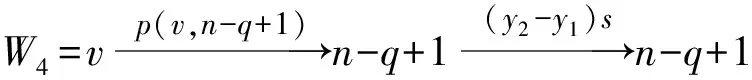




2 展望