一类四阶非线性抛物方程弱解的存在性

郭金勇

(柳州师范高等专科学校数学与计算机科学系，广西柳州545004)

非线性拟抛物方程是在物理、化学、经济问题和人口问题等大量实际问题中提出的一类重要的非线性发展方程，随着各个领域研究的需要，非线性拟抛物方程也得到了广泛研究和发展．文献［1］研究了一类具有非线性周期源的拟抛物方程

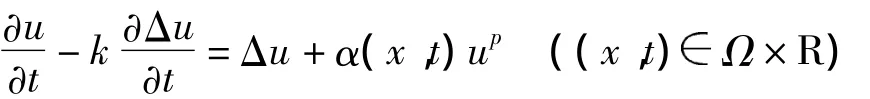
周期问题，依照非负非平凡周期解的存在和非存在性，给出了对指数p的完整分类．

关于非线性拟抛物方程整体解的存在性研究已取得许多结果．文献［2］研究了非线性拟抛物方程

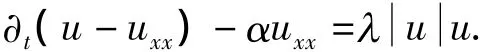
证明了初值问题整体解的存在性，讨论了解的渐近行为．

本文考虑如下四阶非线性抛物方程的初边值问题

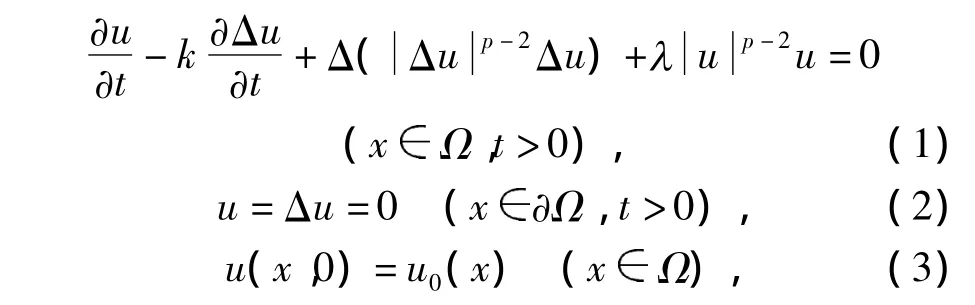
其中Ω⊂Rn为具有光滑边界的有界开区域，p＞2，λ＞0为参数，u0(x)为初始值函数，k＞0为粘性系数，表示粘性松弛因子或粘性，Δ2pu=称为p-双调和算子．

众多学者研究了具有p-双调和算子的椭圆方程并取得丰硕成果［3-4］，研究具p-双调和算子的抛物型方程的文献，并不多见．本文所研究的方程(1)为文献［1］和文献［2］研究的非线性拟抛物方程的变形，当k=0时，方程(1)变为具p-双调和算子的抛物型方程，其弱解的存在唯一性等结果可参阅文献［5］、［6］．由于退化，问题(1)～问题(3)不再有通常意义下的古典解，因此引入如下意义的弱解:

定义1 一个函数u被称为问题(1)～问题(3)的弱解，如果下列条件得到满足:

(1)u L∞(0，T;W2，p0(Ω))∩C(0，T;L2(Ω))，L∞(0，T;W-2，p'0(Ω))，其中p'是p的共轭指数．

(2)对φC∞0(QT)，QT=Ω×(0，T)，以下积分等式成立:

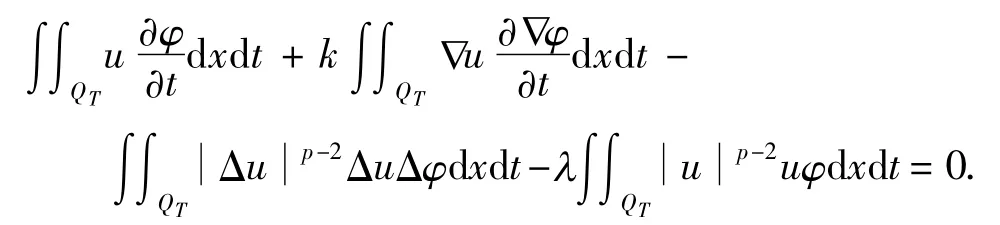
(3)在 L2(Ω)中，u(x，0)=u0(x)．

本文通过对时间的离散化构造并证明了逼近解的存在性，然后利用逼近解的一致估计结合紧致性原理证明了问题弱解的整体存在性．为叙述方便，假设k=λ=1，当k≠1及λ≠1时，证明方法相同．

1 主要结果及相关引理

本文的主要结果如下:

定理1 设 u0W2，p0(Ω)，p＞2，则问题(1)～问题(3)至少存在一个弱解．

为证明定理1，首先进行时间离散化．设N为正整数，把区间(0，T)分为N等分，取h=T/N(＞0)，考虑如下椭圆问题

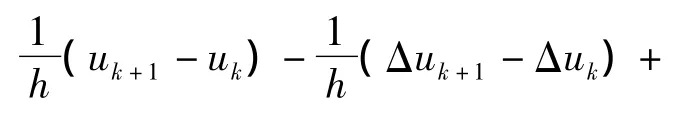
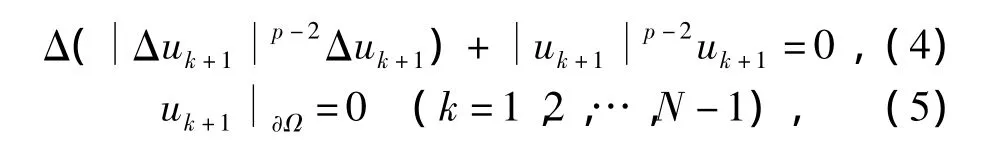
其中u0是初始值函数．

引理1 对固定的 k，若 ukW2，p0(Ω)，则存在uk+1W2，p0(Ω)，使得对任意的φC∞0(Ω)，有

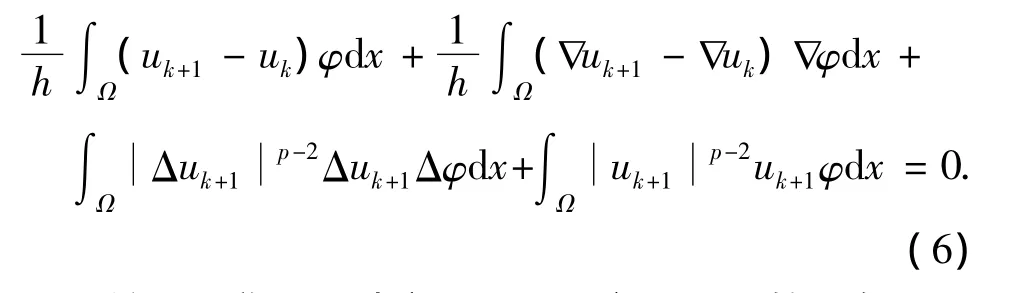
注1 称uk+1为问题(4)～问题(5)的弱解．

证明 在空间W2，p0(Ω)上，考虑泛函

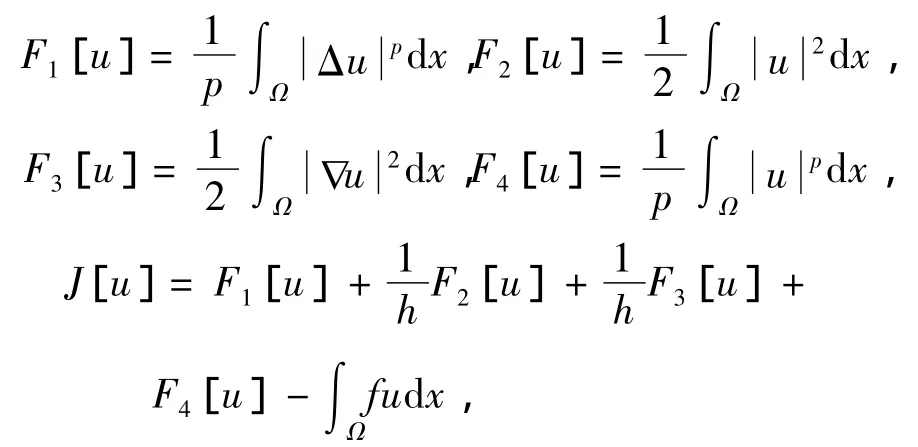
其中f L2(Ω)为已知函数．由Young不等式知，存在常数C1＞0使得

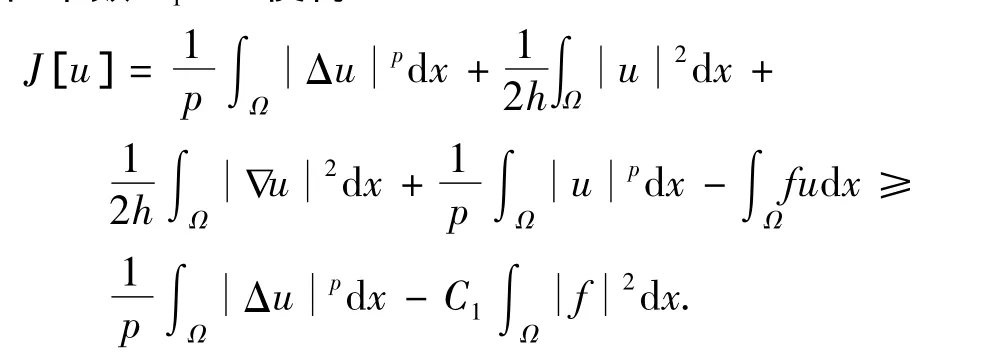
因为 J［u］在 W2，p0(Ω)上是弱下半连续的且满足强制性条件，根据文献［8］得出结论，存在u*(Ω)，使得 J［u*］=inf J［u］，且 u*为对应于J［u］的 Euler方程的弱解，取f=(uk-Δuk)，得到式(6)．证毕．

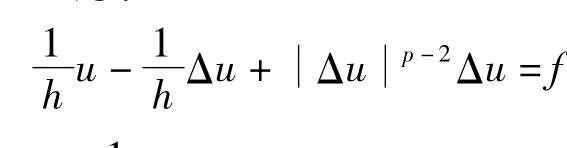
注2 容易证明对 φ W2，p0(Ω)，式(6)也成立．

现在，由如下式子

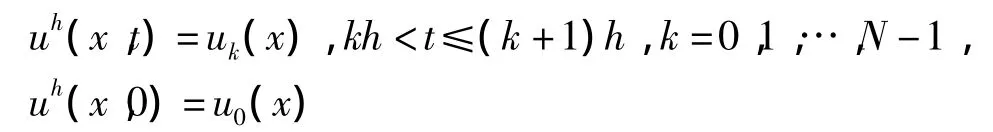
来构造问题(1)～问题(3)的逼近解，而问题(1)～问题(3)所描述的解将由{uh}的某个子序列的极限获得．为此，需要一些关于{uh}的一致性估计．

引理2 问题(4)、(5)的弱解uk满足

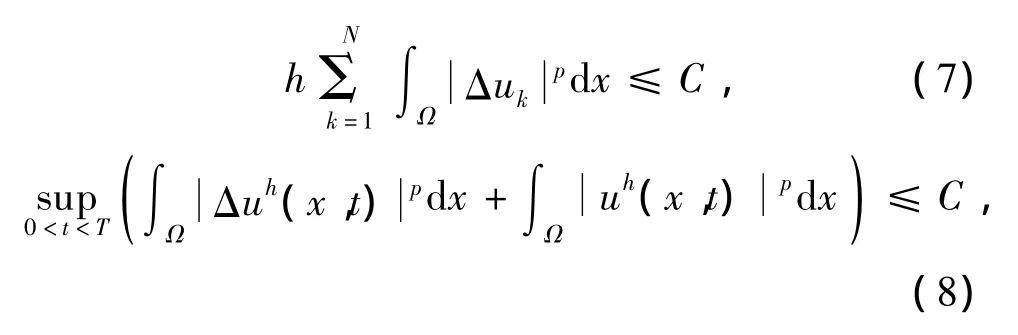
其中C是不依赖于h和k的常数．

证明 (i)在式(6)中取 φ=uk+1，应用 Young不等式并整理，得

把上式关于k从0到N-1相加，则有

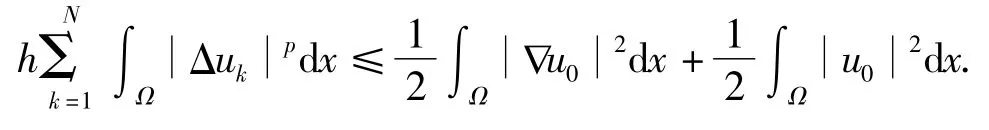
因此，式(7)成立．

(ii)在式(6)中取 φ=uk+1-uk，有

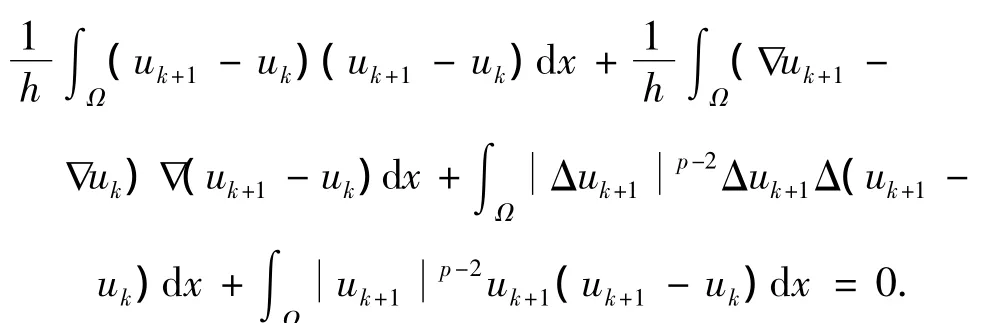
由于上式第一项和第二项非负，应用Young不等式，得

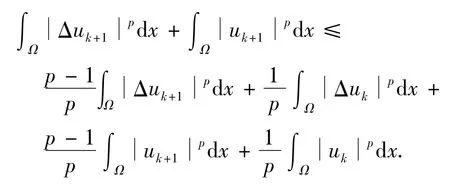
对任意的m(1≤m≤N-1)，上面不等式关于k从0到m-1相加，有

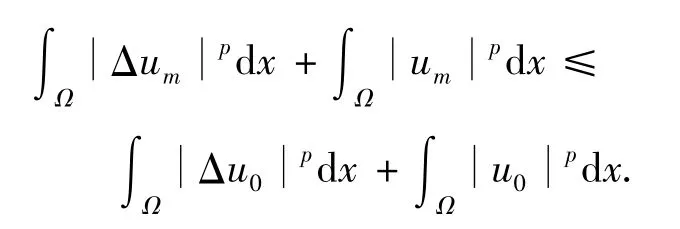
因此，式(8)成立．证毕．

引理3 对问题(4)、(5)的弱解uk+1，有估计式成立，其中C是不依赖于h的常数．

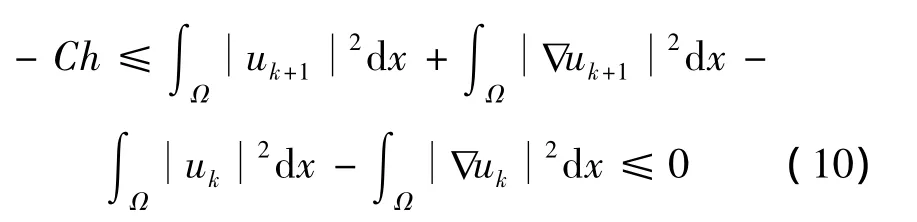
证明 右边的不等式由式(9)直接得到，只需证明左边的不等式．在式(6)中取φ=uk，由分部积分并使用边值条件，得

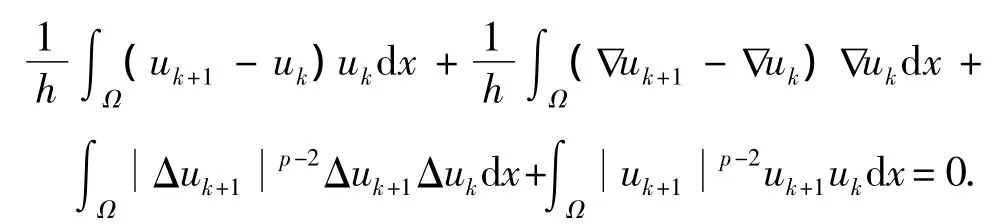
对上式应用Hölder不等式，并由式(8)得

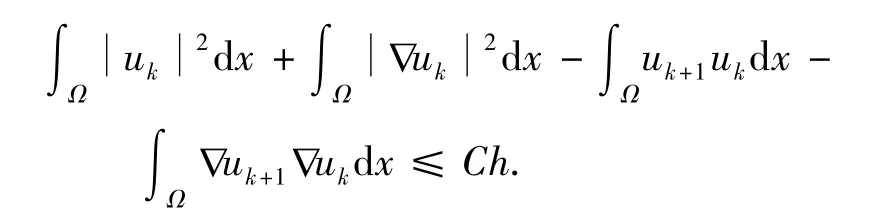
应用Young不等式，从上式推出式

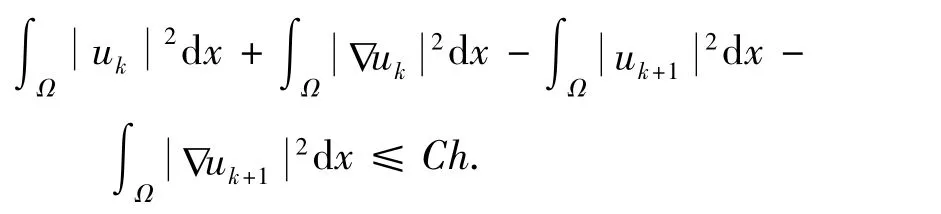
证毕．

2 主要结果的证明

定理1的证明 首先，定义算子At:At(Δuh)=p-2Δuk，Δhuh=uk+1-uk，其中 kh ＜t≤(k+1)h，k=0，1，…，N-1．由式(4)、(7)知Δhuh在 L∞(0，T;(W2，p(Ω))')中有界．再由式(6)、(8)，并使用文献［9］中的紧性结果，可知存在{uh}的一个子序列(不妨仍用原来的序列表示)，满足uh→u，弱* 于 L∞(0，T;W2，p(Ω))，uh→u，于 C(0，T;L2(Ω))，∇uh→∇u，弱* 于 L∞(0，T;L2(Ω))，(uk+1-uk)→，弱* 于 L∞(0，T;(W2，p(Ω))')，

At(Δuh)→w，弱* 于 L∞(0，T;Lp'(Ω))，其中p'为p共轭指数．由式(6)看出，对任意的φC0∞(QT)，有

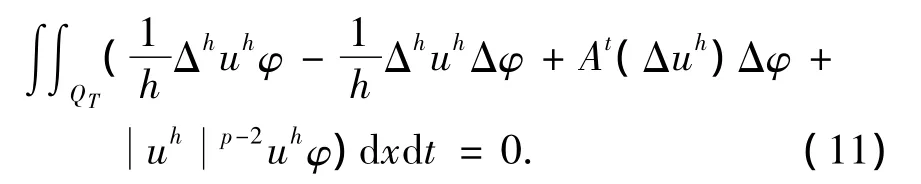
令h→0，在广义函数的意义下，由式(11)得

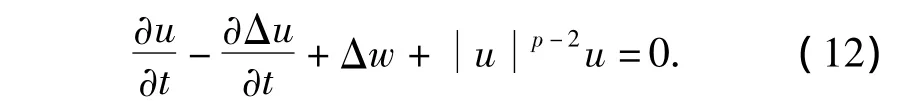
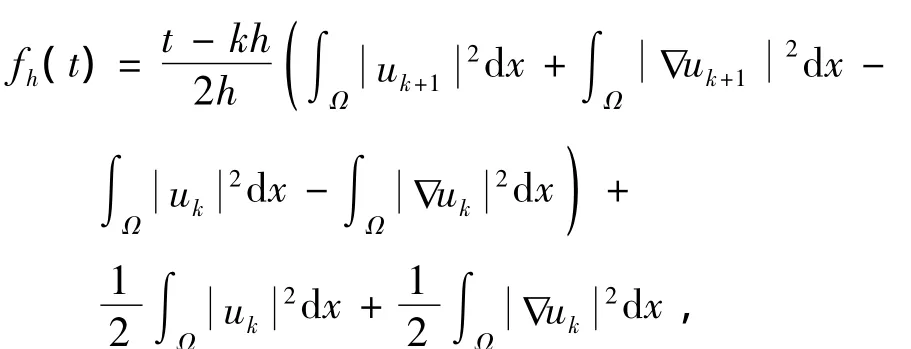
其中 kh＜t≤(k+1)h．由式(10)，有

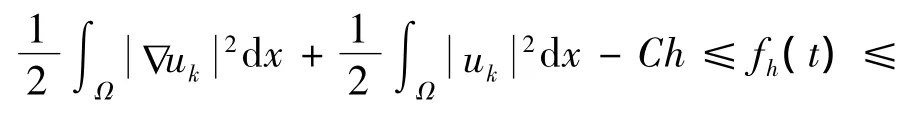
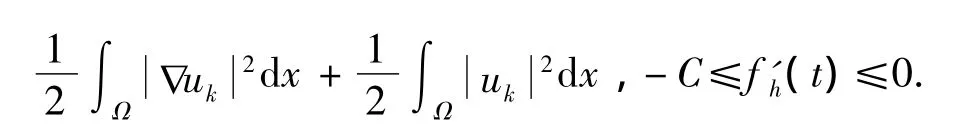
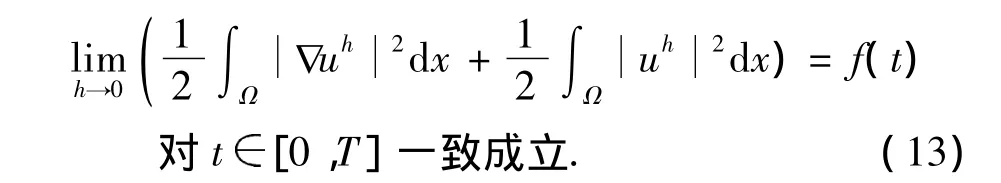
由式(9)，得

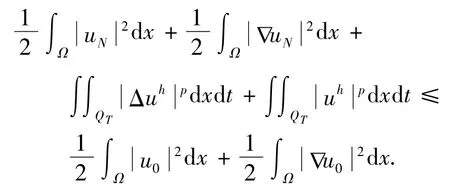
在上式中令h→0，并利用式(13)，得

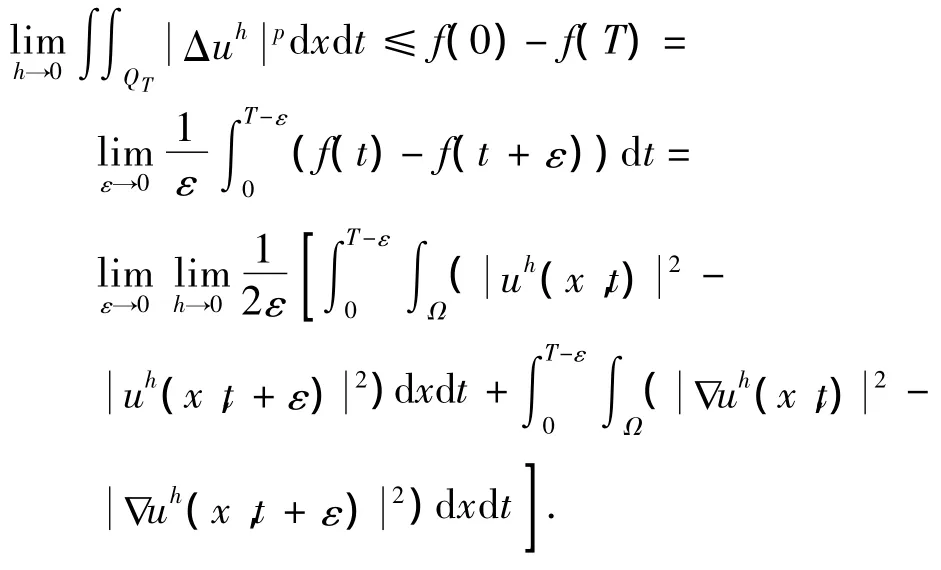
由于泛函

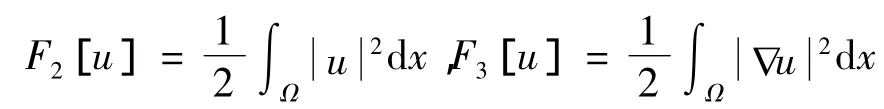
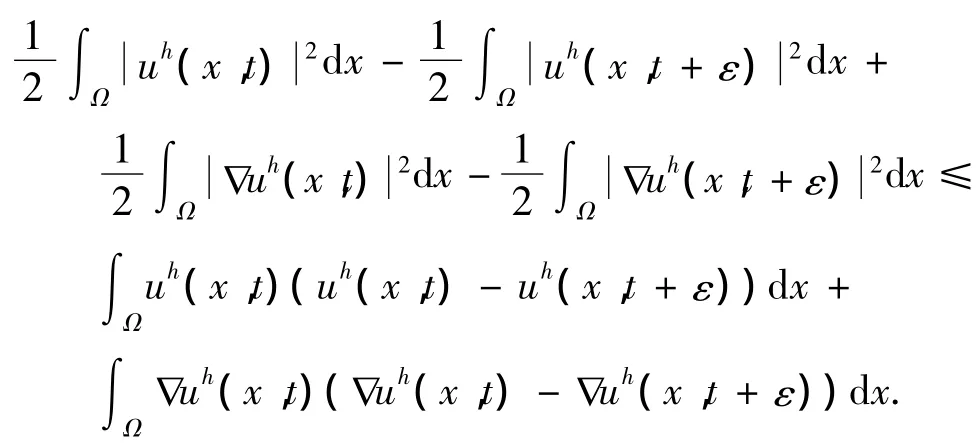
因此

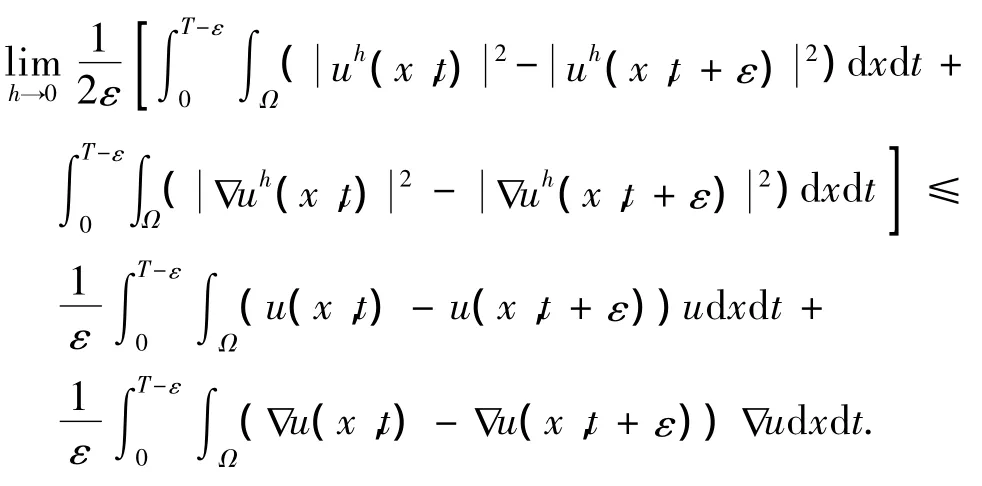
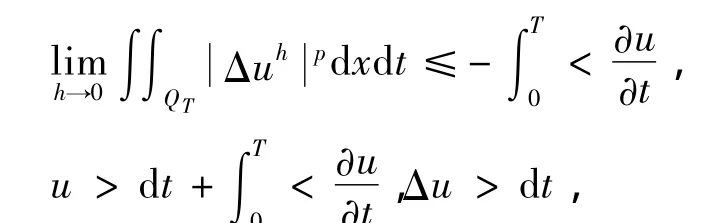
从而得到其中＜·，·＞表示内积．由式(12)，得

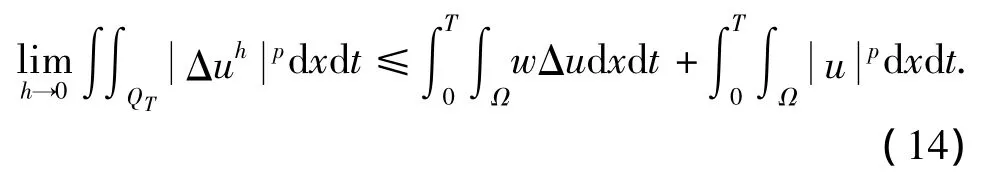
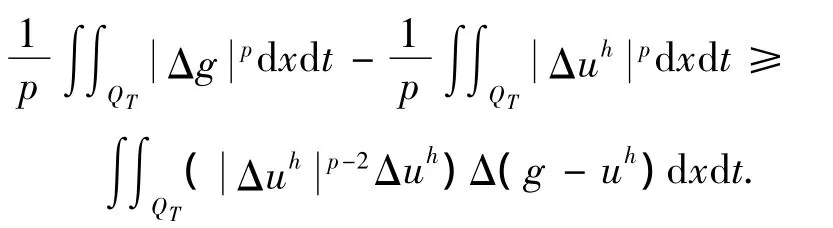
由式(14)和F1［u］是弱下半连续的，在上面不等式中令h→0并取极限，得

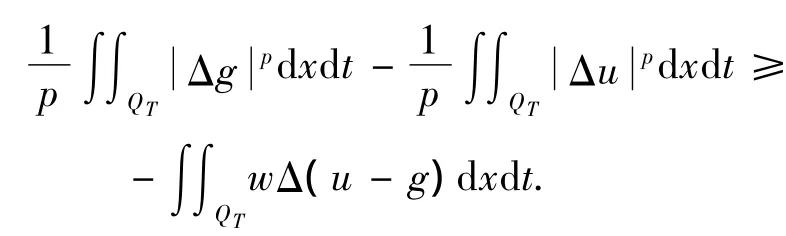
用εg+u代替上式的g，得

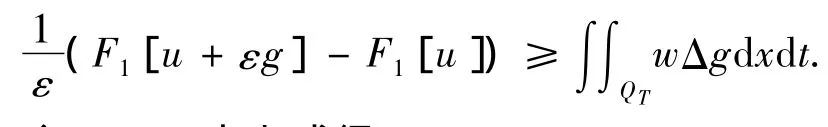
令ε→0，由上式得

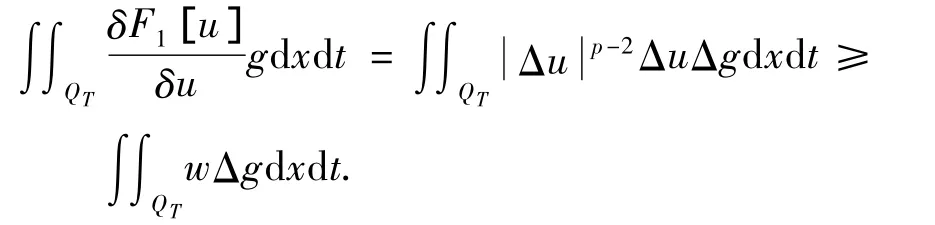
由g的任意性，取g=-g，得到上面不等式的反向不等式，所以w=Δu．由 uh在 C(0，T;L2(Ω))中强收敛且u(x，0)=u0(x)，得知u满足初值条件．证毕．

致谢 作者衷心感谢吉林大学数学学院刘长春教授的指导!

［1］CAO Y，YIN J X，JIN C H．A periodic problem of a semilinear pseudo parabolic equation［J］．Hindawi Publishing Corporation Abstract and Applied Analysis，2011:Art363579，27pp．

［2］ELENA IK．Initial-boundary value problem for nonlinear pseudo parabolic equations in a critical case［J］．Electronic JDE，2007(109):1-25．

［3］耿堤，田继青，邢小青．含临界非线性项的p-双调和方程正解的存在性［J］．华南师范大学学报:自然科学版，2004(4):23-28．

［4］郭慧敏，耿堤．类p-双调和方程Dirichlet问题无穷多解的存在性［J］．华南师范大学学报:自然科学版，2009(1):18-21;28．

［5］LIU CC，GUO JY．Weak solutions for a fourth order degenerate parabolic equation［J］．Bull Pol Acad Sci Math，2006，54(1):27-39．

［6］郭金勇．一个退化四阶抛物方程弱解的惟一性［J］．广西科学，2007，14(2):117-119．

［7］陈亚淅，吴兰成．二阶椭圆型方程与椭圆型方程组［M］．北京:科学出版社，1991．

［8］张恭庆．临界点理论及其应用［M］．上海:上海科学技术出版社，1986．

［9］SIMON J．Compact sets in the space Lp(0，T;Β)［J］．Ann Math Pura Appl，1987，146:65-96．