二阶线性周期微分方程的解和小函数的关系

袁舒婷，陈宗煊

(华南师范大学数学科学学院，广东广州510631)

1 引言与结果

本文使用值分布理论的标准记号［1-4］，并用λ(f)、(f)、σ(f)和 σ2(f)分别表示亚纯函数f(z)的零点收敛指数、不同零点序列的收敛指数、增长级以及超级，deg P表示多项式P(z)的次数．另外还使用(f-φ)表示亚纯函数f取小函数φ的点的收敛指数．陈宗煊［5］研究了4种类型的整函数系数的二阶线性微分方程的解的不动点及超级问题．GUNDEREN 和 STINBART［6］、陈宗煊［7］研究了关于二阶线性周期微分方程的次正规解的存在性、形式以及该方程所有解的增长性．

陈宗煊［7］证明了:

定理A 假设Pj(z)和Qj(z)(j=1，2)是z的多项式．如果 deg Q1≠deg P1，deg Q2≠deg P2，且 Q1+Q2≢0．那么方程

没有非平凡次正规解，且其每一个解满足σ2(f)=1．

定理B 假设Pj(z)、Qj(z)及Rj(z)(j=1，2)是z的多项式．如果 deg Q1≠deg P1，deg Q2≠deg P2，且Q1+Q2≢0，那么

(i)方程

最多有一个次正规解f0，且 f0具有形式

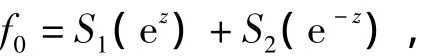
其中S1(ez)和S2(e-z)是z的多项式．

(ii)方程(2)的所有其他解f满足σ2(f)=1除去(i)中可能出现的次正规解．

定理A和定理B得出关于二阶线性周期微分方程的非次正规解的超级为1．文献［8］-［10］证明了在特定条件下，一些二阶线性微分方程的解以及它们的一阶导数、二阶导数、微分多项式取小函数的收敛指数都等于无穷．徐俊峰和仪洪勋［9］证明了:

定理C 假设Aj(z)(≢0;j=0，1)是整函数且σ(Aj)＜1，假设 a，b是复常数且满足ab≠0和a/b{1，2}，如果φ(≢0)是级小于1的整函数，那么方程

的每一个解f(≢0)满足

定理D 假设Aj(z)(≢0;j=0，1)是整函数且σ(Aj)＜1．假设 d0(z)，d1(z)，d2(z)是不全恒等于零的多项式，a，b是复常数且 ab≠0和 a/b {1，3/2，4/3，2，3，4}，φ(≢0)是级小于 1 的整函数．如果f(≢0)是方程(3)的一个整函数解，那么微分多项式 g(z)=d2f″+d1f'+d0f满足(g-φ)=∞．

对于方程(1)和方程(2)的解以及它们的一阶导数、二阶导数、微分多项式与小函数之间的关系将如何?这里得到如下结果:

定理1 假设Pj(z)和Qj(z)(j=1，2)是z的多项式．如果 deg Q1≠deg P1，deg Q2≠deg P2，且 Q1+Q2≢0．若设φ(z)(≢0)是级小于1的整函数，那么方程(1)的每个解f(≢0)满足(f-φ)=(f'-φ)=(f″-φ)=∞．

定理2 假设Pj(z)和Qj(z)(j=1，2)是z的多项式．如果 deg Q1≠deg P1，deg Q2≠deg P2，且 Q1+Q2≢0．设 d0(z)，d1(z)，d2(z)是不全恒等于零的多项式，φ(z)(≢0)是级小于1的整函数，如果f(≢0)是方程(1)的一个解，那么微分多项式g(z)=d2f″+d1f'+d0f满足(g-φ)=∞．

定理3 假设 Pj(z)，Qj(z)，Rj(z)(j=1，2)是 z的多项式．如果 deg Q1≠deg P1，deg Q2≠deg P2，且Q1+Q2≢0，R1+R2≠0．若设 φ(z)(≢0)是级小于 1的整函数且φ不为常数，那么方程(2)最多有一个次正规解f0，f0=S1(ez)+S2(e-z)，其他所有解满足(f-φ)=(f'-φ)=(f″-φ)=∞．

定理4 假设 Pj(z)，Qj(z)，Rj(z)(j=1，2)是 z的多项式．如果 deg Q1≠deg P1，deg Q2≠deg P2，且 Q1+Q2≢0，R1+R2≠0．设 d0(z)，d1(z)，d2(z)是不全恒等于零的多项式，φ(z)(≢0)是满足0＜σ(φ)＜1的整函数，如果f(z)是方程(2)的非次正规解，那么微分方程 g(z)=d2f″+d1f'+d0f满足(g-φ)=∞．

2 定理的证明

本文假设

其中 ajmj，…，aj0;bjnj，…，bj0;cjlj，…，cj0(j=1，2)是常数，mj≥1，nj≥0，lj≥0 是整数，ajmj≠0，bjnj≠0，cjlj≠0．

引理 1［11］假设 A，A，…，A，F≢0 为有穷

01k-1级亚纯函数，如果f(z)是方程的一个无穷级亚纯函数解，那么f满足(f)=λ(f)=σ(f)=∞．

引理2［8］假设 f是无穷级整函数，d(z)(j=j0，1，2)是不全恒为零的多项式．那么w(z)=d2f″+d1f'+d0f具有无穷级．

定理1的证明 假设f(≢0)是方程(1)的解，由定理A可知σ(f)=∞及σ2(f)=1．令 g0(z)=f(z)-φ(z)，那么σ(g0)=σ(f)=∞φ)．将f=g0+φ 代入方程(1)，得到

若 φ″+(P1+P2)φ'+(Q1+Q2)φ≡0，那么 φ为方程(1)的解，则σ(φ)=∞与φ的级小于1矛盾．故式(4)的右边≢0．由引理1可知，(g0)=σ(g0)=∞，即(f-φ)=∞．

下面证明λ(f'-φ)=∞，令 g1(z)=f'-φ，那么σ(g1)=σ(f')=σ(f)=∞对方程(1)两边进行微分得

由方程(1)，得到

把式(6)代入式(5)，得到

将 f'=g1+φ，f″=g'1+φ'，f‴=g″1+φ″代入式(7)，得到

其中

现证h≢0，只需证(Q1+Q2)h≢0，化简成

这里的M0以及后面出现的Mi(i=1，2，…，6)，Nj(j=0，1，2，3)都是不影响讨论的含 ez和 e-z的函数．

令deg Q1=n1，deg Q2=n2，deg P1=m1，deg P2=m2．由 deg Q1≠deg P1，deg Q2≠deg P2，可知 n1≠m1，n2≠m2．故可分成3种情况来讨论:

(i)当 n1＞m1时，取 z=r，则式(9)的左边中含e的最高次项在-Q1φ中，即含e1这一项，故

(ii)当 n2＞m2时，取 z=-r，则式(9)左边中含e-z的最高次项在-Q22φ中，即含e-2n2z这一项，故

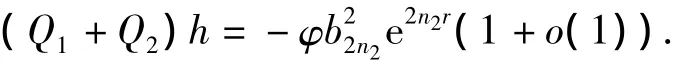
(iii)当 m1＞n1且 m2＞n2时，取 z=r，则式(9)左边中含 ez的最高次项在 -P1Q1φ'+(P1Q'1-P'1Q1)φ中，即找出含e(m1+n1)z的项，再合并它们的系数，故

如果 φ'/φ =n1-m1，那么 φ =c e(n1-m1)z(c≠0)．则 σ(φ)=1，与σ(φ)＜1矛盾．故由 φ'+(m1-n1)φ，a1m1，b1n1，b2n2都不恒为零，推出(Q1+Q2)h≢0．即 h≢0．

微分式(5)的两边，得到

由式(7)得到

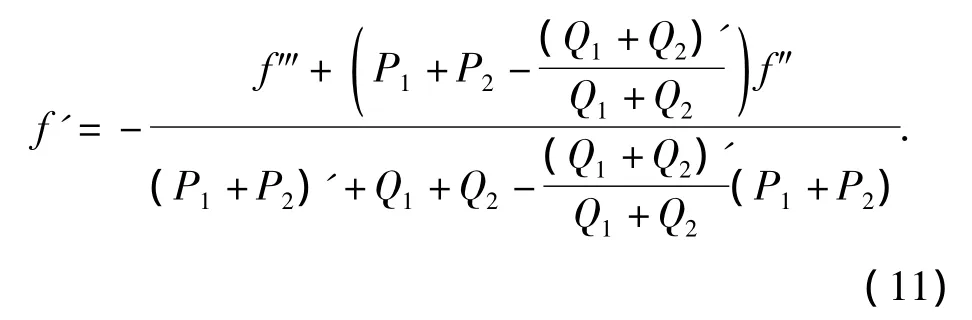
将式(6)、(11)代入式(10)得到

这里

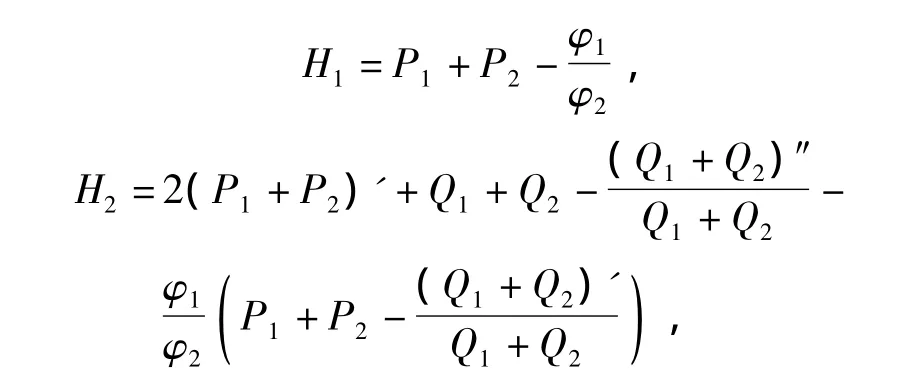
其中

(φ2≢0)，显然，H1，H2，φ1，φ2是亚纯函数且 σ(Hj)≤1(j=1，2)，σ(φk)≤1(k=1，2)．

将 f″=g2+ φ，f‴=g'2+ φ'，f(4)=g″2+ φ″代入式(12)，得到

令 H=-(φ″+H1φ'+H2φ)，化简

(i)当 n1＞m1时，取 z=r，则 φ2(Q1+Q2)H 中含φ的ez的最高次项在-Q31φ中，故

φ2(Q1+Q2)H=(1+o(1))．

(ii)当n2＞m2时，取z=-r，则φ2(Q1+Q2)H中含φ的e-z的最高次项在-Q32φ中，故

φ2(Q1+Q2)H=(1+o(1))．

(iii)当 m1＞n1且 m2＞n2时，取 z=r，则找出式(14)右边中含e(2m1+n1)z的项并合并它们的系数得φ2(Q1+Q2)H=(n1-m1)［φ'+(m1-n1)φ］×

由于 φ'+(m1-n1)φ，a1m1，b1n1，b2n2都不恒为零，推出φ2(Q1+Q2)H≢0．即 H≢0．

对式(12)来说，H≢0．由引理1知

定理2的证明 先设d2(z)≢0，假设f(≢0)是方程(1)的解，由定理A可知σ(f)=∞．令w=d2f″+d1f'+d0f-φ，由引理2可知 σ(w)=σ(g)=σ(f)=∞．为证，仅需证

将f″=-(P1+P2)f'-(Q1+Q2)f代入 w(z)中得到

对式(15)的两边微分且用 f″=-(P1+P2)f'-(Q1+Q2)f代入w(z)替换f″得到

则令

先判断 h≢0，根据 deg Q1≠deg P1，deg Q2≠deg P2，要分成3种情况讨论．

(i)当n1＞m1时，取 z=r，则h中含ez的最高次项在-d2Q21中，即找出含e2n1z的项，故

(ii)当n2＞m2时，取 z=-r，则 h中含 e-z的最高次项在-d2Q22中，即找出含e-2n2z的项，故

(iii)当 m1＞n1且 m2＞n2时，取 z=r，又要分 3种情况．

(a)当d0≢0时，则 h中含ez的最高次项在-d0d2P21中，即含e2m1z的项．故

(b)当 d0=0，d1≢(m1-n1)d2时，则 h中含 ez的最高次项在d22P1Q'1-d22P'1Q1+d1d2P1Q1中，即含e(n1+m1)z的项．故

(c)当 d0=0，d1=(m1-n1)d2时，则 h中含 ez的最高次项在-d2Q21中，即含e2n1z的项．故

综上可知h≢0，由式(17)得到

其中

微分式(24)的两边

将式(24)～(26)代入到方程(1)得到

其中Φ0和Φ1是级小于或等于1的不影响讨论的整函数且

这里

其中A1是不影响讨论的关于ez和e-z的函数．

现讨论F，α0h是否不恒等于零．

(i)当n1＞m1时，取 z=r，则 F 中含 ez的最高次项在-d2φQ21h这一项中，再结合式(19)．即找出含e4n1z的项，故

(ii)当 n2＞m2时，取 z=-r，即含 e-4n2z的项．故(1+o(1))(1+o(1))．

(iii)当m1＞n1且m2＞n2时，取z=r，观察F 中的ez的最高次数的项又要分3种情况．

(a)当 d0≢0时，由式(21)得

这里再分成2种情况:

(1)当 φ≢cd0时，将式(21)、(29)～(32)代入到式(28)找出含e(n1+3m1)z的项，合并它们的系数得

(2)当φ=cd0时，则 F中含 ez的最高次项在-d2φQ21h这一项中，再结合式(21)，有

(b)当d0=0，d1≢(m1-n1)d2时，由式(22)得

将式(22)、(29)～(31)和式(33)代入到式(28)找出含e2(n1+m1)z的项，合并它们的系数得到

其中(c≠0)，此时σ(φ)=1 与 σ(φ)＜1 矛盾．故A2≢0．(c)当 d0=0，d1=(m1-n1)d2时，由式(23)得

将式(23)、(29)～(31)和式(34)代入到式(28)，找出含e(3n1+m1)z的项合并它们的系数得到

这里若2(m1-n1)d2φ +d2φ'-d'2φ =0，则 φ =cd2e2(n1-m1)z(c≠0)，此时 σ(φ)=1，与 σ(φ)＜1矛盾．故2(m1-n1)d2φ +d2φ'-d'2φ≢0．综上可得

即对方程(27)，由引理2，σ(w)=∞和式(35)，可得(w)=σ(w)=∞．

下面假设 d2≡0，d1≢0，d0≢0．使用类似于上面的证法，能得到(w)=σ(w)=∞．

最后如果 d2≡0，d1≢0，d0≡0 或 d2≡0，d1≡0，d0≢0，那么对w=djf(j)-φ(j=1或0)，可以考虑w/dj=f(j)-φ/dj．由于(w)=(w/dj)(dj是多项式)．类似于定理1的证明和 σ(w)=∞，可得(w)=σ(w)=∞．

定理3的证明 设f是方程(2)的非次正规解，由定理B可知σ(f)=∞．类似定理1的证明得到(f-φ)=∞．

其中h1，h2和定理1中的相同，

化简

对于式(37)，因为φ不为常数，同理分析得(Q1+Q2)h3≢0．即

化简

因为φ不为常数且σ(φ)＜1，所以φ≢R1+R2．同样分析可得φ2(Q1+Q2)H3≢0．即

定理4的证明 先设d2(z)≢0，假设f是方程(2)的非次正规解，由定理B知σ(f)=∞．同样用定理2方法得到

这里的 α0，h，Φ1，Φ0和定理 2 中的相同而

其中

对于F1中的

此时当φ=d2(R1+R2)时，R1+R2可分成2种情况:

(1)若 R1+R2=c，则σ(φ)=σ(d2c)=0;

(2)若R1+R2≠c，则σ(φ)=σ(d2(R1+R2))=1．

但这2种情况与0＜σ(φ)＜1矛盾．故下面仅讨论φ≠d2(R1+R2)．

(i)当n1＞m1时，取 z=r，则 F1中含 φ 的 ez的最高次项在-d2(Q1+Q2)2［φ-d2(R1+R2)］h中，再结合式(19)找出含e4n1z的项．故

(ii)当 n2＞m2时，取 z=-r，即找出含 e-4n2z的项．故

(iii)当 m1＞n1且 m2＞n2时，取 z=r，观察 F1中的ez的最高次数的项又要分3种情况:

(a)当d0≢0时，仅需讨论F1中d0d2P21R1h含ez的最高次数的项，再结合式(21)找出含e(l1+4n1)z的项．故F1=

(b)当 d0≡0，由式(42)得

把式(43)～(45)代入F1得

若d1≢(m1-n1)d2，结合式(22)找出式(46)含e(l1+2n1+2m1)z的项再合并它们的系数得到

若d1≡(m1-n1)d2，仅需讨论式(46)中d22R1Q21h含ez的最高次项，再结合式(23)找出含e(l1+4n1)z的项．故

综上讨论可知 F1≢0，α0h≢0．且由引理2，σ(w)=∞得到

［1］HAYMAN W K．Meromorphic functions［M］．Oxford:Clarendon Press，1964．

［2］杨乐．值分布论及其新研究［M］．北京:科学出版社，1982．

［3］仪洪勋，杨重骏．亚纯函数的唯一性理论［M］．北京:科学出版社，1995．

［4］LAINE I．Nevanlinna theory and complex differential equations［M］．Berlin:Wde Gruyter，1993．

［5］陈宗煊，二阶复域微分方程解的不动点与超级［J］．数学物理学报，2000，20(3):425-432．

［6］GUNDEREN G，STINBART M．Subnormal solutions of second order linear differential equations with periodic coefficients［J］．Results in Math，1994，25:270-289．

［7］陈宗煊．关于二阶线性周期微分方程的次正规解［J］．中国科学:A，2007，37(3):361-374．

［8］陈宗煊，孙光镐．一类二阶微分方程的解和小函数的关系［J］．数学年刊，2006，A27:431-442．

［9］徐峻峰，仪洪勋．微分方程的解和小函数的关系［J］．数学学报，2010，53(2):291-296．

［10］安蕾，肖丽鹏．一类2阶微分方程的解和小函数的关系［J］．江西师范大学学报:自然科学版，2013，37(3):233-235．

［11］CHEN Zongxuan．Zeros of meromorphic solutions of higher order linear differential equations［J］．Analysis，1994，14:425-438．