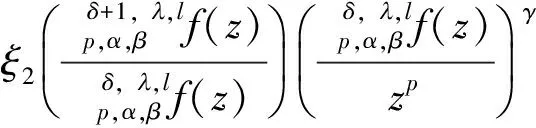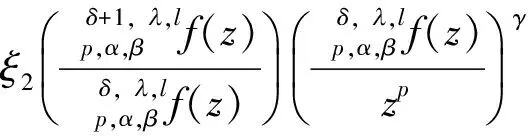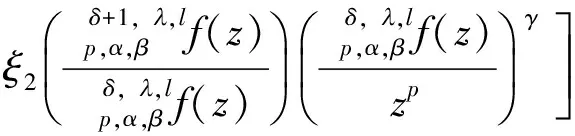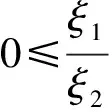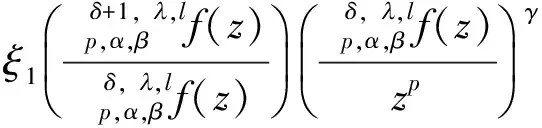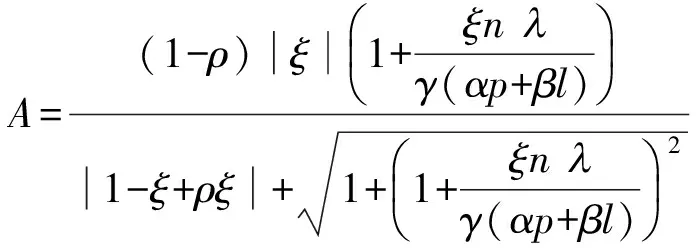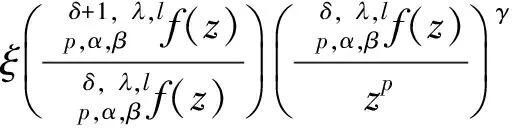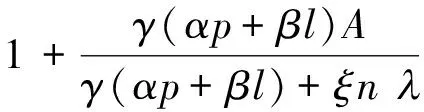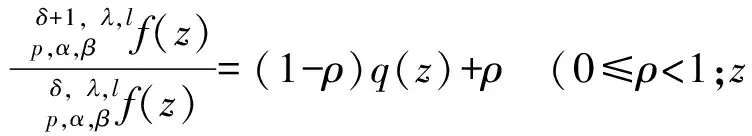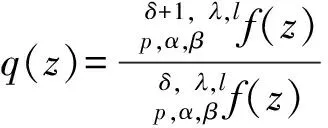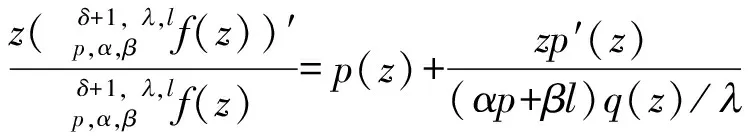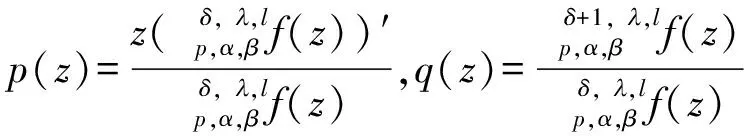用算子δ, ,lp,α,β定义的多叶解析函数子类的性质
2013-10-27高松云刘名生
高松云, 刘名生
(华南师范大学数学科学学院, 广东广州 510631)
高松云, 刘名生*
(华南师范大学数学科学学院, 广东广州 510631)
利用算子δ,,lp,α,βf(z)的性质研究了多叶解析函数子类δ,,l,ξ,Ap,α,β,γ,B的一些性质,得到子类δ,,l,ξ,Ap,α,β,γ,B的充分条件、从属关系、包含关系、卷积性质和不等式性质.
多叶解析函数; 微分从属; Hadamard乘积或者卷积
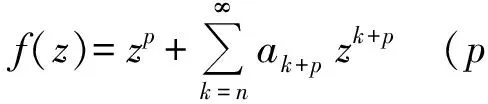
(1)
的函数f所成的函数类. 如果f由式(1)定义,g定义如下
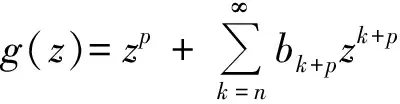
(2)
那么f和g的卷积定义为:
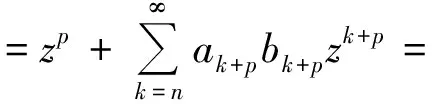
令f(z)和g(z)在单位圆盘U内解析.称f(z)从属于g(z),记作在U上f(z)g(z)或f(z)g(z) (zU),如果存在解析函数w(z)且满足在zU上有以及f(z)=g(w(z))成立.
2007年,SRIVASTAVA和ATTIYA[1]提出算子:
(,

2010年,CHO等[2]推广了Srivastava-Attiya算子:
(,

2007年,CATAS[3]提出算子:
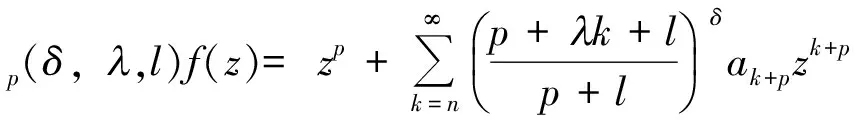



其中的幂函数取主值,下面应用这一约定.
显然,当α=β=1,δ,,l≥0时,δ,v,lp,α,βf(z)退化为Catas算子;当p=α=β==1时,δ,,lp,α,βf(z)退化为Srivastava-Attiya算子;当α=β==1时,δ,,lp,α,βf(z)退化为CHO等[2]推广的Srivastava-Attiya算子.

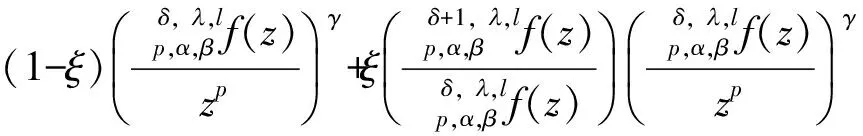
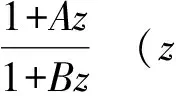
(3)

先给出证明本文的主要结果需用到的引理.
引理1[6]设函数h(z)在单位圆盘U内单叶解析且h(0)=1,k(z)在单位圆盘解析且有如下的定义方式
k(z)=1+cnzn+cn+1zn+1+…
如果
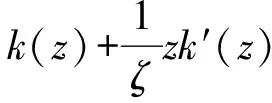
(4)
那么
k(z)h(z),
引理2[7]设函数φ(z)是U内的凸函数,且h(0)=1,(βφ(z)+γ)>0.如果函数p(z),q(z)满足以下的微分从属关系:
q(z)φ(z),
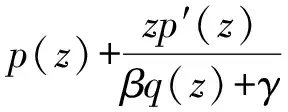
那么p(z)φ(z)(zU).

f(z)+(1-)g(z)F(z) (0≤≤1).

p(z)=1+anzn+an+1zn+1+…
和
p(z),
这里
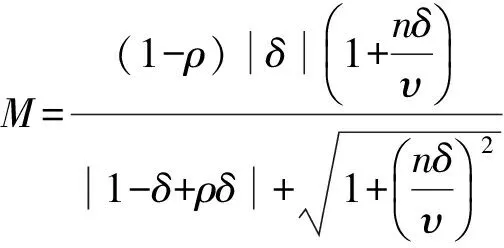
如果q(z)在U内解析,且与p(z)具有同样形式的Taylor展开式,并满足
p(z)[1-δ+δ((1-ρ)q(z)+ρ)]1+Mz,
下面给出本文的主要结果及其证明.

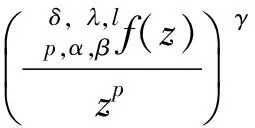

(5)
证明定义函数P(z)如下:
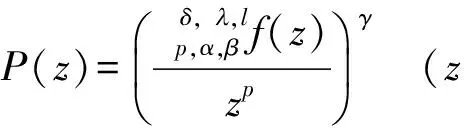
(6)
则P(z)在单位圆盘U内解析且P(0)=1. 对式(6)两边求对数导数得
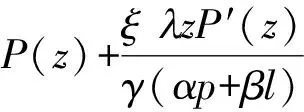
(7)
根据引理1,得
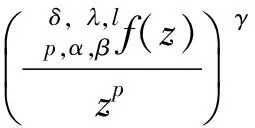

注1 当α+βl==p=1时,由定理1可得到文献[10]中的定理1.

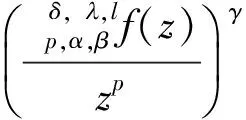
(8)
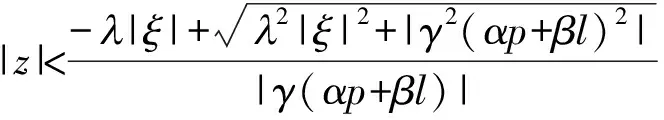
证明由式(8),可设
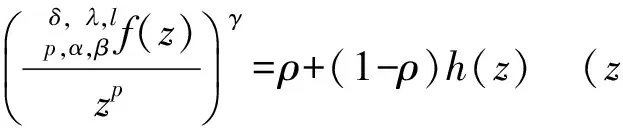
(9)
这里h(z)是U内的正实部函数. 对式(9)两边求对数导数,得到
(1-ρ)
(1-ρ),
(10)
应用几何函数论中的基本定理得
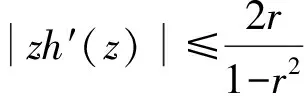
由式(10)可以得到
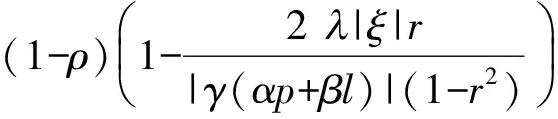
(11)
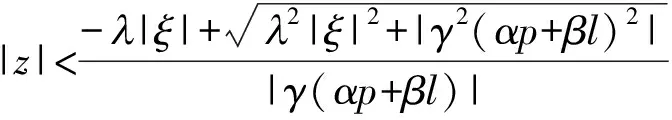
□

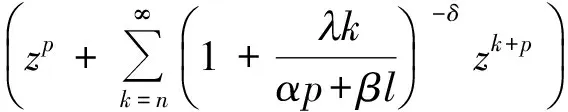
(12)
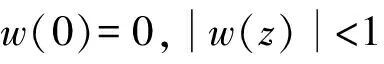

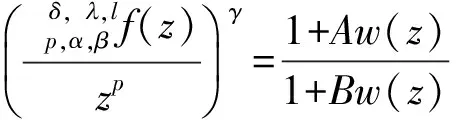
(13)
其中w(z)在U内解析,且w(0)=0,|w(z)|<1. 由上式和定义1易得
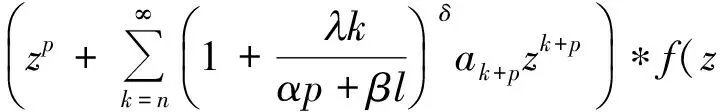
(14)
所以得到式(12),证毕.
□
定理4 设ξ2≥ξ1≥0,-1≤B1≤B2 δ,,l,ξ2,A2p,α,β,γ,B2⊂δ,,l,ξ1,A1p,α,β,γ,B1. (15) 因为-1≤B1≤B2 (16) 由定理1和式(16),可得 (17) 同时 (18) □ 注2 当α+βl==p=1时,由定理4 可得到文献[10]中的定理3. 最后导出一个不等式性质和星像函数的一个充分条件. 那么 . (19) 函数P(z)定义如式(6),由定理1,得 P(z) 令 则式(19)可以化简为 P(z){(1-ξ)+ξ[(1-ρ)q(z)+ρ]}1+Az(zU). (20) (21) 由 (22) 得到 . □ δ,,lp,α,βf(z)S*. 证明因为δ+1,,lp,α,βf(z)S*,可得 . 由式(22)得 其中 . □ [1] SRIVASTAVA H M,ATTIYA A A. An intergral operator associated with the Hurwitz-lerch zeta function and differential subordination[J]. Intergral Transforms Spec Funct, 2007, 18:207-216. [2] CHO N E, KIM I C, SRIVASTAVA H M. Sandwich-type theorems for multivalent functions associated with the Srivatava-Attiya Operator[J]. Applied Mathematics and Computation, 2010, 217: 918-928. [3] CATAS A. On certain classes of p-valent functions defined by multiplier transfor[C]∥International Symposium on Gemetry Function Theory and Applications, Istanbul, 2007. [4] CATAS A,OROS G I,OROS G. Differential subordinations associated with multiplier transformation[J]. Abst Appl Anal, 2008: Art 845724, 11pp. [5] CATAS A.Neighborhoods of certain class of analytic functions with negative coefficients[J]. Banach J Math Anal, 2009(3):111-121. [6] MILLER S S,MOCANU P T. Differential subordination:Theory and applications[M]. New York, Basel: Marcel Dekker Incorporated, 2000. [7] PADMANABHAN K S,PARVATHAM R. Some applications of differential subordination[J]. Bull Austral Math Soc, 1985, 32: 321-330. [8] 刘名生. 关于某类解析函数[J]. 华南师范大学学报:自然科学版, 2002(4):15-20. [9] LIU Mingsheng. On the starlikeness for certain subclass of analytic functions and a problem of Ruscheweyh[J].数学进展, 2005, 34(4): 416-424. [10] LIU Mingsheng. On certain subclass of analytic functions defined by differential subordination[J]. Acta Math Scientia:Ser B, 2002, 22(3):388-392. Keywords:multivalentanalyticfunction;differentialsubordination;Hadamardproduct(orconvolution) PropertiesofSubclassofMultivalentAnalyticFunctionsDefinedbytheOperatorδ,,lp,α,β GAOSongyun,LIUMingsheng* (SchoolofMathematicalSciences,SouthChinaNormalUniversity,Guangzhou510631,China) Some properties for a certain subclassδ,,l,ξ,Ap,α,β,γ,Bofmultivalentfunctionsdefinedbythecertainoperatorδ,,lp,α,βf(z)areinvestigated.Suchresultsassufficientconditions,subordinationrelations,inclusionrelationships,convoltionpropertiesandinequalitypropertiesareproved. 2012-04-24 教育部博士点基金项目(20050574002) *通讯作者:刘名生,教授,Email: liumsh@scnu.edu.cn. 1000-5463(2013)05-0019-04 O174.51 A 10.6054/j.jscnun.2013.07.004 【中文责编:庄晓琼 英文责编:肖菁】