圆锥曲线中最值、范围、定值及存在性问题

2013-10-27虞金龙

中学教研(数学) 2013年3期

关键词：考试题定值抛物线

●虞金龙

(绍兴市第一中学浙江绍兴 312000)

圆锥曲线中最值、范围、定值及存在性问题

●虞金龙

(绍兴市第一中学浙江绍兴 312000)

1 考点回顾

圆锥曲线中最值、范围、定值及存在性问题是历年高考命题的热点之一.此类问题涉及的知识面广、综合性大、隐蔽性强、计算量大，常常令考生头疼.解决此类问题常常要用到数学思想方法，有时题设条件纷繁复杂，使得考生答题举步维艰.近几年的浙江省数学高考都考到圆锥曲线中最值、范围、定值及存在性问题，本文给出该类题型的一些解法，旨在抛砖引玉.

2 典题剖析

2.1 最值问题

解答圆锥曲线中最值问题的常用方法有：几何法、函数法、不等式法.几何法是根据图形几何性质求解的方法；函数法是指将所求变量表示成某个相关变量的函数，再求函数的最值；不等式法是根据曲线性质及条件建立一个关于所求变量的不等式，再解不等式求其最值的方法．

图1

(1)求椭圆C的方程;

(2)求△ABP的面积取最大时直线l的方程.

(2012年浙江省数学高考理科试题)

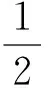
从而

3x2-3mx+m2-3=0.

显然Δ=(3m)2-4×3(m2-3)=3(12-m2)>0,

故

由韦达定理，得

又因为点P(2,1)到直线l的距离为

下面利用导数求解:令u(m)=(4-m)2(12-m2),则

u′(m)= -4(m-4)(m2-2m-6)=

评注本题是利用函数法求最值，特别是最后用导数求解，学生往往难以想到，有一定的难度.

2.2 范围问题

圆锥曲线中的范围问题，一般先根据条件列出所求目标的函数关系式，然后根据函数关系式的特征选用参数法、配方法、判别式法、不等式法、单调性法、导数法以及三角函数最值法等求出它的最大值和最小值，从而确定参数的范围.

图2

例2如图2,动点M与2个定点A(-1,0),B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C.

(1)求轨迹C的方程;

(2012年四川省数学高考试题)

分析(1)轨迹C的方程为

3x2-y2-3=0(x>1).

由题意,方程(1)有2个根且均在(1,+∞)内.设f(x)=x2-4mx+m2+3,则

解得

m>1且m≠2.

设点Q,R的坐标分别为(xQ,yQ),(xR,yR),由|PQ|<|PR|，得

由m>1且m≠2,得

2.3 定值问题

圆锥曲线中的定值问题包括几何量的定值或曲线系(直线系)过定点等问题，处理时可以直接推理求出定值，也可以先通过特定位置猜测结论后进行一般性证明.对于客观题，通过特殊值法探求定点、定值能达到事半功倍的效果．

例3在直角坐标系xOy中,曲线C1的点均在圆C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=-2的距离等于该点与圆C2上点的距离的最小值.

(1)求曲线C1的方程.

(2)设P(x0,y0)(y0≠±3)为圆C2外一点,过点P作圆C2的2条切线,分别与曲线C1相交于点A,B和点C,D.证明:当点P在直线x=-4上运动时,点A,B,C,D的纵坐标之积为定值.

(2012年湖南省数学高考试题)

分析(1)曲线C1的方程为y2=20x.

(2)当点P在直线x=-4上运动时,点P的坐标为(-4,y0).又y0≠±3,则过点P且与圆C2相切的直线斜率k存在且不为0.由题意，每条切线都与抛物线C1：y2=20x有2个交点,则切线方程为

y-y0=k(x+4),

即

kx-y+y0+4k=0,

于是

整理得

(2)

设过P所作的2条切线PA,PC的斜率分别为k1,k2,则k1,k2是方程(2)的2个实根,故

设点A,B,C,D的纵坐标分别为y1,y2,y3,y4,则y1,y2是方程(4)的2个实根,所以

(6)

于是由式(3)～(6)得

因此，当点P在直线x=-4上运动时,点A,B,C,D的纵坐标之积为定值6 400.

评注本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第(1)小题用直接法或定义法求出曲线的方程;第(2)小题设出切线方程,把直线与曲线方程联立,由一元二次方程根与系数的关系得到点A,B,C,D纵坐标之积为定值,体现“设而不求”思想.

2.4 存在性问题

圆锥曲线中的存在性问题也很受高考命题教师的青睐.这类题的解题策略有2个：(1)先假设存在，然后建立等量关系,若能求出相应的量就存在，否则就不存在；(2)若能直接找到所求的量，则就能判断存在与否，进而解决问题.

(1)求曲线C的方程.

(2)动点Q(x0,y0)(-2

(2012年江西省数学高考试题)

分析(1)曲线C的方程:x2=4y.

解得点D,E的横坐标分别是

则

又因为

所以

对任意x0∈(-2,2),要使△QAB与△PDE的面积之比是常数,t只需满足

解得t=-1,此时△QAB与△PDE的面积之比为2.故存在t=-1,使△QAB与△PDE的面积之比是常数2.

评注本题以平面向量为载体,考查抛物线的方程、直线与抛物线的位置关系以及分类讨论的数学思想.

2.5 综合性问题

圆锥曲线中最值、范围、定值及存在性等综合性问题，它涉及到圆锥曲线的定义、几何性质、直线与圆锥曲线的位置关系，同时又与三角函数、函数、不等式、方程、平面向量等代数知识紧密联系.解这类问题时，需要有较强的代数运算能力和图形识别能力，能准确地进行数与形的语言转换和运算、推理转换，并在运算过程中注意思维的严密性.