整合切线定义 理解概念内涵——一堂有关切线概念的高三复习课

●

(余姚中学 浙江余姚 315400)

整合切线定义理解概念内涵
——一堂有关切线概念的高三复习课

●俞萍

(余姚中学 浙江余姚 315400)

1 背景介绍

前苏联教育家苏霍姆林斯基说过，学生通过自己的努力去理解的东西，才能成为自己的东西，才是他真正掌握的东西．孔子也说过:“不愤不启，不悱不发，举一隅不以三隅反，则不复也．”所谓“愤”，就是当学生心求通而未达的时候才去开导他；所谓“悱”，就是当学生口欲言而未能的时候才去启发他．这就是说，我们的教学应注重启发式教学，引而不发，让学生多思考，多实践．但是启发式教学也要考虑学生主体对知识的“饥渴”程度和学生对知识的掌握程度，在恰当的时机展开往往会事半功倍．

在高三的复习中，笔者感觉学生对切线的概念理解比较混乱，主要表现在以下3个方面：(1)学生最先接触的是初中圆的切线，几何直观性非常强．随着课程的进一步发展，他们又感受了圆锥曲线的切线，还没从这些复杂多变的切线中缓过神来，函数曲线的切线又再一次冲击头脑．在这个知识复杂多变、螺旋上升的过程中，学生的内心经历着强烈的认知冲突．(2)我们不少教师在上新课时往往轻概念教学，重解题训练，学生往往囫囵吞枣，不求甚解，如到底什么是切线？与曲线有且只有一个交点的直线是不是切线？切线是不是与曲线有且只有一个切点？(3)切线问题纷繁复杂，但我们的复习是章节性的，如果教师不引导的话，学生还是把圆锥曲线的切线和一般函数曲线的切线孤立地看待，不会主动建构切线概念，使之有机统一．这些现状给后续学习带来了较大的影响，同时学生对于理解整合切线概念的意愿也非常强烈．在这个背景下，笔者有意识地安排了一堂切线的复习课，展开启发式教学，尽可能地把切线问题包罗进来，主要以问题串的形式进行．

2 课堂实录

2.1 切线的表象，让我们感受直观

师：从初中开始我们就接触切线了，大家也感受着各种各样的切线，这堂课我们就围绕切线，展开深层次讨论，希望通过这堂课，大家对切线的认识更清晰．请大家在下面图1～图4中各画出一条切线．观察图形，对于切线你有何理解？

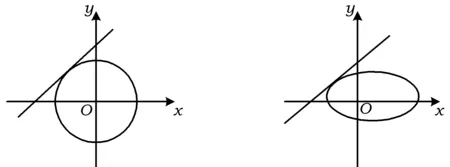
图1 图2

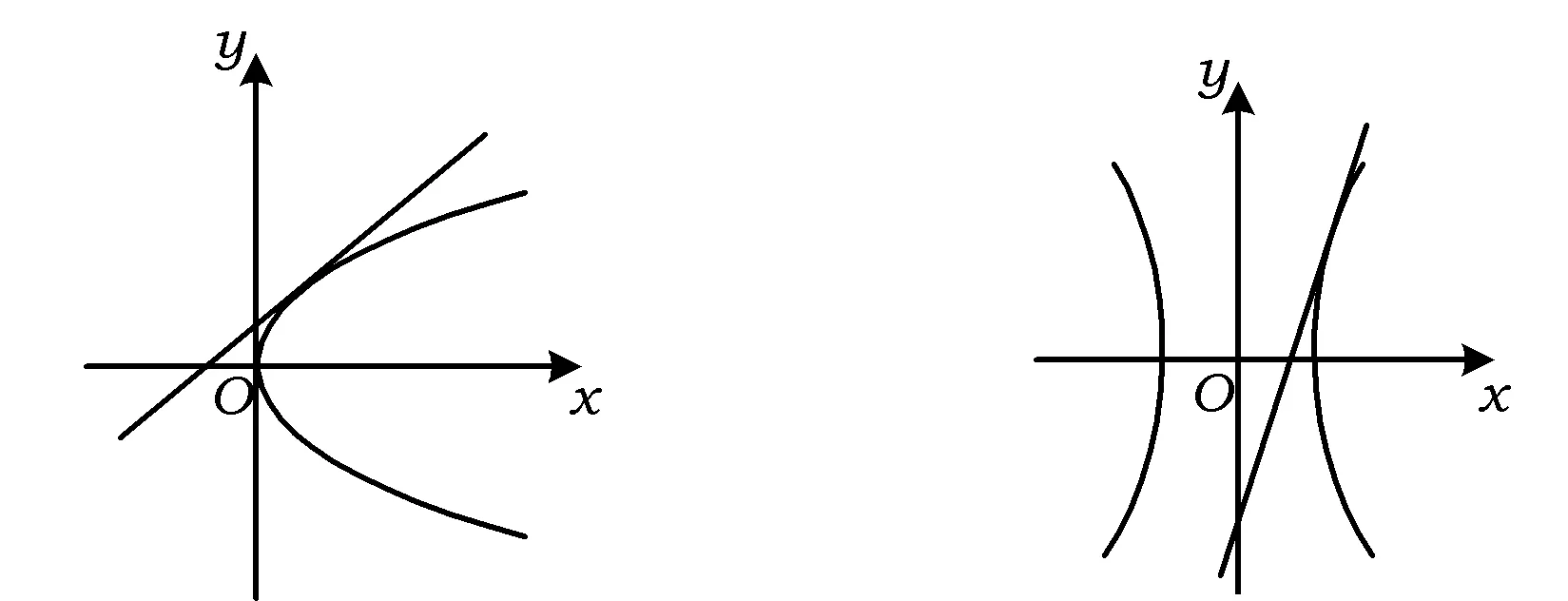
图3 图4

由于是复习课，学生非常快捷地画好了，笔者把一位学生的图用投影仪展示在黑板上．学生们讨论起来．

生1：圆和椭圆的切线非常直观；抛物线也还好，但是图形不封闭，给了我们一些遐想；双曲线的切线更复杂了．

生2：图1～图3中，过曲线内一点不能作曲线的切线，过曲线上一点能作曲线的一条切线，过曲线外一点能作2条切线．图4中的双曲线问题我说不准．

笔者点头微笑地看着学生，默不作声．

生3：图1～图3中的曲线都在切线的一侧，图4中的曲线在切线的2侧．

生4：图1～图4中的切线与曲线都有且只有一个交点．

生5马上反驳：在图4中，这条直线会不会与双曲线在右支相切的同时还与左支相交？

旁边也有几位学生齐声附和，教室里开始议论纷纷．

生6：不会与左支相交的．这条线比双曲线的渐近线要陡．

双曲线有左、右2支，又是不封闭曲线，因此它的切线相对复杂，从上面的回答中，笔者看到学生的问题也主要集中在双曲线上．由于目前课标对双曲线的教学要求不高，笔者不打算在课堂上耗费时间，因此对于生2关于双曲线的的说法笔者并没有展开讨论．但生5的问题非常实际，它也是一次巩固数形结合思想的好机会．笔者在肯定生6的同时，顺水推舟，引导他们往数的角度想．

师：形缺数时难入微．我们知道，从代数角度看，直线和双曲线方程联立，得到最多的是二次方程，最多2个实根．相切时二次方程Δ=0，已经有2个相等的实数根了，因此它不可能还与左支相交．

不少学生若有所思地点点头，对笔者的回答较为满意．

生7马上接了上来：哦！我懂了．那就是说，也不可能出现直线与双曲线左支和右支同时相切的情形了，对吗？

师(小结)：你说得太棒了！前面其他同学也都说得相当好，把切线的表象看得准确且到位．其中双曲线的问题要复杂很多，考虑到课标的要求，这里就不过多展开讨论，有兴趣的同学可以课后和我交流．这里的3类曲线：圆、椭圆和抛物线，它们的切线方程在前面的课中已经进行了深入研究．由最简单的圆x2+y2=r2引出了一条重要的直线x0x+y0y=r2，它的内涵十分丰富．当点P(x0,y0)在圆x2+y2=r2上时，方程x0x+y0y=r2表示的是在点P处圆的切线方程；当点P(x0,y0)在圆x2+y2=r2外时，方程x0x+y0y=r2表示的是过点P作圆的2条切线，切点弦所在的直线方程；甚至当点P(x0,y0)在圆x2+y2=r2内时，方程x0x+y0y=r2也有实际意义．我们把它推广到椭圆和抛物线，也有类似的结论，可见数学是多么和谐的统一！

学生纷纷点头赞同．

2.2 切线的内涵，让我们把握精髓

透过现象看本质，有了前面的铺垫，笔者又顺理成章地引出下面的问题．

师：前面我们感受了切线的表象，师生一起努力，肯定了生4的说法，上面4幅图中切线确实都与曲线有且只有一个交点．那么是不是所有的切线都与曲线有且只有一个交点呢？

生8不假思索地回答：是的吧．连最复杂的双曲线也符合．

师：真的吗？你的想法也不错，圆锥曲线确实符合，其他的呢？大家好好想想，不妨试着跳出圆锥曲线．

大多数学生沉默下来了，教室里十分安静，学生动笔在纸上画，在找反例．

过了一会儿，很多学生已经找到了．笔者又把一位学生的画投影在黑板上，如图5，函数的图像和它的一条切线，简单明了．

这里笔者真切地感受到：从上课开始师生一直在圆锥曲线的范围里研究，学生不自觉地把切线给孤立了起来，形成了思维定势，想当然地下结论．如果笔者放在一般函数曲线的情境中，这个问题对学生来说也不是很难．一旦跳出圆锥曲线，学生豁然开朗，是一次思想的飞跃．

师：看来切线不一定与曲线有且只有一个交点．那么反过来，是不是所有与曲线有且只有一个交点的直线都是它的切线呢？

学生们拿着现成的图1～图5做文章，迅速画出了图6～图8．笔者一边欣赏着学生的作图，一边故意试探着提问．

图5 图6

图7 图8

师：为什么图6～图8中这些直线不是切线？

生9：这类直线显然不是切线，是直线和曲线相交，但这是直观感觉，理由说不出来．

生10：切线是一条直线与曲线的2个交点无限接近以至重合形成的，这些图不符合．

……

师：在图8中，把直线往下平移成直线y=0，它和函数y=x3的图像是相交还是相切呢？

生11：应该也是相交．

生12：直线y=a(a≠0)是函数y=x3图像的切线肯定没错，但是直线y=0不好说，总感觉这条线和别的切线不一样．

生13：是的，这条曲线在原点2侧的凹凸性是不同的．

生14站了起来：是切线没错．我求了函数y=x3在x=0处的切线方程，正好是直线y=0．

教室里突然安静了下来，生14的回答影响力挺大的．有不少学生拿起笔，将信将疑地求了起来．

安静片刻之后，学生终于形成一致意见：这条直线确实是曲线的切线．

笔者由衷地佩服学生的智慧．但深层次里，学生对这条切线还是有些不认同的．著名数学家冯·诺依曼认为，数学兼有演绎科学和经验科学这2种特征，经验科学对学生更好地理解数学内涵大有裨益．而该函数涉及的凹凸性、拐点处的切线对学生来说是陌生的．

师：没错，直线y=0正是函数y=x3图像在(0,0)处的切线，它也是割线的极限位置，大家可以直观感受，以后大学里我们还要深入学习．

2.3 切线的外延，让我们深化认识

对切线有了深层次理解之后，笔者继续诱“敌”深入，把切线问题进行到底．

师：前面我们感受了与曲线有且只有一个交点的直线不一定是曲线的切线，切线也不一定与曲线有且只有一个交点，真是让人大开眼界．事实上，大家回忆一下，我们经常在做这类题：求在点P处的切线方程和过点P的切线方程．对过点P的切线我们要有清醒的认识，此时点P可以在曲线上，也可以在曲线外．当它在曲线上时，这个点可以不是切点，图5就是一个很好的例子．

笔者因势利导，又提出了新的挑战：请大家在我们学过的函数曲线中，再画画切线，看还有没有别的收获？

生15兴奋地站了起来：老师，看这幅图．

笔者把生15的图9展示了出来，函数y=sinx与y=1的图像．其实高中阶段涉及的函数类型并不多，这幅图的出现在意料之中，笔者故作惊喜状．

图9 图10

师：你有什么发现？

生15激动的心情溢于言表：这条切线与曲线有无数个切点了！

一下子，整个教室热闹了起来，学生们都很兴奋．

师：非常好！世界之大，无奇不有．小小的一条切线竟然与曲线有无数个切点．

生16：老师，那直线y=0是不是函数y=|x|图像的切线？见图10．

生17脱口而出：是的，它也是割线的极限位置呀．(停顿了一下)但是这条线好像又与前面的割线不太一样，在原点处它是尖尖的，也不敢肯定了．

如果学生不问这个问题，笔者是刻意回避的，毕竟不可导等概念都是大学里的内容，高中也不可越俎代庖．学生冷不丁地冒出了这个问题，于是笔者作了下面的回应．

师：大家的想法挺好的．这条线确实与前面的不一样，直线y=0其实并不是函数y=|x|图像的切线，这块内容我们在大学里将继续深入学习，以后大家就明白了．

2.4 切线的发展，让我们了解历史

通过上面由浅入深、由表及里的问题，学生们对切线有了一个较为系统的认识．临近下课时，笔者从切线的发展史角度，借助于幻灯片(一系列的数学家及他们的成就)，对这堂课进行了回顾和总结．

师：这堂课我们经历了伟人的思维历程，这也是很不平凡的切线发展历史．从数学家欧几里得到阿波罗尼斯，再到阿基米德，他们都从“公共点的个数”来看待圆锥曲线的切线．对圆锥曲线切线定义的局限性，大家都采取回避的态度，这个问题一直没有得到实质性进展．直到17世纪，数学家重新对曲线的切线问题进行了深入的研究．其中较有影响的是法国的费马和笛卡儿、德国的莱布尼茨和法国的洛比达，等等．他们跳出了从公共点个数、切线和曲线的位置关系等思维的束缚，从极限的思想指出了切线是割线的极限位置，是连接曲线上无限接近2点的直线，真正反映了切线的直观本质，体现了微积分中重要的思想——以直代曲．进入大学之后，还将深入学习．

最后，针对文科实验班学生的实际情况，笔者布置了一道作业探究题：通过课后讨论、查找资料等方式，围绕我们做过的习题，对抛物线的一般切线问题做深入的探究．

下课铃响了，学生们意犹未尽．笔者知道，这节课的收获是不小的．

3 几点思考

《数学课程标准》指出：“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上．教师应激发学生的学习积极性，向学生提供充分经历数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验．学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者．”本课例正是朝着这个方向努力的．

3.1 概念是数学解题的前提

高三的复习课很多，很多教师感慨复习课上什么内容好．一轮复习结束了，二轮复习又接着“炒冷饭”，中心就是围绕“解题”，学生累，教师也累．在这个过程中，我们往往忽视了数学概念对解题的作用．其实，解题教学与概念教学是相辅相成、互为补充的．如果在复习阶段，学生对于切线内涵还是处在懵懂状态，这对他们的学习是十分不利的．学生在理解概念的同时，也在理解数学，因此对于概念性的复习课，教师要舍得给时间．

3.2 认知是知识重组的保证

本堂课的时间跨度相当大，涉及了整块切线内容的复习．而对于切线的学习，经历了初中圆的切线，过渡到圆锥曲线的切线，再延伸到一般曲线的切线．随着知识的螺旋上升，学生对切线由感性认识上升为理性分析．但是，高中的切线复杂多变，和学生头脑中根深蒂固的圆的切线大相径庭，知识点上也各自为政、杂乱无章，这时，知识的重现、重组十分有必要，复习课正是给我们提供了这样一个整合各知识模块的平台．

3.3 问题是主动探究的动力

思维从问题开始，好的问题能使思维得到真正的提高．本节课“以问题为中心”来组织教学过程的各个环节，把问题贯穿于教学过程的始终．笔者认为教师最主要的是完成知识点的牵线搭桥，最关键的是通过有效设问激发学生的思维深度.通过问题探究，变“被动接受”为“主动探究”，培养学生的探究能力；变“教师讲解”为“学生主讲”，发挥学生的主体作用；变“划定框架”为“自由思考”，培养学生的发散思维．对于每一个问题，努力让学生独立思考或通过学生合作交流来获得结果．实践证明，通过这堂课，学生对切线的认识更多了，对切线内容的学习更有信心了．

3.4 兴趣是学生成功的源泉

兴趣是最好的老师．只要把学生学习数学的兴趣充分调动起来，一定能学好数学．如何培养学生的兴趣，是永恒的话题．维果茨基认为教师在教学设计时，应分析并估计学生的最近发展区，让学生努力经历“跳一跳，够得着”的思维历程，品味成功的喜悦．当学生得到一个小小进步的时候，我们要给予积极的正面评价．本堂课中，问题设置由浅入深，善于从学生的问题中发现问题，敢于放手让学生思考，鼓励学生自己发现问题、解决问题，在一次又一次的思维碰撞中让学生不断地否定自我又完善自我，品尝成功的喜悦．师生双向互动交流，在提升学生能力的同时，也真正实现“教学相长”．

[1] 殷克明．高中生对切线的理解——历史相似性研究[D]．上海：华东师范大学硕士学位论文，2011．