从一道高考题谈平面向量与复数的关系
2013-10-26
●
(兰溪市教研室 浙江兰溪 321102)
从一道高考题谈平面向量与复数的关系
●沈联晖
(兰溪市教研室 浙江兰溪 321102)
在高中数学中,“平面向量”和“复数”是看似无关的2块知识,前者出现在必修4,后者在选修2-2中.在平时教学中,教师一般不会将“平面向量”作为“复数”的先行组织者组织教学,更不会在学习平面向量时想到为以后学习复数埋下伏笔,在高三复习时也很少将2块内容放在一起进行比较.但2010年浙江省数学高考理科卷的第5题给我们一线教师上了很好的一课,原题如下:
试题对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是
( )

(2010年浙江省数学高考理科试题)
当年这道题错误率甚高,主要表现在:有些学生不会对不等式知识进行迁移和应用,看不懂|z|≤|x|+|y|;有些学生将复数运算和向量运算混淆,类比|a|2=a2=x2+y2,误认为z2=x2+y2正确;并且很多学生由于解决该题受阻而影响了考试情绪,使后面的解题方寸大乱,堪称“最险恶的容易题”.这暴露出平时教学和复习的缺失,学生没有深刻理解向量和复数的意义、计算法则,也没有将这2块知识点的共性和各自的特性梳理清晰.为此,笔者将自己在教学实践中总结出的2块知识之间的关系以及学生易混淆的知识点呈现如下,以飨读者.
1 向量与复数的区别、联系

向量有“形”的功能还表现在具有平面内2条直线的位置关系,常用的结论是:2个非零向量a与b垂直的充要条件是:a·b=0;2个非零向量a与b平行(共线)的充要条件是:b=λa,λ∈R(写成坐标形式为:设a=(x1,y1),b=(x2,y2),若a⊥b,则x1x2+y1y2=0;若a∥b,则x1y2-x2y1=0).这是复数所没有的.
形如a+bi(a,b∈R)的数叫复数,a为实部,b为虚部,i为虚数单位,常记作复数z=a+bi.有些学生常将复数误写成z=(a,b),教师要时常提醒学生注意:一般2个复数只能说相等或不相等,而不能比较大小,具体可参考文献[1];2个复数相等充要条件为:a+bi=c+di⟺a=c,b=d(a,b,c,d∈R).利用复数相等的充要条件,可以得到关于实数的方程(组),通过解方程(组),求出待定系数的值.
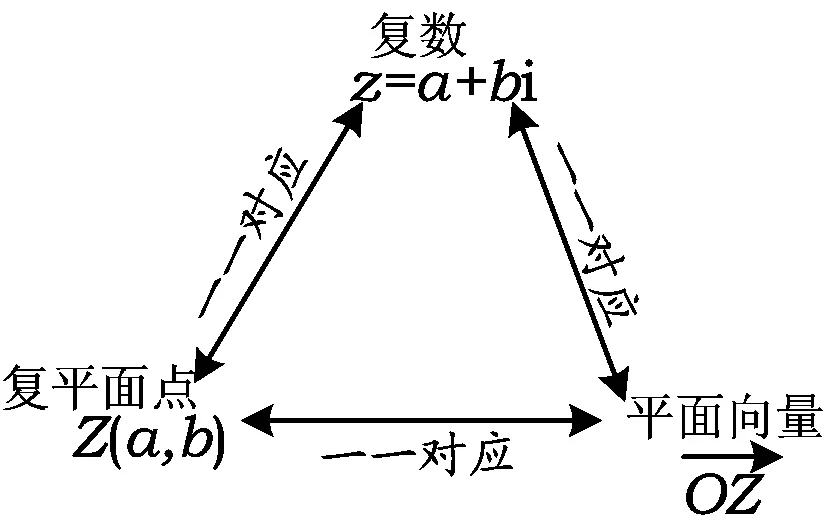
图1
向量是近代数学中重要和基本的数学概念之一,有深刻的几何背景,是解决几何问题的有力工具,运用向量方法可将几何性质的研究转化为向量的运算,使几何问题通过向量运算得到解决[2].人教A版《数学(必修4)》“2.5.1平面几何中的向量方法”一节中的2个例题让我们领略到用向量法证明几何题的风采.复数的引入是解决实际需求和数学内部的矛盾在数系扩充中产生的.复数尽管是数,它可以用复平面上的点表示(类比实数可用数轴上的点表示),也就是复数z=a+bi(a,b∈R)可以用坐标平面上的点Z(a,b)表示,它实际上是一有序实数对.在i和j是单位正交基底的前提下,向量ai+bj可用平面直角坐标系中的点(a,b)表示,因此复数z也可用向量表示,只要以a+bi对应的点Z(a,b)为终点,以原点O为起点画向量即可,于是有如图1所示的关系[3].

因此讨论复数的运算、性质和应用时,就可以在复平面内用向量的方法进行.如:
复数z1=3+i,z2=2+i,m是实数,则|mz1-z2|的最小值为______[4].
此题固然可用以下方法来解:

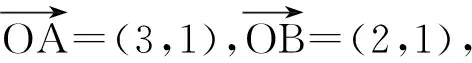

图2
又如2010年浙江省理科第5小题选项D:


2 相反向量与共轭复数
长度相等且方向相反的向量叫相反向量.如向量a的相反向量为-a,几何意义是表示2个向量的有向线段长度相等,方向相反.有了相反向量,便可以通过向量加法定义向量减法,如a-b=a+(-b).长度为0的向量叫零向量,记作0(很多学生易错写成0,或者不分场合乱用0和0),有a+(-a)=a-a=0(特别注意:0·a=0,但0·a=0).长度等于1个单位的向量叫做单位向量.长度相等且方向相同的向量叫做相等向量,记作a=b.
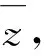
3 运算法则和运算律的比较
考虑到向量的坐标形式和复数有相似之处,在此仅研究向量的坐标运算与复数运算的比较(其中表1是运算法则的比较,表2是运算律的比较):

表1 运算法则

表2 运算律
4 容易混淆的运算比较

(2)|a+b|2=(a+b)2=a2+2a·b+b2(在空间向量中解决立体几何题有广泛的应用),而|z+1|2≠z2+2z+1.一般设z=a+bi,a,b∈R,则|z+1|2|=|a+1+bi|2=(a+1)2+b2,或从几何意义看,表示复数z的点Z到-1的距离的平方.
[1] 胡典顺.为什么复数不能比较大小[J].数学通讯,2012(1):23-24.
[2] 刘绍学.数学4教师教学用书[M].北京:人民教育出版社,2007:67.
[3] 刘绍学.数学选修2-2教师教学用书[M].北京:人民教育出版社,2007:93.
[4] 杨苍洲.善用习题变式教学,促进学生认知发展[J].数学通讯:下半月,2012(11):10.
[5] 黄小红.“复数的几何意义”的教学实践与思考[J].中国数学教育,2010(1/2):52-53.
[6] 范素杰,郜舒竹.向量为什么不存在除法[J].中小学数学,2012(4):11-13.
