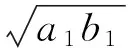剖析代数式结构 多视角妙解高考题
2013-10-26
●
(昌硕高级中学 浙江安吉 313300)
剖析代数式结构多视角妙解高考题
●吴忠
(昌硕高级中学 浙江安吉 313300)
数学中有一种美,即结构对称美,很多代数结论具有这样的对称美,解决代数问题总会遇到代数式结构的变形和转化,然而代数式的结构变化不可能唯一,总会有很多不同的变形方向,不适当的变形会让解决问题的思路受到阻碍,适当的代数变形总能给人以灵感与思维的火花,从而胜利到达成功的彼岸.代数式的转化方向总是与现有知识基础联系在一起,总会在所学知识的附近搜索类似结构的定理、定义、性质及规律等,因此在课堂上帮助学生分析某些数学结论的代数结构特征、类型显得非常重要,应该让学生从结构变形中去体会数学思想方法,从而培养学生良好的思维习惯和较强的思辨能力.本文试图从一道题的代数结构不同角度的分析找到解决某些代数问题的基本途径.
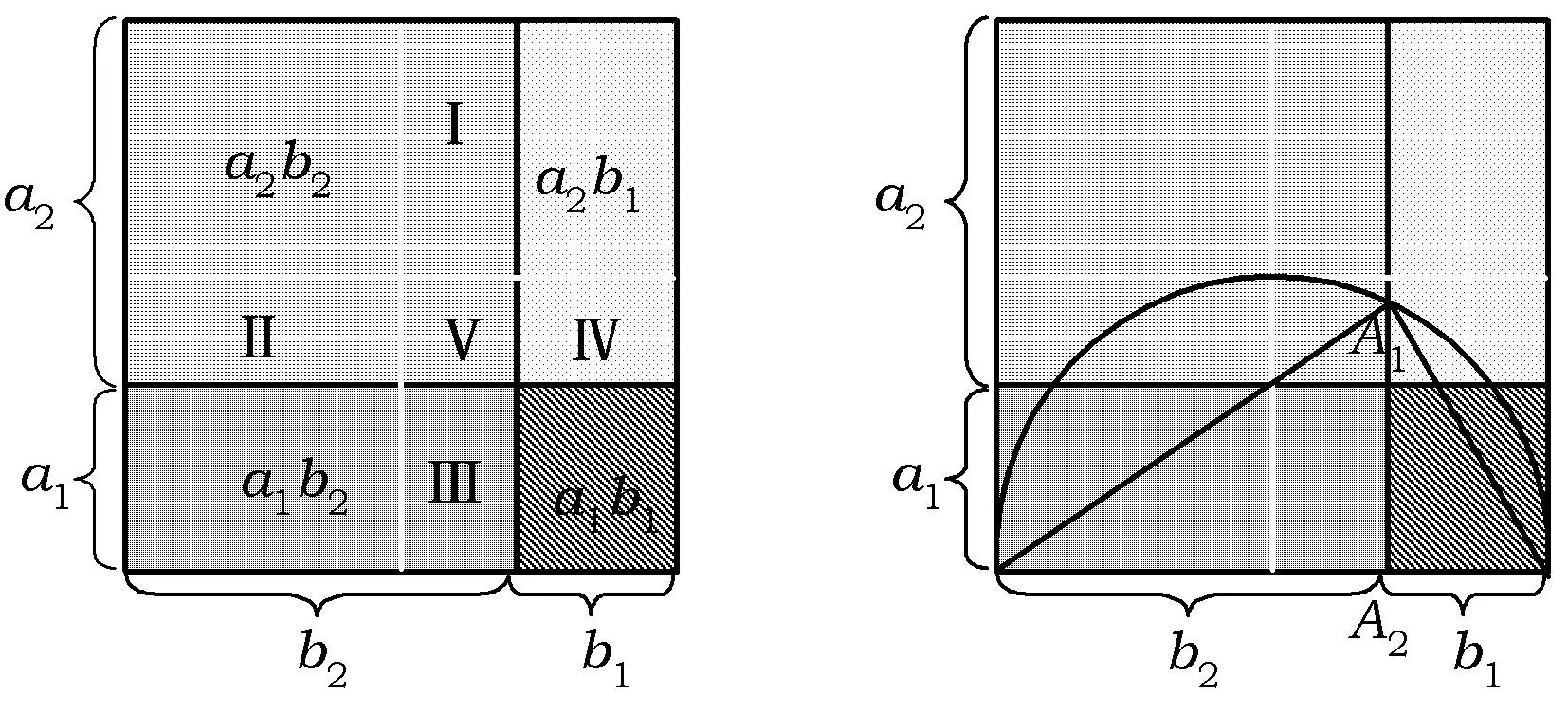
题目若0 ( ) A.a1b1+a2b2B.a1a2+b1b2 本题选自2008年江西省数学高考理科试题第9题,主要考查的知识点为不等式的性质,包括比较不等式的大小及不等式结构的认识与理解.本题解法比较开放,思路较宽,但学生不容易切入,看似能解决,但真正要比较出4个代数式值的大小却比较难.本题除了考查学生对不等式基础知识、基本技能的掌握程度外,还考查学生在代数式的变形、运算等方面的能力,考查学生对数学问题的观察、分析及思辨能力. 1.1 分析问题的已知条件 本题已知2组数各自的大小关系及2组数的和为定值1,解决的问题是比较2组数不同对应积之和的大小关系,问题反映出代数式和积之间的关系、不等与相等之间的关系、相似代数式结构之间的关系. 1.2 分析问题的隐含条件 本题对于基础一般的学生来说,最直接有效的办法是特殊值法,但如果作为教学例题,要排除4个代数式值的大小关系必须分析原因,难点在于如何构造出不同对应积的和式及对这些代数式的变形.本题隐含条件和潜在信息为2个正数和为定值且这2个数有大小关系,就可以比较出2个数与定值之间的大小关系.2组数之间即有着相对的独立关系,又可以相互联系在一起. 1.3 分析解决问题的关键 本题的主要方法是能运用综合法及分析法来解决问题,能从选项中观察到代数式结构之间的关系,从而找到问题的突破口.能用通性通法(作差、作和法)及代数式常见变形与构造为切入口,不断寻找到条件与结论的关系,达到融会贯通的目的. 2.1 特殊值法 本题从条件来看a1,a2,b1,b2均为不定值,且a1+a2=b1+b2=1,本题题型又为选择题,据上分析可以选择特殊值法得出答案. 解法1令a1=0.2,则a2=0.8,再令b1=0.4,则b2=0.6,通过计算可知选项A的值为0.56,选项B的值为0.4,选项C的值为0.44,而选项D的值为0.5,故选A. 2.2 作差(和)法 从选项中可以看出,选项A,B,C的结构相似,联想运用比较大小的常用方法——作差法,作差后可以分解因式,通过因式正负性的判断可确定A,B,C的大小关系. 解法2因为 A-C= (a1b1+a2b2)-(a1b2+a2b1)= (a1-a2)(b1-b2)>0, 所以 A>C. 又因为 A+C= (a1b1+a2b2)+(a1b2+a2b1)= (a1+a2)(b1+b2)=1, 所以 又 B-C= (a1a2+b1b2)-(a1b2-a2b1)= (a1-b1)(a2-b2), 因为 a1+a2=b1+b2=1, 所以若a1≥b1,则a2≤b2;若a1 B≤C, 因此 故选A. 2.3 排序不等式法 注意到选项代数式的结构,有2组数并且2组数有一定的大小关系,结论又是2组数的积之和的大小关系,故可以联想运用排序不等式来解决问题,只要能找到2组大小顺序排定的数组即可用排序不等式构造结论所需要的代数式. 解法3因为0 a1b1+a2b2>a1b2+a2b1, 所以 A>C. 又因为 a1+a2=b1+b2=1, 所以 从而 由排序不等式得 a2b1+a1b2≥a1a2+b1b2, 而 于是 故选A. 2.4 直接代入消元法 本题4个数之间既有相等关系,又有不等关系,条件与结论都涉及到4个字母参数,因此想到应用代入消元法,通过代入运算后再进行比较,可以让代数式所涉及的字母减少,有利于对代数式值的大小进行判别.在代数式变形过程中通过换元、消元、变元等方法减少字母参数也是解决数学问题的常用方法. 解法4令a1=1-a2,b1=1-b2,则 A-B= (1-a2)(1-b2)+a2b2-(1-a2)a2- (1-b2)b2= (a2+b2)2+1>0, 从而 A>B. 又A-C= (1-a2)(1-b2)+a2b2-(1-a2)b2- (1-b2)a2= 1-a2-b2+a2b2+a2b2-a2+a2b2-b2+a2b2= 1-2(a2+b2)+4a2b2=(1-2a2)(1-2b2), 因为 0 且 a1+a2=b1+b2=1, 所以 从而 (1-2a2)(1-2b2)>0, 故 A>C. 又B-C= (a1a2+b1b2)-(a1b2-a2b1)= (a1-b1)(a2-b2)=-(a2-b2)2≤0, 从而 B≤C, 即A>C≥B.故选A. 2.5 中值换元法 消元的方法除直接代入消元法、作差消元法外,还可以采用换元消元法,即通过计算比较2个代数式的大小.注意到已知条件中2个数和为定值1,故可以采用中值换元来达到减元、计算、比较的目的. 又s2+t2≥2st,显然代数式中的最大值为A. 2.6 构图法 注意到选项结论中代数式结构是正数积之和,因此联想到初中教材中平方和公式的面积证法,构造适当的图形,运用面积来解决问题. 图1 解法6如图1构造边长为1的正方形,可知 因为 a2>a1>0,b2>b1>0, 所以 SⅠ>SⅢ,SⅡ>SⅣ, 即 通过画以正方形边为直径的半圆可知 同理 故 故代数式中的最大值为A. 2.7 向量法 通过观察可以发现,选项所给结论的结构特征正是向量内积的坐标形式,因此可以通过建立适当的直角坐标系,通过设定符合条件的向量坐标来构造结论所需的结构形式,运用向量内积的性质解决问题. 图2 解法7如图2建立直角坐标系,在线段PM上取2个点并设A(a1,a2),B(b1,b2),由图可知点A,B关于OP对称的点坐标为A′(a2,a1),B′(b2,b1),则 点B在点A的上方时也成立,因此 a1b1+a2b2>a1b2+a2b1. 从而 故这4个代数式中A的值最大. 以上方法抓住了问题条件及结论中代数式的结构特征而采取相应的解题策略.本题虽然可以用特值法寻找问题的答案,但在教学过程中需要教师对其进行有理有据的分析,对本题的剖析应定位于对式的结构分析,从而联想正确的解题方法.选项中的代数式无论是通过代数构造还是几何构造,其灵感都来源于原有较扎实的基础知识和对于代数式结构特征的联想. 3.1 变结论 变式1若0 ( ) 分析对选项的结论平方后可以转化成与原题相仿的题,代数式中值最大为A. 3.2 变条件 ( ) A.a1b1+a2b2B.a1a2+b1b2 分析可以利用上述的向量法,构造单位圆,在直线y=x上方部分取任意2个点A(a1,a2),B(b1,b2),可知点A,B的坐标满足条件,将选项结论转化为向量式的运算,可比较出大小,最大值为A. 3.3 变维度 变式3若0 ( ) A.a1b1c1+a2b2c2B.a1b2c1+a2b1c2 分析可以利用排序不等式解决问题,代数式中值最大值为A. 3.4 变特殊为一般 关于变式还可以从其他角度进行变化,在此不一一阐述. 本题从拟题的角度来看,可以从2个层面来揣测出题者的意图:一方面如果学生认为比较难,便可以运用特殊值法来猜想答案,虽然没有百分之百的正确率,但也可以看出学生是否具有观察、猜想、应变的能力;另一方面如果学生想百分之百解决此题,那必需要有较扎实的不等式的基础知识、较熟练的运算技巧、较强的思维能力和较深的数学思想为支撑,这也是高考考查的重点.本题既可以用通性通法(作差法、代入消元法),也可以用特性特技法(中值换元法、排序不等式、向量法、构图法)等,因此入口比较宽,但都不是一步能到达预期目标.本题的关键点是能挖掘出题目中隐含的信息,切入点是观察代数式相似结构之间的关系,在已学相应知识的最近区联想类似解决问题的方法,从代数结构上突破难点.本题的变式主要对选项的代数结构做了变形,意在通过训练达到熟练剖析代数结构类型的目的,包括对式的构造和转化. 总之,在数学教学的过程中,不能盲目地追求数量不顾质量,采用题海战术,而应该去教会学生思考,培养学生善于思考.通过对代数式结构的分析,联系已学过的知识,从不同的视角入手解决问题,更能让学生的思维迁移、发散、开拓和活跃,提高学生思维的敏捷性和灵活性,从而提高分析与解答数学题的能力.通过变式训练,既能促使学生沟通知识点间的联系,又能培养学生的思维能力,从中学到转化与化归、数形结合、函数与方程等基本的数学思想.同时学生可以通过对比、小结,得出自己的体会,充分发掘自身的潜能,从而提高学生的解题能力. [1] 李歆.2008年江西高考数学第9题的规律探究[J].数学通讯,2009(Z1):封三.
1 对问题条件与结论的分析
2 对问题条件与结论的代数结构分析





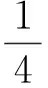


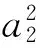

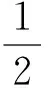



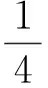
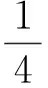



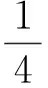



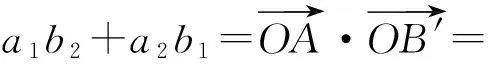




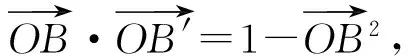




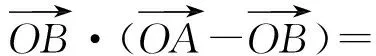

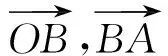

3 问题的变式