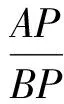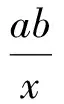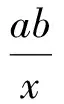妙建模型求最值
2013-10-26
●
(绍兴县实验中学 浙江绍兴 312030)
妙建模型求最值
●占新华毛幼娥
(绍兴县实验中学 浙江绍兴 312030)
几何最值问题近几年广泛出现在各地中考与竞赛试卷中.此类问题往往以平面图形或直角坐标系为载体,且形式多样,具有较强的综合性,对考生的能力要求较高.此类问题常具有很强的探索性,需要运用动态思维、数形结合、特殊与一般相结合、逻辑推理与合情想象相结合等思想方法解决,需要我们善于引导学生挖掘问题的本质,从中归纳出思想、方法.
本文试图从“妙建数学模型”入手,挖掘教学资源、注重多题一解,在培养学生知识迁移能力方面作一些尝试与探索.
1 妙用几何不等式模型
1.1 和最小模型
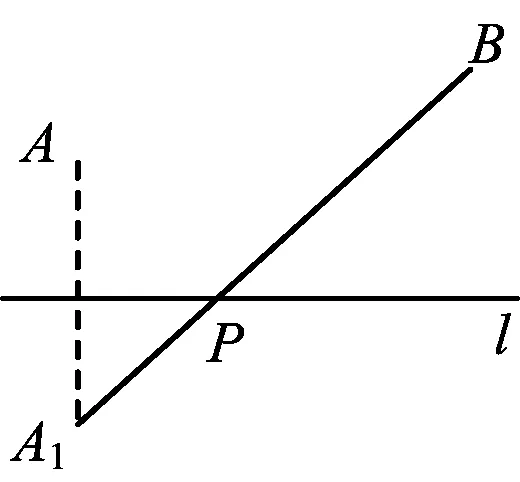
图1
“和最小模型”的一般表述是:如图1,已知A,B是直线l同侧的2个点,试在l上找一点P,使得线段PA与PB之和最短.
这里要注意:(1)A,B是已知直线l同侧的2个定点,P是l上的动点;(2)求的是当线段PA,PB的总长度最小时,点P在l上的位置.只有(1),(2)全符合时,才能使用“和最小模型”.
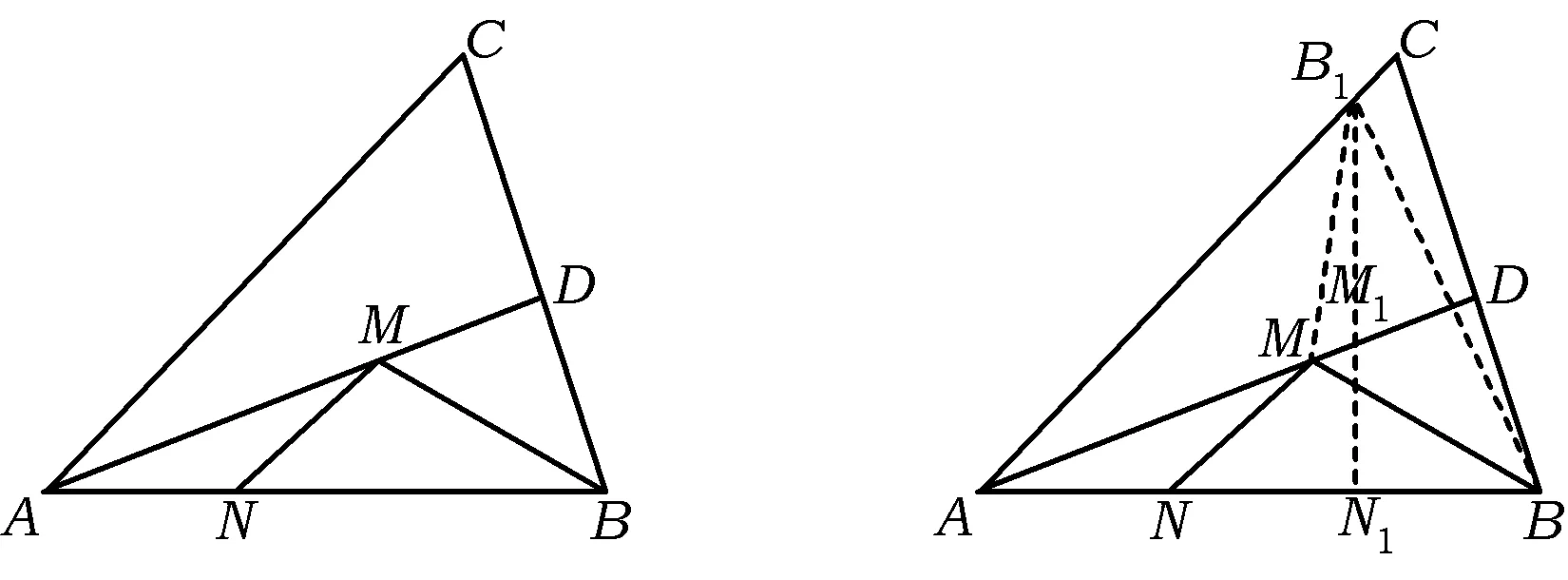
图2 图3
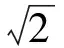
(2011年全国初中数学联赛武汉市选拔赛试题)
分析由于点M,N均在某个范围内连续变化,故应整体考虑,注意到平分关系,可以考虑轴对称变换,化“折”为“直”,利用最小值模型求解.
解如图3,因为AD平分∠BAC,可以作点B关于AD的对称点B1,联结B1M,再作B1N1⊥AB,垂足为点N1,交AD于点M1,则
BM+MN=B1M+MN≥B1N1,
当点M,N分别处于点M1,N1位置时,BM+MN=B1N1取到最小值.因为
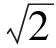
所以B1N1=4,即BM+MN的最小值为4.
例2河岸l同侧的2个居民小区A,B到河岸的距离分别为am,bm(即图4中所示AA′=am,BB′=bm),A′B′=cm.现欲在河岸边建一个长度为sm的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.
(1)在图4中画出绿化带的位置,并写出画图过程;
(2)求AC+BD的最小值.
(第21届江苏省初中数学竞赛试题)

图4 图5
分析同样是求2条线段和的最小值问题,不同之处在于2条线段AC和BD没有公共端点.注意到所给的绿化带CD的长是一个定值,若将线段AC(或BD)沿与直线l平行的方向平移与CD等长的距离,就可以使它们的一端重合,将问题转化成有公共端点的直线同侧2条线段和的最小值问题,从而使问题得到解决.
解(1)如图5,作线段AP∥直线l,使AP=s,且点P在点A的右侧,取点P关于直线l的对称点P1,联结BP1交直线l于点D,在直线l上点D的左侧截取DC=s,则CD即为所求绿化带的位置.
(2)由对称性得P1D=PD,又PD=AC,于是P1D=AC,若绿化带建于直线l上任一位置C1D1,则
AC1+BD1=PD1+BD1=P1D1+BD1≥BP1,
且当点D1在线段BP1与直线l的交点时等号成立,从而
AC+BD=P1D+BD=P1B=
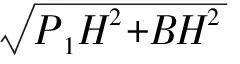
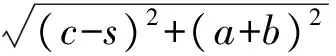
例3如图6,在边长为1的正方形ABCD中,点M,N,Q,P分别在边AB,BC,CD,DA上.如果AM=BM,DP=3AP,求MN+NQ+QP的最小值.
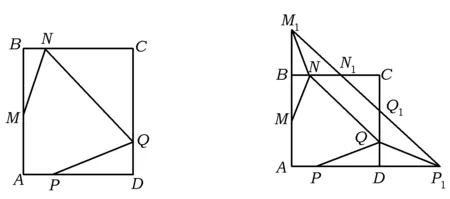
图6 图7
分析尽管本题变成了3条线段和的最值问题,但实质还是通过轴对称求最小值.
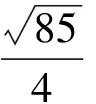
小结通过上面的例子可以看出,在求线段和的最小值时,往往运用“对称”或“平移”等方法,起到“化折为直”的作用,运用“两点之间线段最短”或“垂线段最短”等几何原理,巧用“和最小模型”以不变应万变,最终形成解决问题的基本策略.
1.2 差最大模型
“差最大模型”和“和最小模型”类似,下面举例说明.
例4如图8,已知点A(1,3),B(5,-2),试在x轴上找一点P,使|AP-BP|最大,求满足条件的点P的坐标.

图8 图9
分析点A,B在x轴的2侧,线段AP,PB的长度随点P在x轴上位置的改变而改变,在x轴上找不到特殊的位置使得|AP-BP|最大,于是考虑作点B关于x轴的对称点B1,使点A,B1在x轴的同侧,显然
|AP-BP|=|AP-B1P|.
当点A,B1,P构成三角形时,
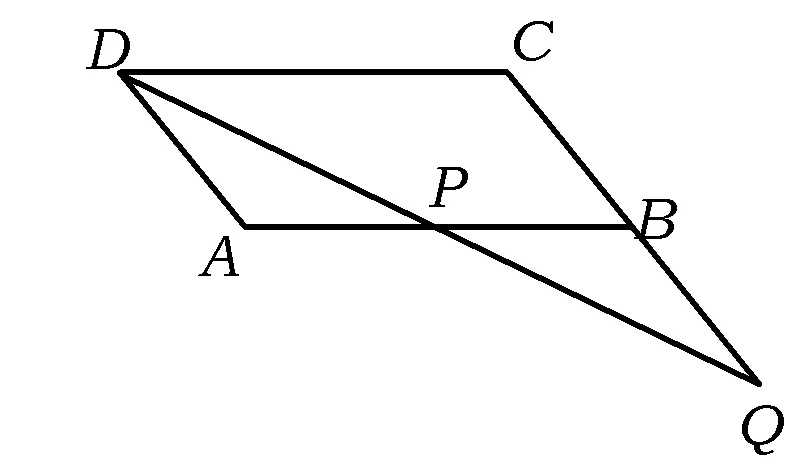
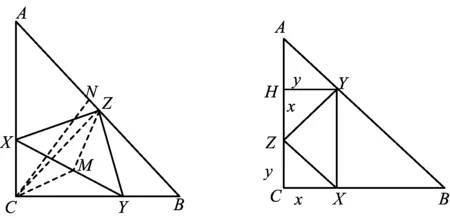
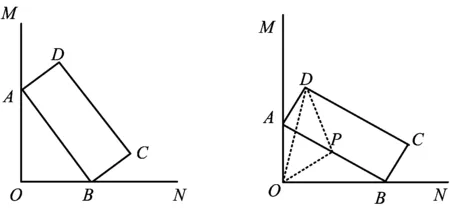
|AP-BP|=|AP-B1P| 当点P在直线AB1与x轴的交点处P1时(特殊位置), |AP-B1P|=AB1, 除了点P1外,另外在x轴上的任意一点都与点A,B1构成三角形.因此当点P在点P1的位置时,|AP-BP|最大. 解如图9,作点B关于x轴的对称点B1,则B1(5,2),可求得直线的解析式为 令y=0,得x=13,故点P(13,0). 图10 图11 例5如图10,∠MON=90°,矩形ABCD的顶点A,B分别在边OM,ON上,当点B在边ON上运动时,点A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1.在运动过程中,点D到点O的最大距离为 ( ) 分析如图11,取AB的中点P,联结PD,PO,在运动过程中,线段PD,PO的长度保持不变,联结DO.不难发现,当点D,O,P构成三角形时,DO 解取AB的中点P,联结PD,PO,则 通过上面的例子我们可以看到,在求“和的最小值”和“差的最大值”时,往往借助某个三角形模型,利用“三角形2边之和大于第3边”或“三角形2边之差小于第3边”得以解决. 由于几何最值都是在动点背景下产生的,当运用几何方法较难解决问题时,可以设某条变化的线段长为自变量,结合图形特点,构造函数或方程求最值. 2.1 基本不等式 可以利用如下基本不等式来求最值: 图12 例6如图12,已知平行四边形ABCD,AB=a,BC=b(a>b),P为AB边上的一动点,直线DP交CB的延长线于点Q,求AP+BQ的最小值. 解设AP=x,由△APD∽△BPQ,得 即 从而 又因为 2.2 构造一元二次方程 可以构造一元二次方程,利用一元二次方程必定有解的代数模型求最值. 例7已知△XYZ是直角边长为1的等腰直角三角形(∠Z=90°),它的3个顶点分别在等腰Rt△ABC(∠C=90°)的3条边上,求△ABC直角边长的最大可能值. 分析顶点Z在斜边上或直角边CA(或CB)上.当顶点Z在斜边AB上时,取XY的中点,通过几何不等关系求出直角边的最大值;当顶点Z在(AC或CB)上时,设CX=x,CZ=y,建立x,y的关系式,运用代数的方法求直角边的最大值. 解(1)如图13,顶点Z在斜边AB上,取XY的中点M,联结CM,ZM,CZ,并作边AB上的高CN,则 图13 图14 (2)如图14,顶点Z在直角边CA(或CB)上,由对称性,不妨设点Z在CA上,设CX=x,CZ=y,并过点Y作YH⊥CA于点H,易证△ZYH≌△XZC,得 HZ=CX=x,HY=CZ=y. 又△AHY为等腰直角三角形,则AH=y,设AC=b,则2y+x=b,即x=b-2y,在Rt△CXZ中, y2+(b-2y)2=12, 即 5y2-4by+b2-1=0. 因为y为实数,则 Δ=16b2-20(b2-1)=20-4b2≥0, 所以 适当选取变量,建立几何元素间的函数、方程、不等式等关系,再运用相应的代数知识求解,也是求几何最值问题的一种常用的方法.
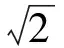

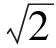
2 妙用代数不等式求最值