复射影空间中具有常平均曲率的全实子流形

刘 敏

（安徽师范大学 数学计算机科学学院，安徽 芜湖241000）

0 引 言

设CPn＋p是具有Fubini－Study度量的复n＋p维复射影空间，全纯截面曲率为常数4.设J为CPn＋p的复结构，Mn为CPn＋p的实n维子流形.如果Mn上每点切空间被J变换到自身，则称Mn是CPn＋p的全纯子流形.反之，若Mn上每点的切空间被J变换到该点法空间，则称Mn为CPn＋p的全实子流形.

关于CPn中的全实子流形研究目前已有许多结果［1－3］.沈一兵［4－5］讨论了CPn＋p中全实极小子流形，得到了关于数量曲率、Ricci曲率和截面曲率的Pinching定理：

定理1 设Mn是CPn＋p中紧致全实极小子流形，若

则M全测地.

定理2 设Mn是CPn＋p中紧致全实极小子流形，若Q＞n－2，n≥4，则M全测地.

定理3 设Mn是CPn＋p中紧致全实极小子流形，若

则M全测地.其中：S是M 的第二基本形式模长平方；K，Q分别是M 的截面曲率和Ricci曲率下确界.

本文将上述结果推广到具有常平均曲率的全实子流形，得到如下结果：

注1 当H＝0时，定理4即为定理1.

定理5 设Mn是CPn＋p中的n维具有常平均曲率的紧致全实伪脐子流形，若Mn的Ricci曲率的下确界Q＞n－1＋（n－1）H2，n≥4，则Mn全测地.

关于第二基本形式模长平方S，有：

定理6 设Mn是CPn＋p中的n维具有常平均曲率的紧致全实伪脐子流形，则

定理7 设Mn是CPn＋p中的n维紧致全实伪脐子流形，且Mn的平均曲率为常数，则Mn具有平行平均曲率向量.

1 预备知识

设Mn是CPn＋p中实n维全实子流形，J为CPn＋p的复结构.在CPn＋p上选取局部规范正交标架场：

使得限制于Mn，｛e1，…，en｝与Mn相切，约定各类指标的取值范围为：

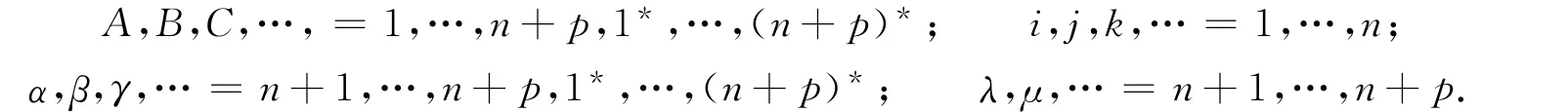
用｛ωA｝表示｛eA｝的对偶标架场，则CPn＋p的结构方程为

其中：

这里（JAB）为线性变换J关于｛eA｝的变换矩阵，即

其中In＋p为n＋p阶单位矩阵.

将上述形式限制在M上，则有：

其中Rijkl和Rαβij分别是Mn的Riemann曲率张量场和法曲率张量场关于｛eA｝的分量.进一步，Mn的平均曲率向量场ξ、平均曲率H与第二基本形式模长平方S及数量曲率ρ可表示为

引理1［6］设A1，A2，…，Am是m 个n阶对称矩阵（m≥2），则

引理2［7］设Mn是CPn＋p中的n维全实子流形，用TMn和T⊥Mn分别表示Mn的切丛和法丛，V＝J（TMn），V⊥表示V在T⊥Mn中的正交补丛，即T⊥Mn＝V⊕V⊥，ξ是Mn的一个平行脐性法向量场，则ξ必位于V⊥中，即ξ∈C∞（V⊥）.

2 定理的证明

由引理2选取en＋1与平均曲率向量ξ平行，结合Mn是伪脐，则

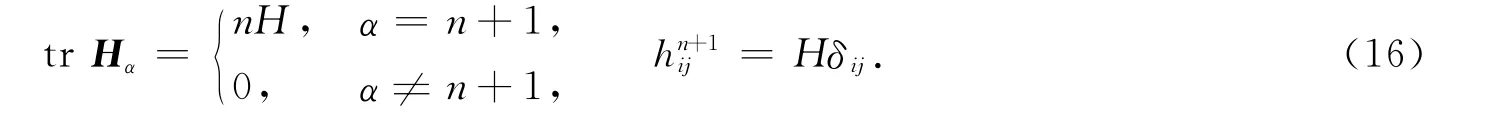
由式（4），（9），（11），（16）得

由式（17），（18），对任意实数a，有

引理3 设Mn是CPn＋p中的n维紧致全实子流形，其平均曲率H为常数，则

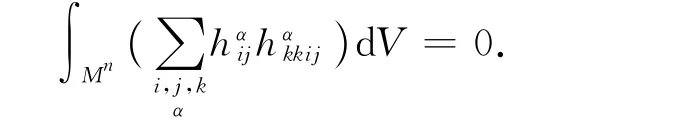
证明：由

2.1 定理4的证明

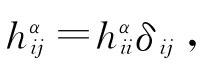
不等式（20）两边与标架选取无关，故关于α求和可得

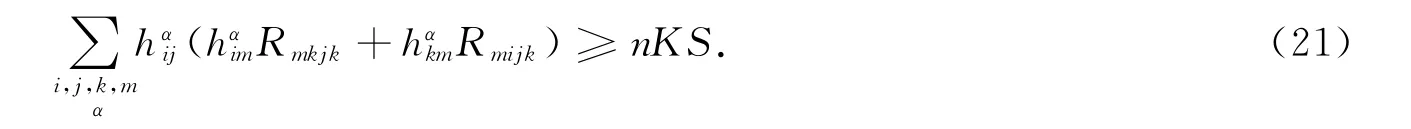
此外，由文献［9］，有

由式（19），（21）～（23）得

由式（25）可见，当

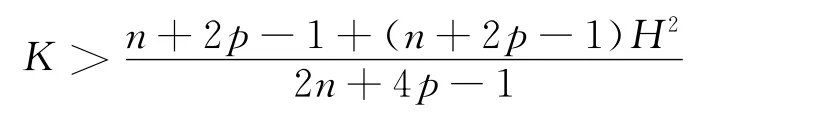
时，有S＝0，即Mn全测地.

另一方面，由文献［10］又有

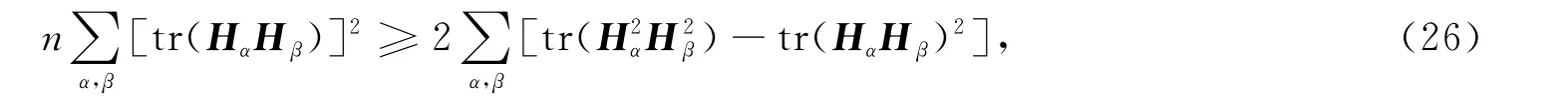
由式（19），（21），（26）有

2.2 定理5的证明

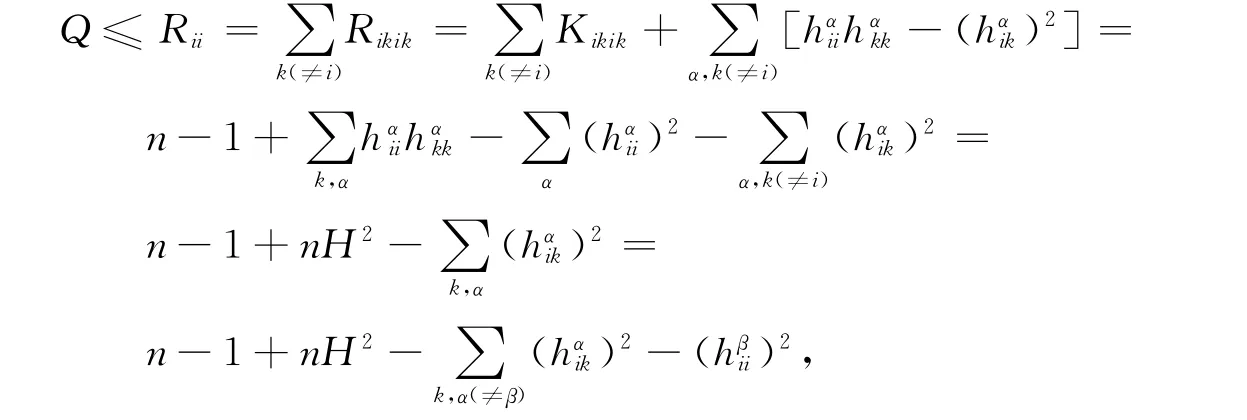
即

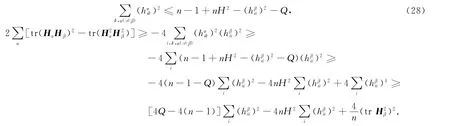
从而

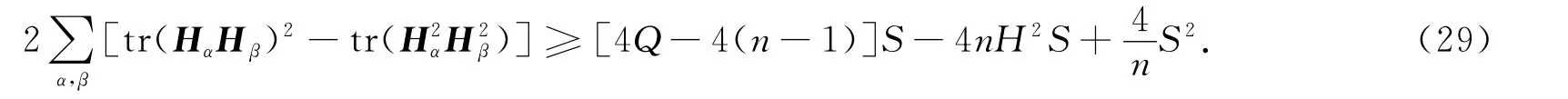
由式（13）有

在式（19）中取a＝－1，利用式（23），（24），（29），（30）有

将式（31）两边积分有

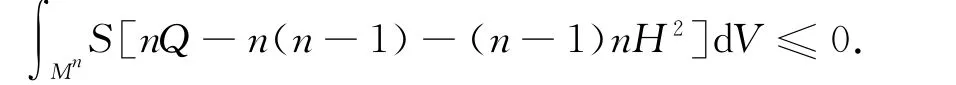
故当Q＞n－1＋（n－1）H2时，S＝0，即Mn全测地.

2.3 定理6的证明

在式（19）中取a＝－1，由引理3有

2.4 定理7的证明

由式（16）及文献［10］并结合H 为常数有

则

另一方面，由式（16）可得

由式（33），（34）得

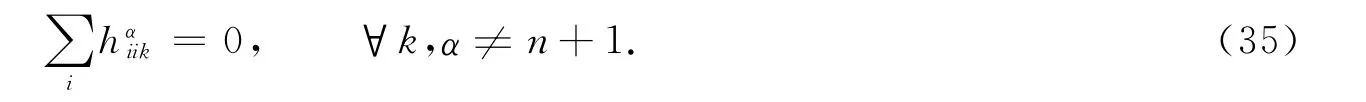
再结合式（32）的第一式有

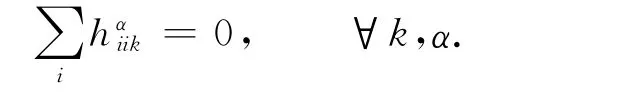
从而Mn具有平行平均曲率向量.

注3 由定理7知，关于CPn＋p中紧致具有常平均曲率的全实伪脐子流形研究可转化为紧致具有平行平均曲率向量的全实伪脐子流形的研究.

［1］WANG Hong.Several Global Pinching Theorem for Minimal Submanifolds in a Complex Projective Space［J］.Chinese Annals of Mathematics：Ser A，1991，12（3）：325－331.（王红.复射影空间中极小子流形的几个整体Pinching定理 ［J］.数学年刊：A辑，1991，12（3）：325－331.）

［2］ZHU Ye－cheng，SONG Wei－dong.2－Harmonic Submanifolds in a Complex Space Form ［J］.Journal of Mathematical Research ＆ Exposition，2008，28（3）：727－732.

［3］HU Xian－ju，WANG Li－juan，SONG Wei－dong.2－Harmonic Real Submanifolds in a Complex Projective Space［J］.College Mathematics，2009，25（1）：88－91.（胡显举，王丽娟，宋卫东.复射影空间中的2－调和全实子流形［J］.大学数学，2009，25（1）：88－91.）

［4］SHEN Yi－bing.Scalar Curvature of Totally Real Minimal Submanifolds ［J］.Chinese Annals of Mathematics：Ser A，1991，12（5）：573－577.（沈一兵.全实极小子流形的数量曲率 ［J］.数学年刊：A 辑，1991，12（5）：573－577.）

［5］SHEN Yi－bing.Totally Real Minimal Submanifolds in a Complex Projective Space ［J］.Journal of Scince，1983（3）：131－133.（沈一兵.复射影空间的全实极小子流形 ［J］.科学通报，1983（3）：131－133.）

［6］LI An－min，LI Ji－min.An Intrinsic Rigidity Theorem for Minimal Submanifolds in a Sphere［J］.Arch Math，1992，58（6）：582－594.

［7］ZHANG Liang.On Totally Real Pseudo－umbilical Submanifolds in a Complex Projective Space［J］.Journal of Math Research ＆ Exposition，2008，28（2）：421－428.

［8］Yau S T.Submanifolds with Constant Mean CurvatureⅡ ［J］.Amer J Math，1975，97（1）：76－100.

［9］纪永强.子流形几何 ［M］.北京：科学出版社，2004.

［10］Yau S T.Submanifolds with Constant Mean CurvatureⅠ ［J］.Amer J Math，1974，96（2）：346－366.