保线性算子q次数值域的线性映射

刘畔畔，张树功，李庆春

（1.吉林大学 数学研究所，长春130012；2.北华大学 数学与统计学院，吉林 吉林132013）

0 引言及预备知识

关于算子的数值域及广义数值域的研究目前已取得许多结果.Langer等［1］在研究定义于Hilbert空间上分块算子矩阵的谱理论过程中，首先引入了二次数值域的概念，但对它和数值域及谱的联系以及二次数值域的基本性质等未做深入探讨；文献［2］系统地研究了二次数值域与谱的关系，发现算子的二次数值域处于谱与数值域的闭包中；文献［3－4］将二次数值域推广到q次数值域，并得到了q次数值域的许多性质.刻画矩阵集之间保不变量线性算子的问题称为“线性保持问题”［5－11］，它在量子力学、微分几何、系统控制、数理统计等领域应用广泛.例如，当从一个系统过渡到另一个系统时，总是希望能保持某些性质和关系不变，这就要求引入线性保持问题.孙立宏［12］在一定条件下，刻画了保线性算子二次数值域线性映射的具体表示形式.本文探讨哪些线性算子在何种线性映射下保持q次数值域不变，讨论保线性算子q次数值域线性映射的一般形式，推广了文献［12］的结果.

其中Aij∈B（Hj，Hi），i，j＝1，2，…，q.

定义1 设Γ∈B（H），集合

定义1中，若q＝1，则W1（Γ）恰好是Γ的数值域；若q＝2，则W2（Γ）是文献［1－3，12］中Γ的二次数值域.为方便，下面假设H为n维Hilbert空间，Hi为ki维子空间，其上算子Aij∈B（Hj，Hi）在某一组基下的矩阵表示仍记为Aij.于是，Γ的矩阵表示仍记为Γ，可以表示为式（1），为说明对应的分块形式，简记为Γ（k）.

设Dn，Tn和Mn分别表示n×n复对角矩阵、复上三角矩阵和复矩阵代数.Dn（k），Tn（k）和Mn（k）分别表示q×q阶分块对角、分块上三角和分块矩阵类，其对角块是ki×ki（i＝1，2，…，q）阶矩阵，其中k＝（k1，k2，…，kq）T，k1＋k2＋…＋kq＝n.下面认为算子的线性映射即为矩阵类上的线性映射.

若线性映射Φ：Mn→Mn满足Wq（Γ）＝Wq（Φ（Γ）），∀Γ∈Mn，则称Φ为保线性算子q次数值域的线性映射.本文刻画线性映射Φ的表示形式.

1 主要结果

设Ci∈Mki（i＝1，2，…，q），定义C1⊕…⊕Cq＝diag（C1，…，Cq）.

引理1 设Ui（i＝1，2，…，q）是ki×ki阶酉矩阵，

则

其中U＊i（i＝1，2，…，q）是Ui的共轭转置.

证明：设λ∈Wq（Γ（k）），则存在xi∈ℂki，‖xi‖＝1，i＝1，2，…，q，使得

因为Ui（i＝1，2，…，q）是酉矩阵，设x′i＝Uixi，则‖x′i‖＝1（i＝1，2，…，q）.

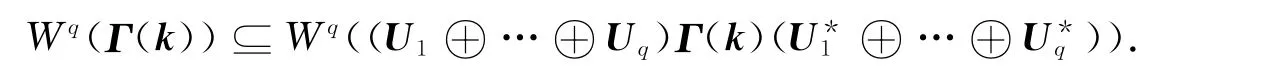
引理3［5，9］线性映射L：Mn→Mn是满射，则满足

的充要条件是存在酉矩阵U，使得L（A）＝UAU＊或L（A）＝（UAU＊）T，A∈Mn.

定理1 设ki＞1（i＝1，2，…，q），线性映射Φ：Tn（k）→Tn（k）满足：

且Φii：Mki→Mki（i＝1，2，…，q）是满射，则对任意的Γ（k）∈Tn（k），

成立的充要条件是存在酉矩阵Ui∈Mki（i＝1，2，…，q），使得

证明：充分性.由定理条件及引理2知式（2）成立，且

应用服务子系统为水利系统各类用户提供了查询应用水文气象各类产品的Web应用服务平台，采用了全新的Microsoft.NET体系结构，以ArcGIS10.0空间应用服务为WebGIS应用服务平台，以Microsoft的IE浏览器结合ArcGIS的SilverLight为用户应用终端，通过方便简捷的操作，将查询应用的各类水文气象产品以统一美观的风格展现给用户。应用服务子系统的用户包括水利部局域网用户、水利广域网用户和其他相关防汛部门的用户。

再由Φii（Aii）＝UiAiiU＊i或Φii（Aii）＝（UiAiiU＊i）T及引理3有W（Φii（Aii））＝W（Aii）（i＝1，2，…，q），从而充分性成立.

必要性.由式（2），（5）及必要性假设知

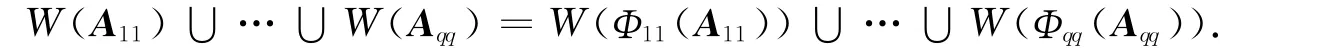
固定Aii＝0（i＝2，3，…，q），则由Φii（0）＝0（i＝2，3，…，q）得

即W（A11）∪｛0｝＝W（Φ11（A11））∪｛0｝.

注意到 W2（A11⊕0（n－k1）（n－k1））＝W （A11）∪ ｛0｝＝W （Φ11（A11））∪ ｛0｝， 由 文 献 ［2］知，W2（A11⊕0（n－k1）（n－k1））至多有两个连通分支组成，如果0∉W（A11），则必有0∉W（Φ11（A11））.从而对任意的A11∈Mk1，W（A11）＝W（Φ11（A11））成立.根据引理3，存在酉矩阵U1∈Mk1，使得Φ11（A11）＝U1A11U＊1或Φ11（A11）＝（U1A11U＊1）T.

同理可以证明存在酉矩阵Ui∈Mki（i＝2，3，…，q），使得式（4）成立.

推论1 设1＜ki＜∞（i＝1，2，…，q），线性映射Φ：Dn（k）→Dn（k）满足

且Φii：Mki→Mki（i＝1，2，…，q）是满射，则

成立的充要条件是存在酉矩阵Ui∈Mki（i＝1，2，…，q），使得式（4）成立.

定理2 设1＜ki＜∞（i＝1，2，…，q），k1＋k2＋…＋kq＝n.若Φ：Mn（k）→Mn（k）可表示为

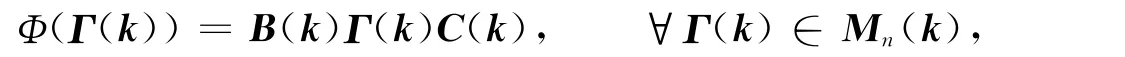
其中B（k），C（k）∈Mn（k），且满足

这里Φii：Mki→Mki（i＝1，2，…，q）是满射，Aii（i＝1，2，…，q）是对称矩阵，则对满足该条件的Γ（k）∈Mn（k），式（3）成立的充要条件是存在酉矩阵Ui∈Mki（i＝1，2，…，q），使得

且Φst（Ast）（s≠t）由Φii（Aii）唯一确定，即

也即B（k）＝diag（U1，…，Uq），C（k）＝B（k）＊.

证明：由引理1可知充分性成立.

下证必要性.取Ast＝0（s，t＝1，2，…，q，s≠t）和Aii＝λI（i＝2，3，…，q），则对任意的A11∈Mk1，由引理2得

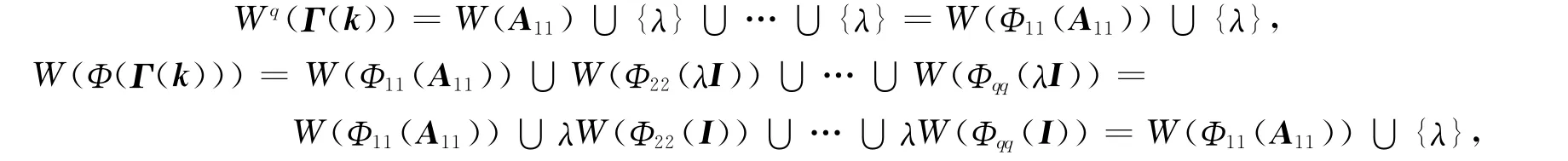
故

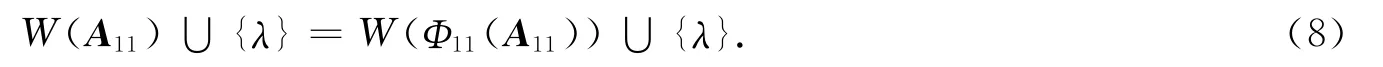
由式（8）知

注意到k1＞1，k2＞1，由文献［2］知二次数值域或者是连通集或者有两个连通分支，从而类似于定理1的证明可以推出W（A11）＝W（Φ11（A11））.

类似地，可以证明W（Aii）＝W（Φii（Aii））对任意的Aii∈Mki（i＝2，3，…，q）成立.

由引理3，存在酉矩阵Ui∈Mki（i＝1，2，…，q），使得式（4）成立.注意Φii（Aii）＝（UiAiiU＊i）T＝（U＊i）TAiiUTi，记Vi＝（U＊i）T，则Vi仍为酉矩阵，且V＊i＝UTi，仍记Vi为Ui，则式（6）成立.

根据定理的条件，可设

经计算得

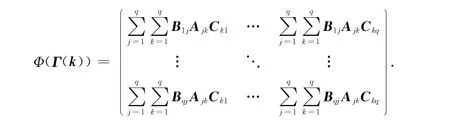
下面证明B＝diag（U1，…，Uq），C＝diag（U＊1，…，U＊q）.由于已证明Φii（Aii）＝UiAiiU＊i（i＝1，2，…，q），则由

取除Aii外的所有Ajk＝0（j，k＝1，2，…，q）及Aii的任意性，可得Bii＝Ui，Cii＝U＊i，i＝1，2，…，q.

对式（9），当i＝1时，若取除A12外所有的Aij＝0（i，j＝1，2，…，q）可得B11A12C21＝0，则由B11＝U1为酉矩阵知Ak1k2C21＝0，又由A12的任意性得C21＝0.若取除A13外所有的Aij＝0（i，j＝1，2，…，q）可得C31＝0.依此类推，可得到矩阵C的第1列除C11外均为0.同理可得到矩阵B的第1行除B11外均为0.

类似地，当i＝2，3，…，q时，对式（9）中的Aij取特殊值，则可得矩阵C的其他q－1列除C的对角元外均为0，以及矩阵B的其他q－1行除B的对角元外均为0，从而B＝diag（U1，…，Uq），C＝diag（U＊1，…，U＊q）.即式（7）成立.

定理3 若线性映射Φ（Γ（k））＝Γ（k）T，则式（3）成立.

证明：设λ0∈Wq（Γ（k）T），则存在xi∈ℂki，‖xi‖＝1，i＝1，2，…，q，使得

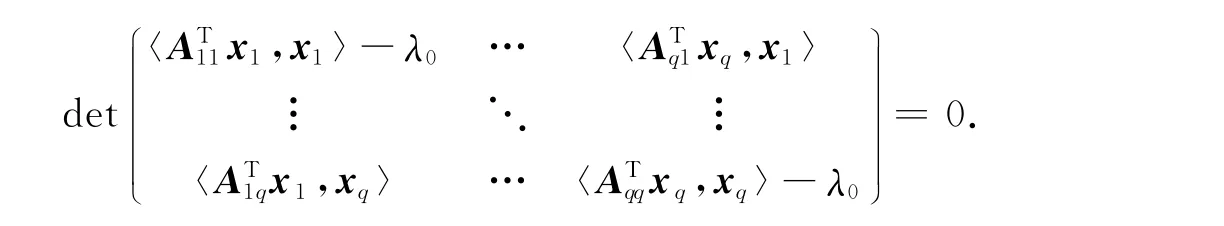
注意到

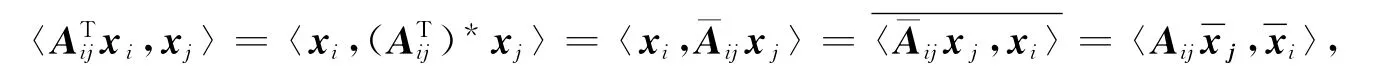
于是可得

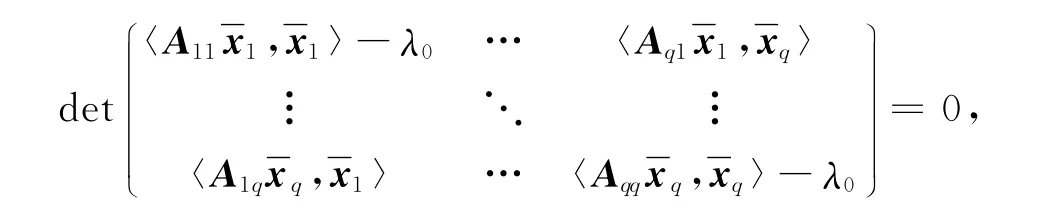
从而

即λ0∈Wq（Γ（k）），所以Wq（Φ（Γ（k）））⊆Wq（Γ（k））.

类似可证Wq（Γ（k））⊆Wq（Φ（Γ（k）））.

［1］Langer H，Tretter C.Spectral Decomposition of Some Nonselfadjoint Block Operator Matrices［J］.Journal of Operator Theory，1998，39：339－359.

［2］Langer H，Markus A，Matsaev V，et al.A New Concept for Block Operator Matrices：The Quadratic Numerical Range［J］.Linear Algebra and Its Application，2001，330（1／2／3）：89－112.

［3］Tretter C，Wagenhofer M.The Block Numerical Range of an n×n Block Operator Matrix［J］.SIAM Journal on Matrix Analysis and Applications，2003，24：1003－1017.

［4］REN Fang－guo.Research on Operator Completions and Generalized Numerical Ranges of Operator［D］.Xi’an：Shaanxi Normal University，2004.（任芳国.关于算子补与广义数值域的研究 ［D］.西安：陕西师范大学，2004.）

［5］Li C K，Tsing N K.Linear Preserver Problems：A Brief Introduction and Some Special Techniques［J］.Linear Algebra and Its Application，1992，162／163／164：217－235.

［6］Burgos M.Orthogonality Preserving Linear Maps on C＊－Algebras with Non－zero Socles ［J］.Journal of Mathematical Analysis and Applications，2013，401（2）：479－487.

［7］Pazzis C S.The Linear Preservers of Non－singularity in a Large Space of Matrices［J］.Linear Algebra and Its Application，2012，436（9）：3507－3530.

［8］JI Guo－xing，WU Bao－wei.Similarity Preserving Linear Maps on Upper Triangular Matrix Algebras［J］.Linear Algebra and Its Application，2006，414（1）：278－287.

［9］Omladic M.On Operators Preserving the Numerical Range［J］.Linear Algebra and Its Application，1990，134：31－51.

［10］TANG Xiao－min，YANG Ya－qin.Strong Linear Preservers of Rank Reverse Permutability on Triangular Matrices［J］.Linear Algebra and Its Application，2006，414（1）：84－96.

［11］Rodam L，Šemrl P.A Localization Technique for Linear Preserver Problems ［J］.Linear Algebra and Its Application，2010，433（11／12）：2257－2268.

［12］SUN Li－hong.The Quadratic Numerical Range of Block Operator Matrices and the Linear Maps Preserving the Quadratic Numerical Range［D］.Qingdao：Qingdao University of Science and Technology，2009.（孙立宏.块算子矩阵二次数值值域及保二次数值值域的线性映射 ［D］.青岛：青岛科技大学，2009.）