旋转矢量法在简谐振动和简谐波问题求解中的应用

樊丽娟，冯云光

（ 铜仁学院 物理与应用工程系，贵州 铜仁 554300 ）

在大学物理课程中，求解简谐振动和简谐波的问题一直是学生学习的难点，究其原因，关键是求初相位时遇到困难。教学中，常用两种方法即解析分析法（由位置坐标和速度的初始条件求初相位）和旋转矢量图示法求初相位，但解析法需要较麻烦的推理过程，学生在求解时常常出现错误，而旋转矢量法充分利用了大家熟悉的几何、三角知识，利用它对简谐振动过程的形象、直观的分析，使求解简谐振动问题变得十分简洁、方便。

1．简谐振动

可以用单一频率的谐函数来描述的振动称为简谐振动。它是周期振动的一种简单形式。典型的简谐振动有弹簧振子、单摆、复摆和扭摆等。在忽略阻尼的理想情况下，它们有共同的运动规律。例如，弹簧振子和扭摆在弹簧的线性范围内的运动；单摆和复摆在小振幅时的运动。描述它们的振动的动力学方程为：

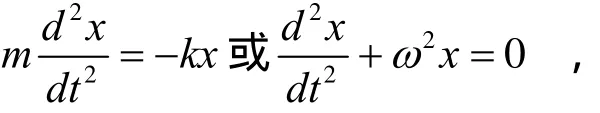
2．简谐振动的旋转矢量表示法

图1 简谐振动的旋转矢量表示示意图

如图 1所示，简谐振动 x = Acos(ω t+ φ )可以用一个质点M在以圆心为O，半径为A的圆周上作匀角速度运动来描述。该圆的半径等于简谐振动的振幅A，M点的角速度ω为振动的圆频率。在 t = 0 时刻，与x轴夹角φ为简谐振动的初相，在时刻 t时，■与x轴的夹角为该时刻的相位角ωt+φ ，在x轴上的投影即为该时刻的振动位移。根据上述分析，显然可以用矢量来代表质点 M 在 x方向的简谐振动[1]，矢量称为旋转矢量。需要注意的是，作简谐振动的并非旋转矢量本身，而是它的矢端在x轴上的投影点在x轴上做简谐振动，并且描述简谐振动的特征量Aωφ、、不真正具有旋转矢量图中所赋予它们的几何意义，这些几何关系只是为了形象、直观地描述简谐振动而引入的。

3．旋转矢量法应用例析

旋转矢量法可以十分直观地描述简谐振动表达式中的A,ω和φ,尤其求初相位和相位差，并为讨论简谐振动的合成提供简便的方法。下面仅以几例说明旋转矢量法在简谐振动中的运用。

3．1． 用旋转矢量法求初相位和比较相位差[2]

例1 一放置在水平桌面上的弹簧振子，当 0t=时，（1）物体在正方向的端点；（2）物体在平衡位置，向负方向运动；（3）物体在正二分之一振幅处，向负方向运动；（4）物体在负二分之一振幅处，向正方向运动。求以上各种情况的初相位。

解：用旋转矢量法分别画出四个不同初始状态的旋转矢量图，如图 2所示。它们所对应的初相位分别为

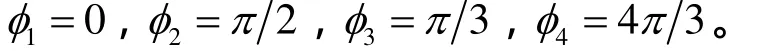
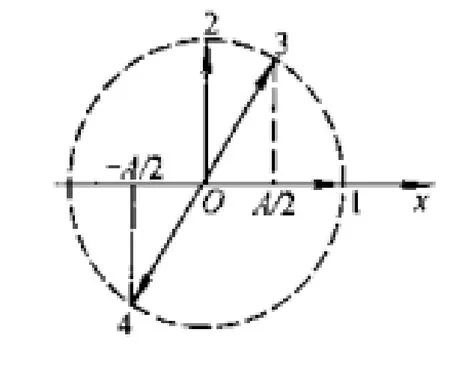
图2 不同初始状态的旋转矢量图

例 2 一平面简谐波沿x轴负方向传播，角频率为ω，设 /4tT= 时刻的波形图如图3（a）所示，则该波的初相位为多少？

分析与解：用旋转矢量法求出波动方程的初相位。由图3（a）可知 t = T /4时原点处质点的位移为0，且向y轴正方向运动，则此时刻旋转矢量图如图3（b）所示。要求初相位，只要将该时刻的旋转矢量反转（顺时针转） Δ φ=ω· T /4 = π/2，即得φ0=π。

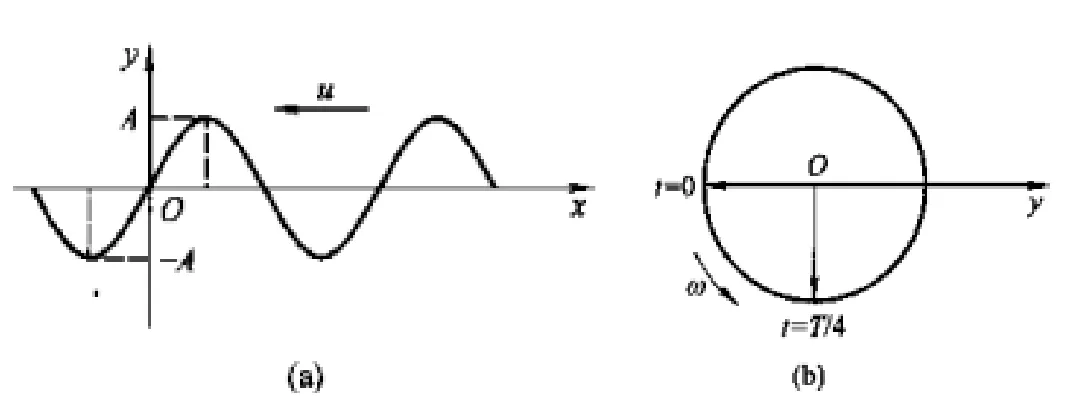
图3 平面简谐波的波形图与旋转矢量图

例3 两个同周期的简谐运动曲线如图4（a）所示，分析1x的相位与2x的相位之差。

分析与解：由振动曲线图作出相应的旋转矢量图，如图4（b）所示，即可得到答案：1x的相位比2x的相位超前/2π。

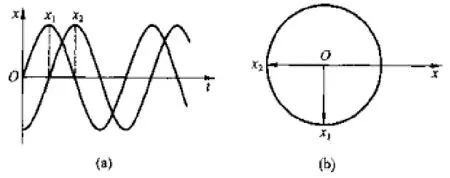
图4 同周期的简谐运动振动曲线图和旋转矢量图

3．2． 用旋转矢量法求简谐振动物体任意两个状态间所用的时间

例 4 作简谐运动的物体由平衡位置向x轴正向运动，试问经过下列路程所需的最短时间各为周期的几分之几？（1）由平衡位置到最大位移处；（2）由平衡位置到 /2A 处；（3）由 /2A 处到最大位移处。

解：采用旋转矢量法求解较为方便。按题意作如图5所示的旋转矢量图，平衡位置在O点。

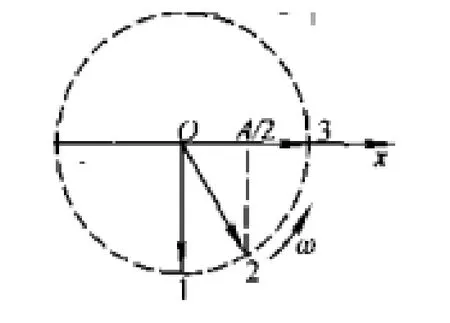
图5 简谐运动物体不同状态的旋转矢量图

（1）由平衡位置到最大位移处，对应于图中的旋转矢量从位置1到位置3，故 Δ φ1= π /2，则所需时间间隔： Δ t1=Δφ1/ω = T /4。

（2）由平衡位置到 A / 2处，对应于图中旋转矢量从位置1到位置2，有 Δ φ2= π /6，则所需时间：。

（3）由 A / 2处到最大位移处，对应于图中旋转矢量从位置2到位置3，有 Δ φ3= π /3，则所需时间：Δt3=Δφ3/ω = T /6。

3．3．由已知简谐运动的x t-图或旋转矢量图作出另一图线

例5 如图6所示，右方表示某简谐运动的x t- 图线，试用作图方法画出1t时刻和2t时刻的旋转矢量的位置[3]。

图6 简谐运动的x-t图（右）与旋转矢量图（左）

解：量出振幅并以此为半径画圆，如图6左方，画x轴通过圆心，且垂直于t轴，过 t1和 t2作与x轴平行的直线交曲线于 P1和 P2。过 P1画■与t轴平行的直线交圆周于A、A′两点， 、 ′在 x轴上的投影似乎均等于 t1时刻的位移，谁是所求的旋转矢量？因 P1处曲线的斜率为负，即速度为负，表■■示■此时质点速度与x轴方向相反，故旋转■■矢■量应在OA ，与此相似， t2时刻旋转矢量运动至OB 。

同样的方法，可由旋转矢量图画出简谐运动的x - t图线。

例6 一简谐振动的运动方程为 x = A cos(ω t+ φ )，设 φ =π/4，试利用旋转矢量绘出它的x-t图[4]。

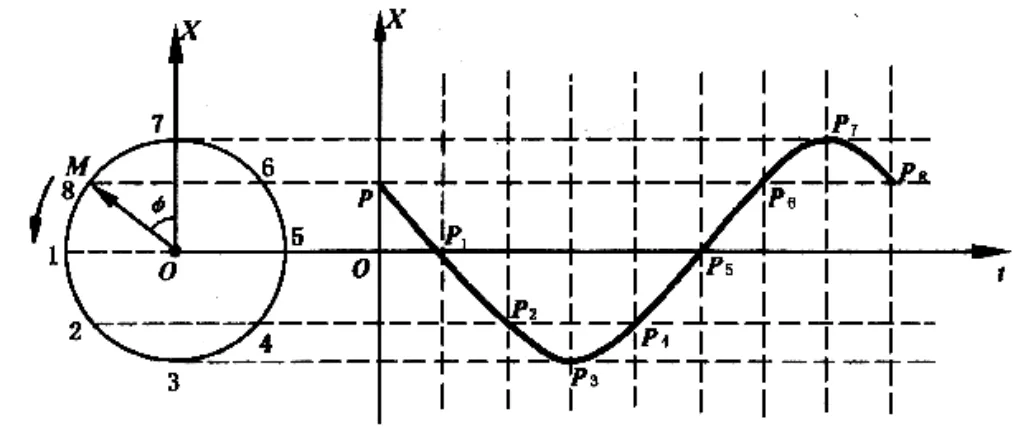
图7 简谐运动的旋转矢量图（左）与x-t图（右）

3．4．应用比较相位法求波动方程

当一列平面简谐波沿x轴传播时，波线上各处介质元除振动不同外，其它振动参量都相同。故掌握波线上任意两处质元振动相位关系后，可由一处质元的振动方程写出其它各处质元的振动方程，进而可写出平面简谐波的波方程。

例 7 如图 8所示，一平面简谐波以速度u = 2 0m·s-1沿直线传播，已知在传播路径上某点A的简谐运动方程为 y =3× 1 0-2cos(4π t+ φ )，在 t =0时，该处质点位于正最大位移处。

（1）以点A为坐标原点，写出波动方程；

（2）以距点A为5m处的点B为坐标原点，写出波动方程。

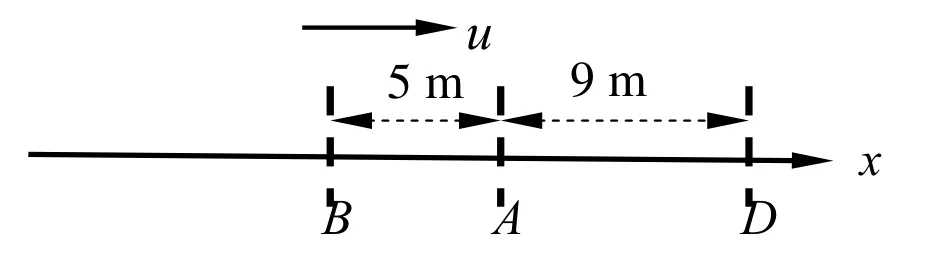
图8 平面简谐波沿直线传播示意图

解：由题意可知，在 t = 0 时，该处质点位于正最大位移处，由旋转矢量法很快得知初相位φ=0。由A的简谐运动方程可知

（1）以A为原点的波动方程为

（2）由于波由左向右行进，故点B的相位比点A超前，其简谐运动方程为：

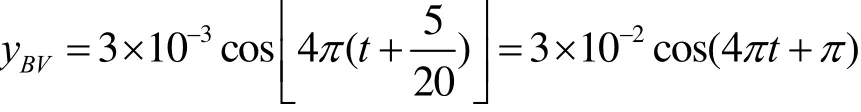
故以B为原点的波动方程为

旋转矢量法还可用于分析简谐振动的合成，例如求同方向同频率简谐振动的合成时，一般可代合振动振幅和初相公式，由初相公式求合振动初相φ时，会得到两个解，为最终确定φ所在的象限，仍应借助旋转矢量图。如果两分振动的相位差为特殊角（如0ππ、、/2等），则直接由旋转矢量法求合振动的Aφ、会更方便些。

4．结论

任何形式的简谐振动都可以用旋转矢量法来方便的描述，以上几个例子仅是教学中的实例。由于旋转矢量法对简谐运动过程的形象化分析，使简谐运动问题的处理变得十分简洁、方便，教学中学生易懂、易掌握，充分显示了该方法化难为易、妙用无穷的优越性。因此，旋转矢量法是解决简谐运动问题的便捷有效的工具。

[1]徐龙道，等．物理学词典[M]．北京：科学出版社，2004，5：116．

[2]马文蔚，等．物理学（第5版）下册[M]．北京：高等教育出版社，2006，3：39，88，39，53．

[3]漆安慎，杜婵英．力学（第2版）[M]．北京：高等教育出版社，2005，6：295．

[4]祝之光．物理学（下册）[M]．北京：高等教育出版社，2006，11：400．