裂缝性油气藏压裂水平井试井分析

姚 军，刘丕养，吴明录

(中国石油大学石油工程学院，山东青岛 266580)

非常规油气藏，如低渗油藏及页岩气藏，都普遍有微裂缝发育，属于裂缝性油气藏［1-2］。对于这些油气藏，水平井分段压裂开发是经济有效的方法之一［3-6］。Giger［7］首先提出水平井压裂问题并研究了低渗透油藏中压裂水平井的渗流场及压降分布规律［8］。Guo 和 Evans［9-12］利用实空间的点源函数和Newmann乘积原理得到了有多条裂缝的水平井压力动态解析解。Rbeawi［13］运用 Green函数法求出了均质油藏中具有多条倾斜裂缝压裂水平井的压力分布。1991年Ozkan［14］给出了拉氏空间内广泛的试井模型，考虑了不同的井类型、边界类型、均质或双重孔隙介质油藏类型。Raghavan等［15］利用盒状油藏拉氏空间点源解，采用叠加原理得到了多条横向裂缝压裂水平井拉氏空间解。Brown等［16］于2009年提出利用三线性流模型研究非常规油气藏的压裂水平井动态，该模型简单，计算方便，但无法准确表征压裂水平井各个流动阶段。在引用国外先进的试井技术的基础上，中国工作者提出了一些适用于中国油田的压裂水平井试井技术。李笑萍［17］讨论了具有多条裂缝的压裂水平井试井分析问题。刘振宇［18］研究了水平井穿越多条裂缝条件下的渗流规律以及裂缝的优化问题，并对压裂水平井与压裂直井的产能进行了比较分析。李军诗［19］对三维压裂水平井流动进行了简化，建立了有限导流压裂水平井非稳定渗流系统模型。笔者将有裂缝发育的介质看作双重介质，在Ozkan基本点源解的基础上，推导出不同边界条件下裂缝性油气藏分段压裂水平井单条及多条裂缝生产时的井底无因次压降求解公式，划分地下流体的流动形态，分析油藏边界及裂缝参数对压力动态的影响。

1 试井解释模型的建立及求解

1.1 物理模型

在实际的裂缝－孔隙性双重介质油气藏中，裂缝和基质岩块的分布是杂乱无章的，用常规的数学方法很难描述流体在其中的运动规律。为了研究的需要，本文采用Warren-Root模型描述实际的裂缝性油藏。Warren-Root模型认为，流体只能通过裂缝流向井筒，忽略基岩系统的向井流，但在基岩与裂缝系统之间存在窜流，这种模型称为双孔单渗模型。

水平井穿过多条裂缝的模型示意图如图1所示。假设油藏为双重介质油藏，地层各向异性，水平等厚，顶底封闭，考虑三种不同的外边界情况:无限大、封闭及定压;水平井仅在裂缝交界处射孔;水平井井底总流量固定，各条压裂裂缝的流量可以不相等;流体在水平井井筒及压裂裂缝内的流动均为无限导流;地层和流体微可压缩，且压缩系数为常数;流体为单相，且在地层中基岩和裂缝系统中的流动均符合达西定律;不考虑重力和毛管力的影响，并假设地层中的压力梯度较小。

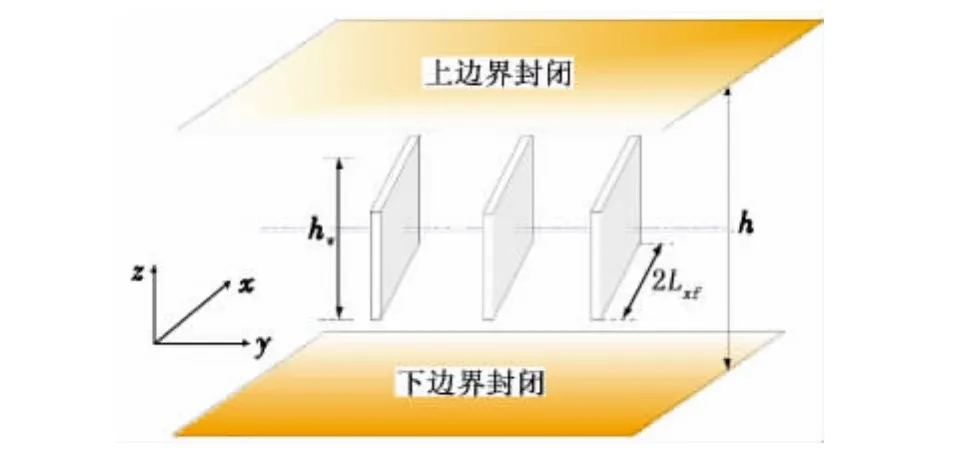
图1 水平井穿过多条裂缝示意图Fig.1 Sketch map of horizontal well intersected by multiple fractures

1.2 压裂水平井井底压力解

为了统一和简便，将各变量变换成无因次变量进行相关的计算和研究，各无因次参数定义如下:

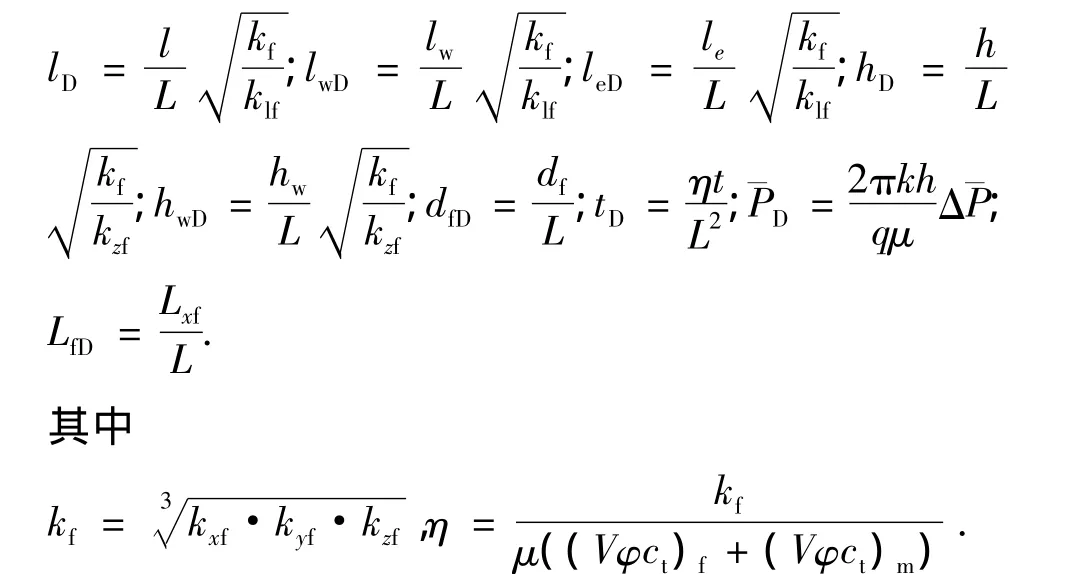
式中，l表示 x、y、z方向;kf为裂缝系统渗透率，μm2;h为油藏厚度，m;hw为压裂裂缝宽度，m;df为压裂裂缝间距，m;t为时间，s;P 为压力，10－1MPa;Lxf为压裂裂缝半长，m;L为参考长度，m;μ为渗流流体黏度，mPa·s;φ 为孔隙度;ct为综合压缩系数，MPa－1;下标D表示无因次量，下标f表示裂缝系统，下标m表示基岩系统，下标w表示压裂裂缝，下标e表示油藏边界。

1.2.1 单条裂缝时井底压力解

Ozkan［14］给出的双重介质顶底封闭四周无限大油藏的点源解为

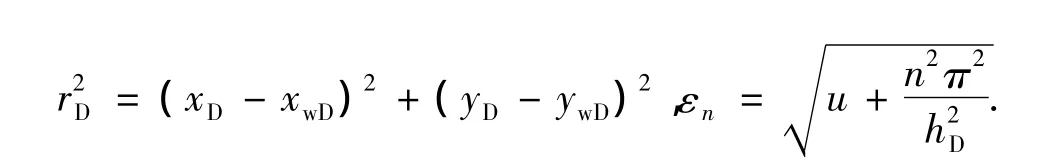
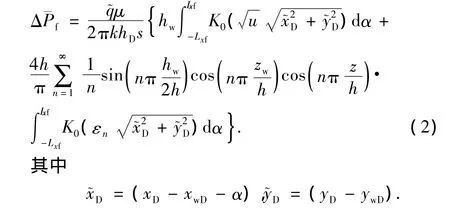
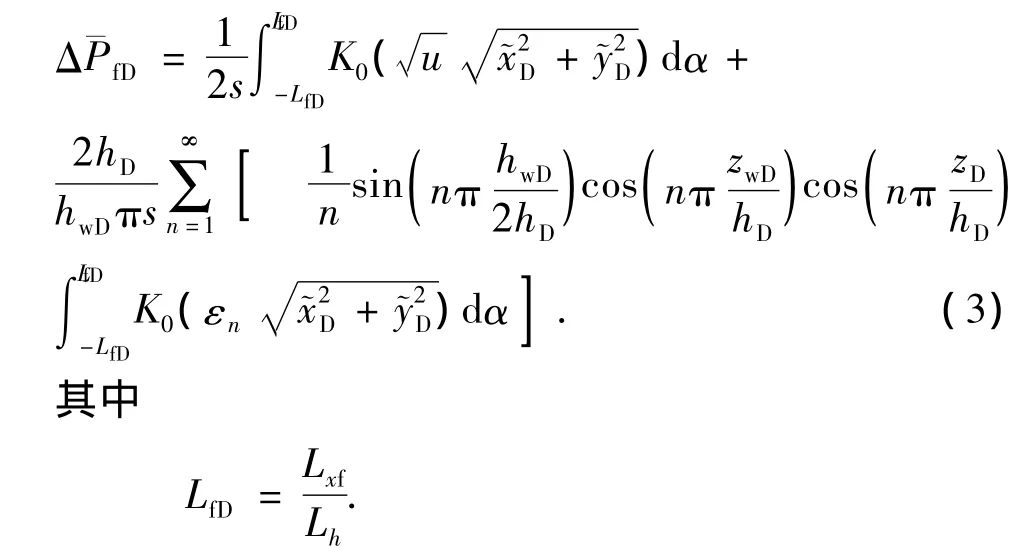
式(3)即为顶底封闭四周无限大油藏中长为2Lxf、宽为hw的单条压裂裂缝生产时，地层中任意一点在拉氏空间中的压降解。同理，可以得到盒状封闭油藏中一条不完全穿透地层压裂裂缝的压降解为

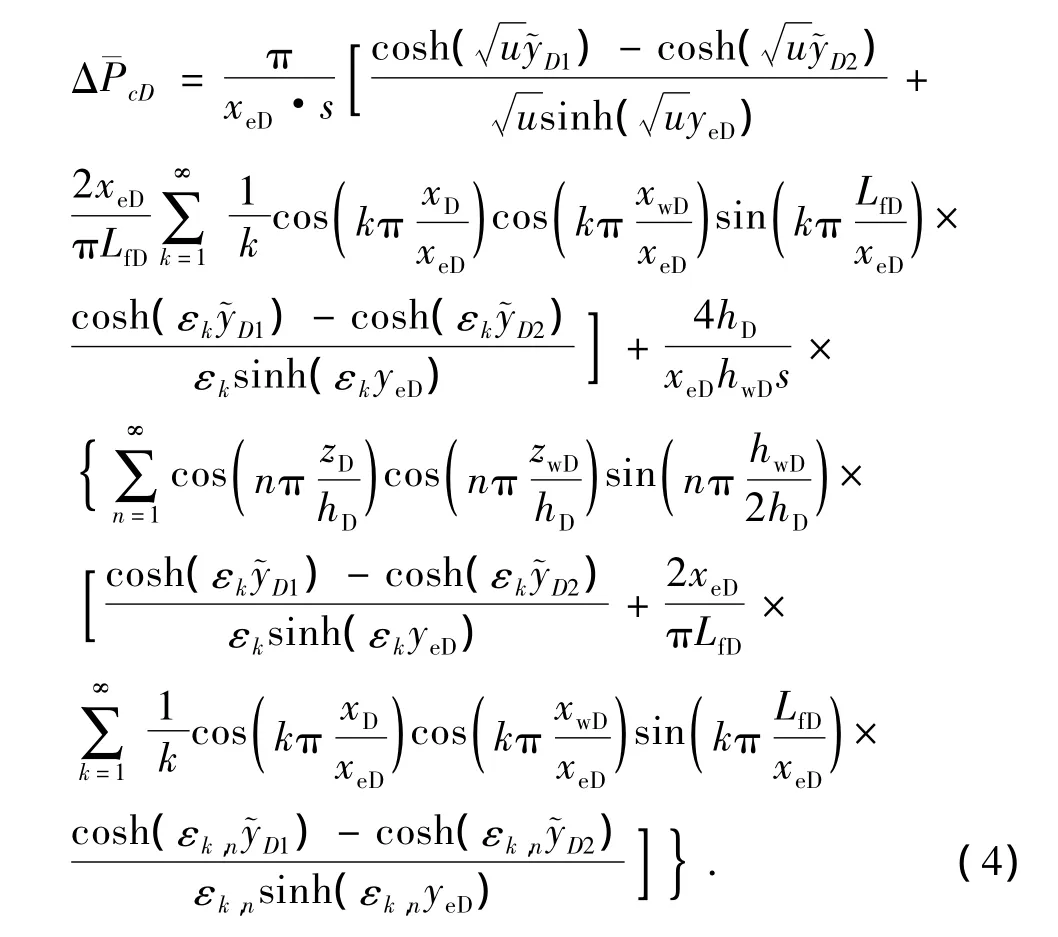
顶底封闭，四周定压的矩形油藏中一条不完全穿透地层压裂裂缝压降解为

1.2.2 多条裂缝时井底压力解

在数学模型中，假设压裂的裂缝条数为n，每一条压裂裂缝都假定拥有不同的特性，并且可以在井筒的任意位置。认为压裂裂缝都在相同的井筒压力下生产，即为水平井无限导流能力模型。压裂裂缝可以是横向的或者与井筒垂直。水平井总的流量是每一条压裂裂缝中流出流量的总和，用公式表示为

因此，无因次压力差可以通过褶积积分来求得，即

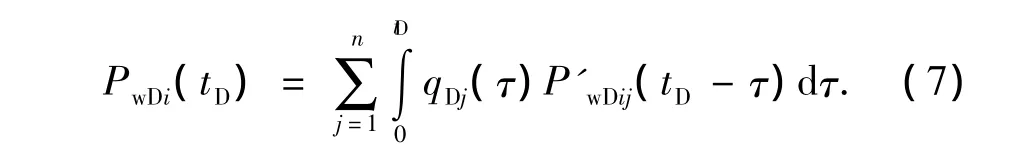
式中，PwDi表示微元i处的无因次压力差，PwDij表示由第j(j=1，2，…，n)条裂缝生产时在第i条裂缝处产生的压力差。

对式(6)和(7)进行Laplace变换，得

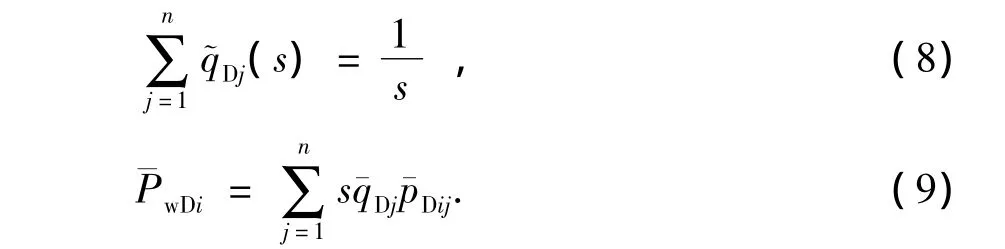
在无限导流能力的假设条件下，水平井井筒中各处保持相等的压力，可以表示为

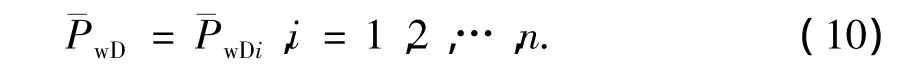
写出每条压裂裂缝上相应的公式(8)、(9)、(10)的形式，可以得到如下的矩阵方程组:

通过求解该矩阵方程组，可以求得井底压力解及每条裂缝的产量变化［20］。

1.3 考虑井筒存储和表皮效应时水平井井底压力的计算方法

上述计算的水平井井底压力并没有考虑井筒存储和污染的影响。在Laplace空间利用Duhamel原理，引入无因次井筒存储系数CD和总表皮系数S，得到Laplace空间压力解的关系［21］如下:

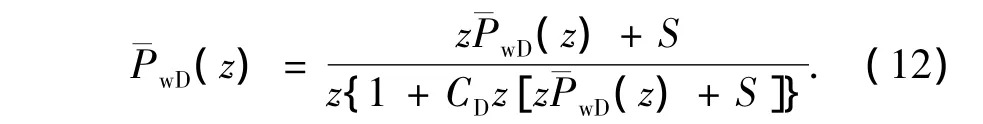
在Laplace空间计算得到水平井井底压力之后，再利用Stehfest数值反演方法［22］，便可得到真实空间内考虑井筒存储效应和表皮系数的压力pD。

2 压力动态分析

假设水平井存在3条垂直压裂裂缝，水平井交于裂缝中心。各无因次参数取值为:压裂裂缝半长LfD=0.2，压裂裂缝宽度hwD=0.1，水平井长度Lh=1，油藏长度xeD=12，油藏宽度yeD=12，油藏厚度hD=0.1，裂缝系统弹性储能比ω=0.1，窜流因子λ=0.1，井储系数 CD=10－5，表皮系数 S=0.01。

将裂缝性油藏看作双重介质油藏，与单重介质油藏相比存在基岩系统向裂缝系统的窜流，这在压力导数曲线上表现为一个“凹子”，如图2所示，“凹子”的深度与位置跟裂缝系统的弹性储能比及介质内部窜流系数有关。

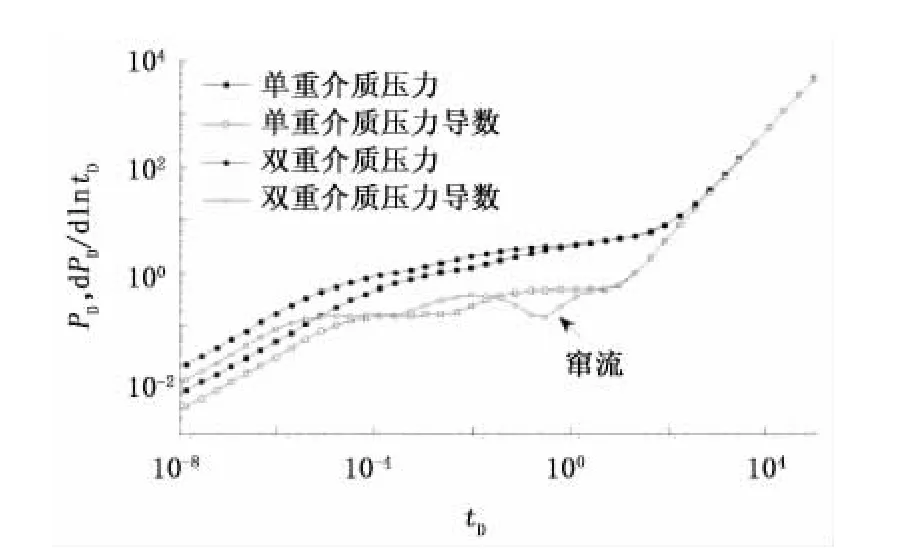
图2 不同介质类型压裂水平井压力动态对比Fig.2 Comparison of pressure behavior of fracturing horizontal well in different media

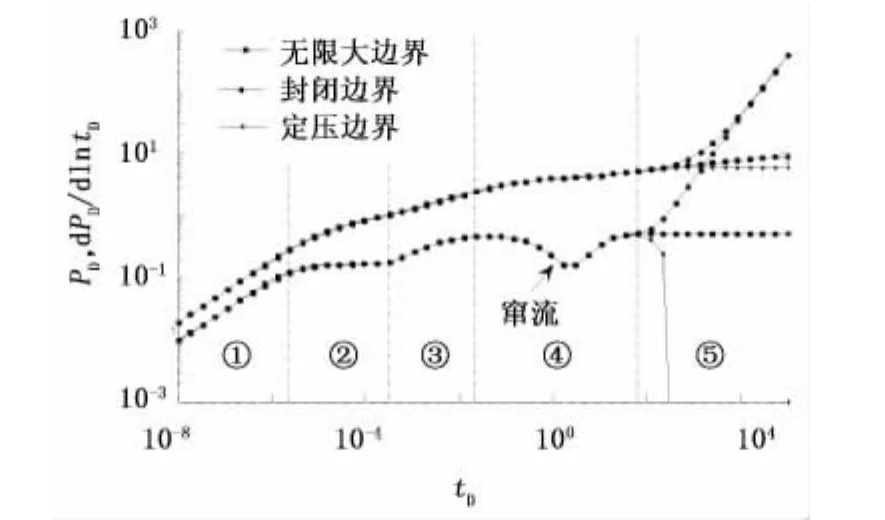
图3 不考虑井储和表皮的压裂水平井井底压力动态曲线Fig.3 Pressure behavior of fracturing horizontal well neglecting storage and skin factor

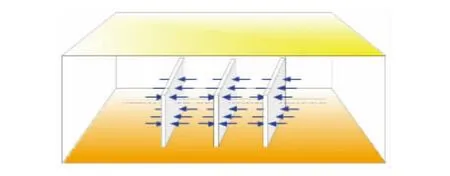
图4 裂缝线性流示意图Fig.4 Sketch map of fracturing lineal flow

如图3所示，不考虑水平井的井筒储存及表皮系数时，裂缝性油气藏压裂水平井的流动形态分为5种:①压裂裂缝线性流(图4)，是指在流动初期地层中流体线性的流向各条压裂裂缝。在双对数图上表现为无因次压力导数曲线为1/2斜率的直线段。②压裂裂缝径向流(图5)，是指若压裂裂缝较短，且缝距较大，则在各压裂裂缝周围产生水平径向流动，反之，该流动阶段不会出现。该流动段在双对数诊断图上表现为无因次压力导数曲线为一水平直线段。③地层线性流(图6)，是指在流动中后期，若边界较远，产生的流线相互平行，且垂直于水平井轴线的线性流动。该流动段的无因次压力导数曲线在双对数图上为1/2斜率的直线段。④系统径向流(图7)，是指对于整个油藏，如果生产时间很长，且压力波未传播到边界，则流体以拟径向流的形式向水平井及压裂裂缝区域流动。该流动段在双对数诊断图上表现为无因次压力导数曲线为0.5值水平直线段。⑤边界影响，是指压力波传播到边界以后，边界的性质对流体流动状态的影响。如果油藏具有封闭外边界，地层中出现拟稳态流动，双对数诊断图上表现为无因次压力导数曲线上翘并与无因次压力曲线重合;如果油藏具有定压外边界，则地层中压力趋于稳定，形成稳态，双对数诊断图上表现为无因次压力导数曲线急剧下掉，无因次压力曲线为水平线;如果油藏为无限大边界，则地层中流体继续系统径向流。

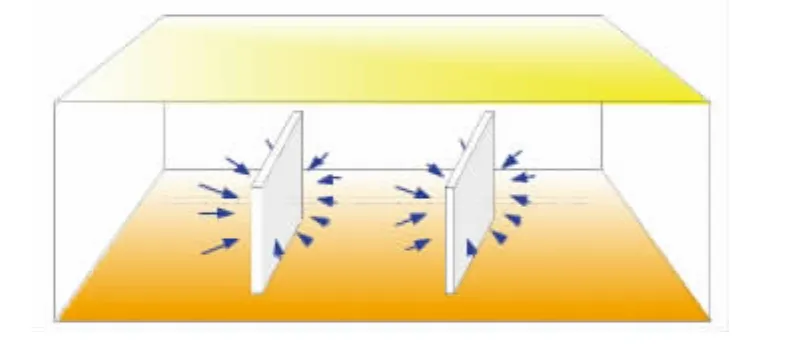
图5 裂缝径向流示意图Fig.5 Sketch map of fracturing radial flow

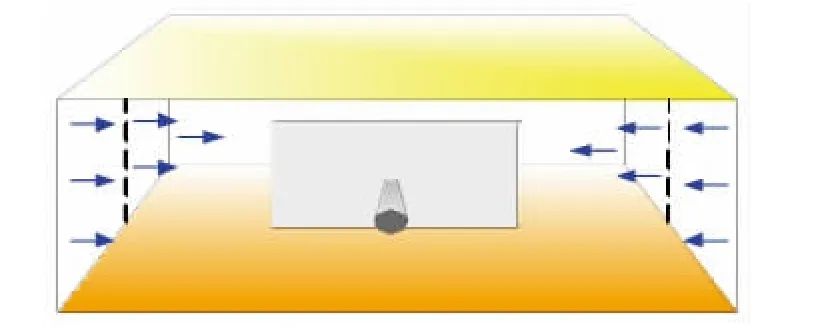
图6 地层线性流示意图Fig.6 Sketch map of formation lineal flow

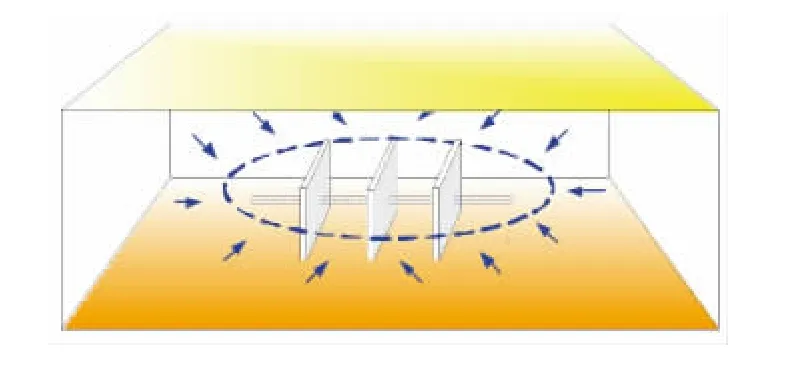
图7 系统径向流示意图Fig.7 Sketch map of formation radial flow

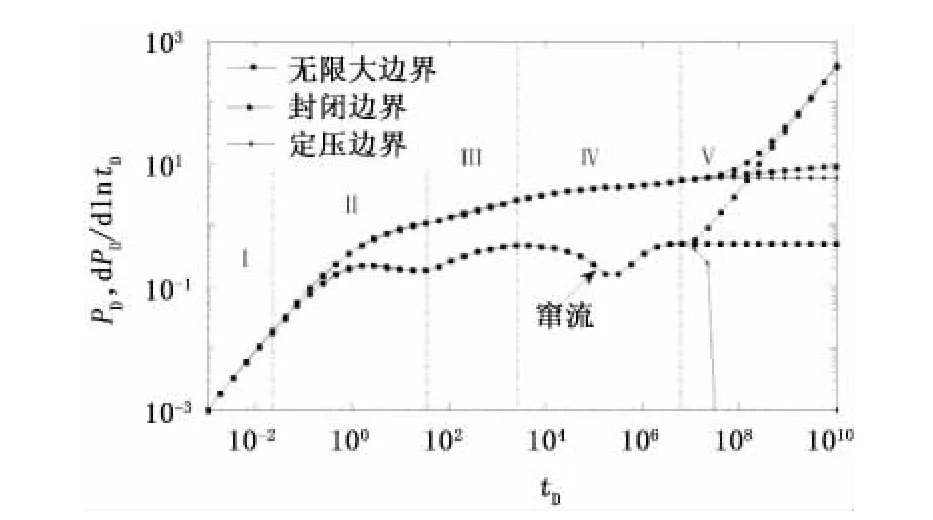
图8 考虑井储和表皮的压裂水平井井底压力动态曲线Fig.8 Pressure behavior of fracturing horizontal well considering storage and skin factor

如图8所示，考虑水平井井筒存储和表皮系数的影响时，井筒的续流段(图8中的Ⅰ区)和过渡段(图8中的Ⅱ区)掩盖了裂缝线性流和裂缝径向流阶段，Ⅲ、Ⅳ、Ⅴ区分别对应于图3中③ 、④ 、⑤ 区的流动阶段。如果井筒存储系数更大或表皮系数增大，续流段和过渡段甚至还会掩盖地层线性流阶段，所以实测的压力曲线中可能观察不到裂缝早期的流动形态。

3 参数敏感性分析

不同的油藏参数、压裂裂缝参数及井参数都会对水平井井底压力动态产生影响。以盒状封闭油藏中心一口压裂水平井生产的情况为例分析井底压力动态对各个参数的敏感性。

3.1 窜流系数对压力动态的影响

如图9所示，在双对数曲线图上可以看出，窜流出现在系统径向流阶段或流动达到边界以后，且窜流系数越大，窜流段出现的时间就越早，压力导数曲线上的“凹子”越靠近左侧。

图9 窜流系数对压裂水平井井底压力的影响Fig.9 Effect of interporosity flow on pressure behavior of fracturing horizontal well

3.2 弹性储能比对压力动态的影响

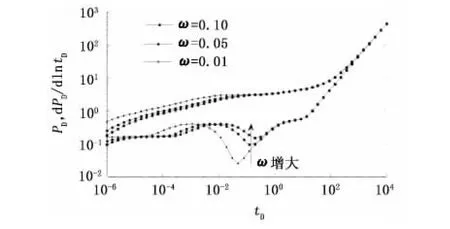
图10 弹性储能比对压力动态的影响Fig.10 Effect of storativity ratio on pressure behavior

如图10所示，弹性储容比ω对水平井井底压力动态的早期影响较大，ω越小，早期压降越大。这是因为ω表示的是裂缝系统的储油能力，早期流动主要是裂缝系统的流动。另外，ω的大小还决定了窜流持续的时间，ω越小，窜流持续的时间越长，在压力导数曲线上表现为“凹子”的深度越深、宽度越大。这是因为当裂缝系统压力降低后，基岩向裂缝补充流体，需要较长的时间才能提高裂缝系统的压力。

3.3 压裂裂缝条数对压力动态的影响

随着压裂工艺技术的不断完善，水平井可以采用分段压裂技术压出多条裂缝。由图11可知:压裂裂缝条数对压力动态曲线的影响较大，随着压裂裂缝条数的增加，同样的生产时间时，无因次井底压降变小。这是由于增大裂缝条数可以使流体更容易流入井底，从而减少了渗流的压力损失。但是随着裂缝条数的继续增加及生产时间的增加，这种效果会越来越不明显。由此可知，虽然裂缝条数较多能加快油藏的开发速度，但盲目增大裂缝条数会导致开采成本大幅度增长。对一具体油藏，存在一个最佳的裂缝条数值，在保证油藏高效开发的同时，获得最大的经济效益。

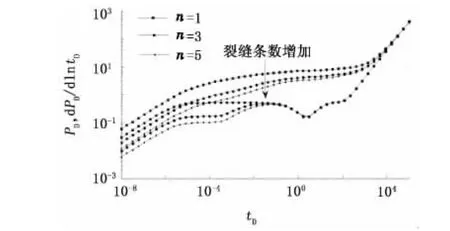
图11 裂缝条数nf对压裂水平井井底压力的影响Fig.11 Effect of fracture number on pressure behavior of fracturing horizontal wellbore

3.4 压裂裂缝半长对压力动态的影响

裂缝长度是影响压裂水平井生产动态的一个重要因素。图12为不同裂缝半长条件下的压力动态曲线。可以看出，随着裂缝长度的增加，无因次井底压降变小，但这种变小并不是无限制的。同时还可以观察到，压裂裂缝的长度会影响压裂裂缝径向流出现的时间。压裂裂缝越长，压裂裂缝径向流出现的时间越晚;当压裂裂缝很长时，压裂裂缝径向流将不会出现。

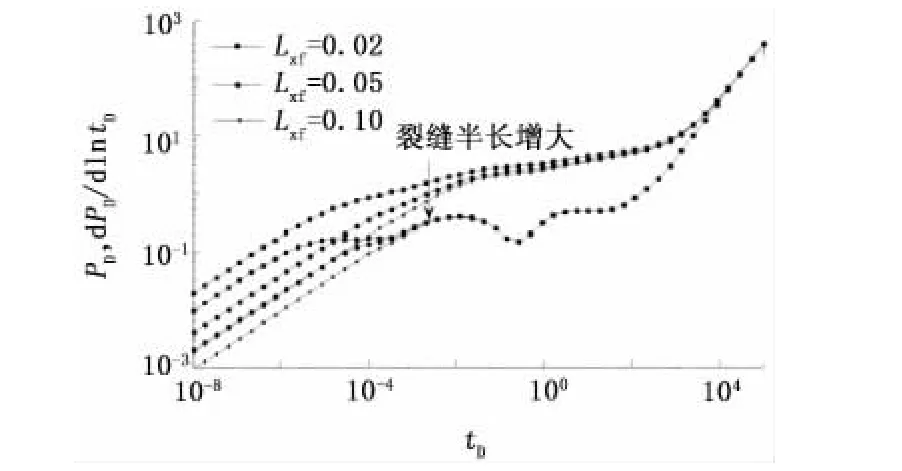
图12 裂缝半长Lxf对压裂水平井井底压力的影响Fig.12 Effect of fracture half-length on pressure behavior of fracturing horizontal wellbore

在纵向上增加裂缝长度即是增加裂缝宽度，研究发现，增加裂缝宽度对压力动态的影响与增加裂缝半长对压降的影响相同。这是因为不论是增加压裂裂缝的长度还是宽度都是增加了压裂缝的面积，从而使得流体更容易流向井筒，但裂缝宽度不会影响压裂裂缝径向流出现的时间。考虑到经济及技术因素，对于具体油藏来说，在裂缝条数、储层渗透率及裂缝导流能力等参数一定时，存在一个最优的裂缝长度及宽度。

3.5 压裂裂缝间距对压力动态的影响

如图13所示，从无因次压力导数曲线上可以看出，压裂裂缝间距会影响压裂裂缝径向流结束的时间，且缝距越小，压裂缝径向流持续的时间越短。这是因为当两条压裂裂缝靠近时，相互间的干扰作用就会加剧，使得两条裂缝中间形成一个低压区，低压区形成后，该区域的原油就很难流动，此时水平井的产量主要受裂缝外围区域流体渗流的影响。随着渗流区域的扩大，渗流阻力也会相应增加，与较大的裂缝间距相比，小的裂缝间距会使渗流在裂缝径向流结束后所需的压降变大，这一点在无因次压力曲线上可以看出。增大裂缝间距并不会增加施工难度及施工费用，同时裂缝间距的增大可以增加水平井周围的泄油面积，减小压裂裂缝间的相互干扰。因此，水平井压裂设计时应尽可能加大裂缝间距，以提高水平井压裂效益。

图13 裂缝间距d对压裂水平井井底压力的影响Fig.13 Effect of fracture spacing on pressure behavior of fracturing horizontal wellbore

4 实例验证

为验证模型的正确性，取某油田的一个测试实例进行验证。油藏的基础参数为:油层平均有效厚度32.5m，平均孔隙度0.2，井筒半径0.091 m，水平井水平段长度60 m，原油黏度2 mPa·s，原油体积系数 1.05，综合压缩系数 4.7 ×10－4MPa－1，测试前该井产量为60 m3/d。应用上述试井解释模型计算测试井的理论压力响应，并利用遗传算法对理论压力响应与实测压力响应进行自动拟合［23］，拟合结果如图14所示。由图14所示的压力恢复双对数拟合结果可得如下试井解释参数:平均渗透率k=180×10－3μm2，表皮系数 S=0，弹性储能比 ω =0.199，窜流系数λ=9.89×10－6，裂缝条数 n=3，裂缝半长Lxf=5.8 m。

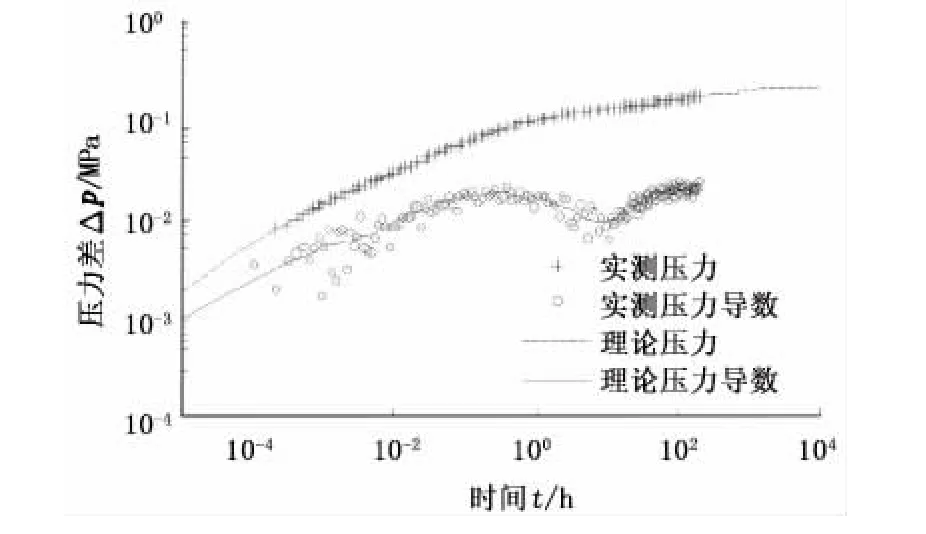
图14 测试井理论曲线与实测曲线双对数拟合图Fig.14 Type curve matching of theoretical curves and tested curves

5 结束语

利用Green函数法，通过镜像映射和叠加原理求得了顶底封闭四周无限大、封闭及定压边界条件下裂缝性油气藏压裂水平井单条裂缝或多条裂缝生产时水平井井底压力响应的Laplace空间解。裂缝性油气藏压裂水平井存在压裂裂缝线性流、压裂裂缝径向流、地层线性流、系统径向流及边界影响5种流动形态，并且会出现基岩系统向裂缝系统的窜流。压裂裂缝条数越多，相同的生产时间时，无因次井底压降越小，但当压力波传播到边界后，裂缝条数不再对流动造成明显影响;压裂裂缝长度及宽度只影响地层线性流之前的流动，增加压裂裂缝长度或宽度，无因次井底压降减小，且随着压裂裂缝长度的增加，压裂裂缝径向流出现的时间越来越晚，当压力裂缝长度很大时，压力裂缝径向流将不会出现;压裂裂缝间距会影响压裂裂缝径向流结束的时间，且缝距越小，压裂裂缝径向流持续的时间越短。现场应用实例证明了试井解释模型的正确性。

［1］ 黄延章.低渗透油层渗流机理［M］.北京:石油工业出版社，1998:58-79.

［2］ 姚军，孙海，樊冬艳，等.页岩气藏运移机制及数值模拟［J］.中国石油大学学报:自然科学版，2013，37(1):91-98.YAO Jun，SUN Hai，FAN Dong-yan，et al.Transport mechanisms and numerical simulation of shale gas reservoirs［J］.Journal of China University of Petroleum(Edition of Natural Science)，2013，37(1):91-98.

［3］ 李廷礼，李春兰，吴英，等.低渗透油藏压裂水平井产能计算新方法［J］.中国石油大学学报:自然科学版，2006，30(2):48-52.LI Ting-li，LI Chun-lan，WU Ying，et al.A new way to calculate fractured horizontal wells productivity in low permeability oil reservoirs［J］.Journal of China University of Petroleum(Edition of Natural Science)，2006，30(2):48-52.

［4］ NOBAKHT M，CLARKSON C.R，KAVIANINEW D.Type curves for analyzing horizontal well with multiple fractures in shale gas reservoirs［R］.SPE 149397，2011.

［5］ LEWIS A M，HUGHES R G.Production data analysis of shale gas reservoirs［R］.SPE 116688，2008.

［6］ IKEWUN P，AHMADI M.Production optimization and forecasting of shale gas wells using simulation models and decline curve analysis［R］.SPE 153914，2012.

［7］ GIGER F M.Horizontal wells production techniques in heterogeneous reservoirs［R］.SPE 13710，1985.

［8］ GIGER F M.Low-permeability reservoirs development using horizontal wells［R］.SPE 16406，1987.

［9］ GUO G L，EVANS R D.Pressure-transient behavior and inflow performance of horizontal wells intersecting discrete fractures［R］.SPE 26446，1993.

［10］ GUO G L，EVANS R D.Inflow performance and production forecasting of horizontal wells with multiple hydraulic fractures in low-permeability gas reservoirs［R］.SPE 26169，1993.

［11］ GUO G L，EVANS R D.Inflow performance of a horizontal well intersecting natural fractures［R］.SPE 25501，1993.

［12］ GUO G L，EVANS R D.Pressure-transient behavior for a horizontal well intersecting multiple random discrete fractures［R］.SPE 28390，1994.

［13］ RBEAWI S A，TIAB D.Transient pressure analysis of a horizontal well with multiple inclined hydraulic fractures using type-curve matching［R］.SPE 149902，2012.

［14］ OZKAN E，RAGHAVAN R.New solutions for well test analysisproblems:part1—analyticalconsiderations［R］.SPE 18615，1991.

［15］ RAGHAVAN R S，CHEN C C，AGARWAL B.An analysis of horizontal wells intercepted by multiple fractures［R］.SPE 27652，1997.

［16］ BROWN M，OZKAN E，RAGHAVAN R，et al.Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs［R］.SPE 125043，2009.

［17］ 李笑萍.穿过多条垂直裂缝的水平井渗流问题及压降曲线［J］.石油学报，1996，17(2):91-97.LI Xiao-ping.Fluid flow through pay zones in relation to drawdown profiles in a horizontal well intersecting several vertical fractures［J］.Acta Petrolei Sinica，1996，17(2):91-97.

［18］ 刘振宇，刘洋，贺丽艳，等.人工压裂水平井研究综述［J］.大庆石油学院学报，2002，26(4):96-99.LIU Zhen-yu，LIU Yang，HE Li-yan，et al.Overview of the research of hydraulically fractured horizontal wells［J］.Journal of Daqing Petroleum Institute，2002，26(4):96-99.

［19］ 李军诗.压裂水平井动态分析研究［D］.北京:中国地质大学(北京)地球科学与资源学院，2005.LI Jun-shi.A study of performance analysis of horizontal wells with a single or multiple fractures［D］.Beijing:School of Earth Sciences and resources，China University of Geosciences(Beijing)，2005.

［20］ ZERZAR A，BETTAM Y.Interpretation of multiple hydraulically fractured horizontal wells in closed systems［R］.SPE 84888，2003.

［21］ 姚军，李爱芬.单孔隙介质渗流问题的统一解［J］.水动力学研究与进展，1999，A辑，14(3):317-324.YAO Jun，LI Ai-fen.General solutions for seepage flow in single porous medium［J］.Journal of Hydrodynamics，1999，Ser A，14(3):317-324.

［22］ 同登科，陈钦雷.关于Laplace数值反演Stehfest方法的一点注记［J］.石油学报，2001，22(6):91-92.TONG Deng-ke，CHEN Qin-lei.Note on Stehfest method of Laplace numerical inversion［J］.Acta Petrolei Sinica，2001，22(6):91-92.

［23］ 吴明录，姚军，王子胜，等.利用双种群遗传算法进行数值试井自动拟合［J］.油气地质与采收率，2007，14(2):81-83.WU Ming-lu，YAO Jun，WANG Zi-sheng，et al.Numerical well testing auto-matching applying double population genetic algorithm［J］.PGRE，2007，14(2):81-83.