利用已钻井资料构建区域地层压力剖面的方法

管志川，魏 凯

(中国石油大学石油工程学院，山东青岛 266580)

在石油与天然气的钻探、开发设计与施工过程中，准确预测和掌握地层压力非常重要［1］。目前用于地层压力预测、监测和检测的方法很多，主要有地质分析法、地震法、dc指数法和测井法等［2］。地震资料是钻井之前能够获得的为数不多的资料之一，由地震资料进行地层孔隙压力预测在大多数情况下是无法替代的选择［3］。一旦一个区域内已经获得了一口或若干口已钻井的钻井或测井资料，如何向新的待钻井移植，使地层压力预测的精度更高，一直是研究人员关注的问题。一般情况下，工程人员采用直接地层对比的方法，将邻井的地层压力直接应用于新井中［4］。笔者针对这一问题，考虑目标地层的空间分布特性，提出地层压力矩阵的概念，给出建立包含地层埋深和压力信息的待钻井目标层段的地层压力矩阵的方法，为待钻井井身结构设计和钻井液密度设计所需基础数据的获取提供一种新的有效手段。

1 地层压力矩阵的建立

地层压力由于受地层的起伏、厚度变化、延伸趋势以及断层的影响，在区域的目标层段内变化较大，因此在利用附近已钻井的井筒资料预测待钻井地层压力时，需要充分考虑地层的空间展布及区域地质构造，定义包含地层埋深和压力信息的地层压力矩阵。

1.1 地层压力矩阵的概念

地层压力矩阵是指由一口井的目标层段埋藏深度数组H和相应的压力数组P构成的二维矩阵。如式(1)所示。根据地层压力类型，地层压力矩阵包括地层孔隙压力矩阵、地层坍塌压力矩阵和地层破裂压力矩阵。

地层压力矩阵HP由地层深度矩阵H和压力矩阵P构成，深度矩阵H为目标层段内相应地层埋深hi构成的矩阵，压力矩阵P为相应埋深hi处的地层压力 pi构成的矩阵，如图 1 所示。Hx(k－1)P、HxkP、Hx(k+1)P分别表示x井相邻的(k－1)、k、(k+1)地层单元的地层压力矩阵和表示k地层单元的顶、底界埋深。

由于地层压力具有一定的不确定性，相关研究［5-7］指出，用具有概率信息的区间代替单一数值的地层压力，可以考虑不确定性因素对地层压力预测精度的影响。因此，将压力矩阵P以考虑概率信息的离散化压力数值赋值，建立含不确定性信息的地层压力矩阵，

式中，pij为地层深度hi处将地层压力概率信息离散化后的压力数值。

由于含不确定性信息的地层压力矩阵能够较好地将实际地层压力控制在其区间范围内，因此它能够更加准确地描述地层压力在该地层层段内的分布情况。

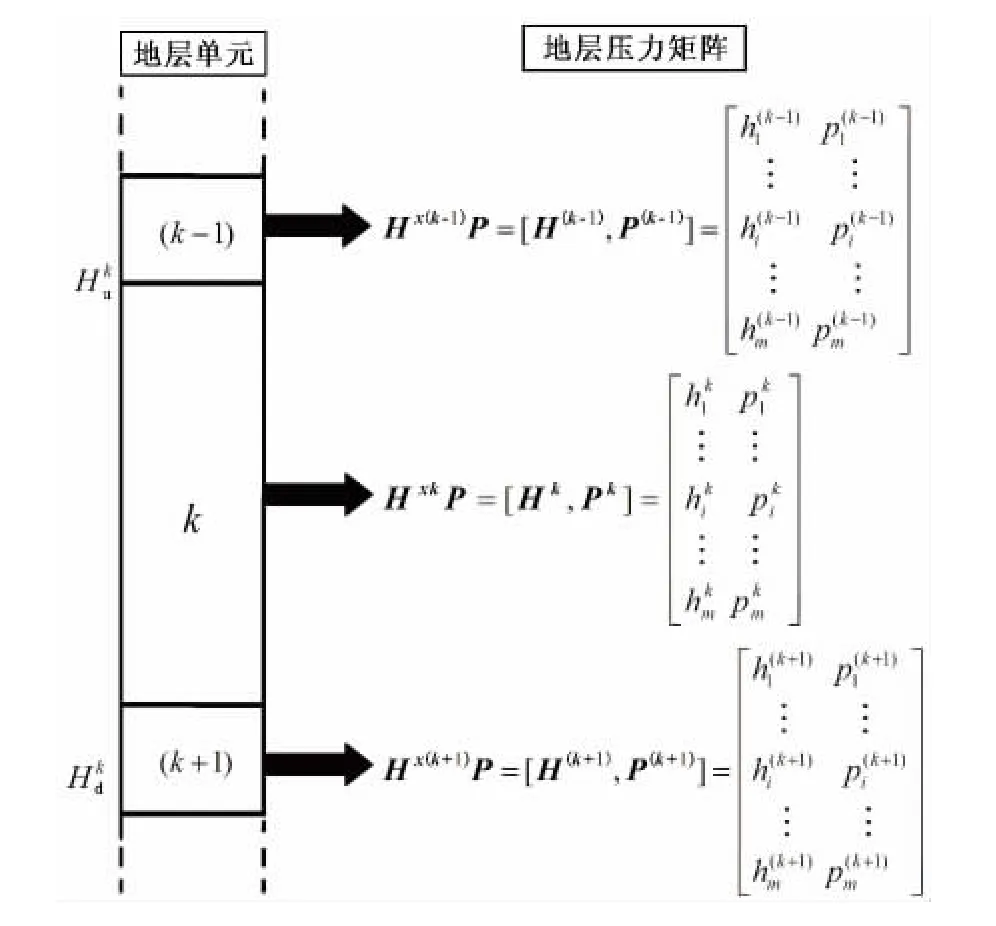
图1 地层压力矩阵与地层单元对应关系Fig.1 Corresponding relationship of formation pressure matrix and stratigraphic unit

1.2 地层压力矩阵的建立过程

地层压力矩阵包含两个信息，一是地层埋深信息，二是相应埋藏深度处的地层压力。因此，建立地层压力矩阵实质上是通过相关资料确定目标井的地质分层和地层压力，通过矩阵理论方法构建相应的矩阵。对于已钻井，地质分层信息可以通过井史资料获得，地层压力可以通过地震资料、测井资料或录井等资料计算得到。本文中以地层孔隙压力矩阵为例，描述利用测井资料建立压力矩阵的过程。

1.2.1 地层孔隙压力计算方法

利用声波测井资料监测地层孔隙压力是最常用的方法。大量试验研究表明，影响声波在岩石中传播速度的主要因素为岩性、孔隙度和垂直有效应力。若地层岩性均一，则声波速度主要是孔隙度和垂直有效应力的函数。对于仍处于原始加载应力状态下的正常压实和欠压实泥岩地层，其孔隙度又是垂直有效应力的函数。文献［8］中建立了声波速度与垂直有效应力的函数关系，表达式为

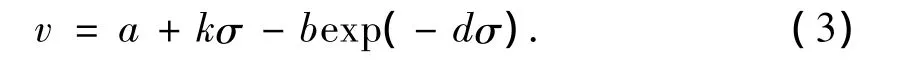
式中，v为声波速度，km/s;σ为垂直有效应力，MPa;a、k、b和 d 为模型系数。

计算出有效应力后，计算深度hi处的地层孔隙压力pi:

式中，Go为上覆岩层压力，MPa。

1.2.2 考虑不确定性的地层孔隙压力计算方法

由于地层压力具有一定不确定性，文献［9］中通过分析Eaton方法［10］中伊顿指数的不确定性，建立了含可信度的地层孔隙压力计算方法，表达式为

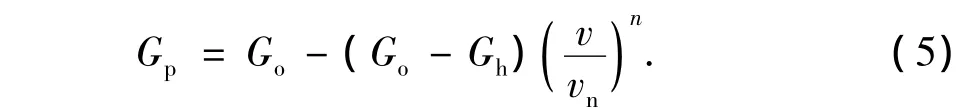
式中，Gh为静液柱压力，MPa;vn为正常压实条件下的声波速度，km/s。

在正常压实条件下，vn可以通过式(3)和式(4)联合计算:

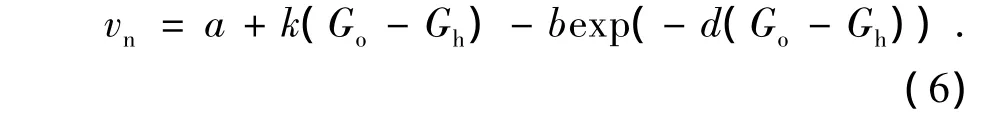
通过含可信度的地层孔隙压力分析可以获得赋存概率信息的离散化地层孔隙压力数值。Mote-Carlo方法［11］的基本理论是利用随机数模拟模型结果，非常适合赋存概率信息离散化地层孔隙压力的获取。步骤如下:

(1)分析伊顿指数的区域特性和概率分布特征，产生符合其自身概率分布的随机数，假设满足精度要求的模拟次数为N，则伊顿指数样本为X=［x1，x2，…，xN］;

(2)将伊顿指数样本代入伊顿公式进行计算，获得地层孔隙压力样本Y= ［y1，y2，…，yN］。对地层孔隙压力样本Y进行统计分析，剔除小概率样本值，可以得到深度hi处的地层孔隙压力pi。

1.2.3 地层孔隙压力矩阵的建立

对目标井井筒资料进行分析，获得地质分层信息，通过以上地层孔隙压力计算方法，可以利用目标地层的测井资料求取地层孔隙压力。将目标地层的深度矩阵H和孔隙压力矩阵P按照式(1)或式(2)的形式重构，建立地层孔隙压力矩阵HP。

2 待钻井地层压力矩阵的计算方法

以含不确定性信息的地层孔隙压力矩阵为例，假设某构造区域上有N口已钻邻井，通过地层孔隙压力矩阵构建方法，建立这N口井在目标地层的地层孔隙压力矩阵，利用以下理论方法和步骤建立待钻井在目标地层的地层孔隙压力矩阵。

2.1 待钻井地层剖面划分

地形生成技术［12］是GIS(geographic information system)的重要研究领域之一，它主要研究数字地形模型DTM(digital terrain model)的简化、生成和显示。利用地形生成技术的相关研究方法建立区域内岩层的空间分布，是区域地层压力描述的重要基础。

通过对已钻井的测井资料、岩性资料和地质信息的综合分析，获得已钻井井位部署、地质分层数据，然后利用地形生成技术建立区域的立体地层空间展布，根据待钻井的井位部署及其断层构造情况，分块分区域获得该构造区域内的邻井和待钻井位的地层划分情况。

第x口井的第k层顶界和底界埋深表示为Fxk=)(图2)，若整口井有M层分层，则该井地层剖面矩阵Fx和目标新井的地层剖面矩阵FT分别为

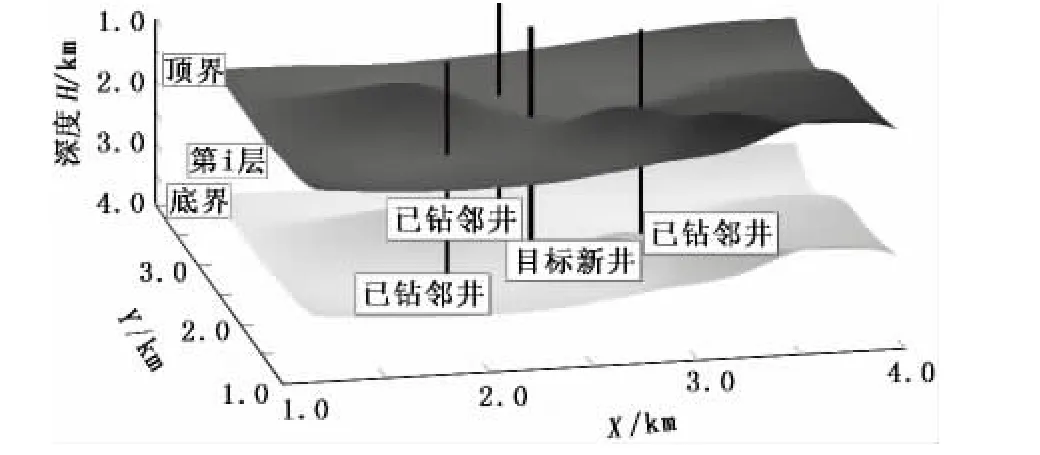
图2 区域地层空间分布示意图Fig.2 Sketch map of regional stratigraphic formation distribution

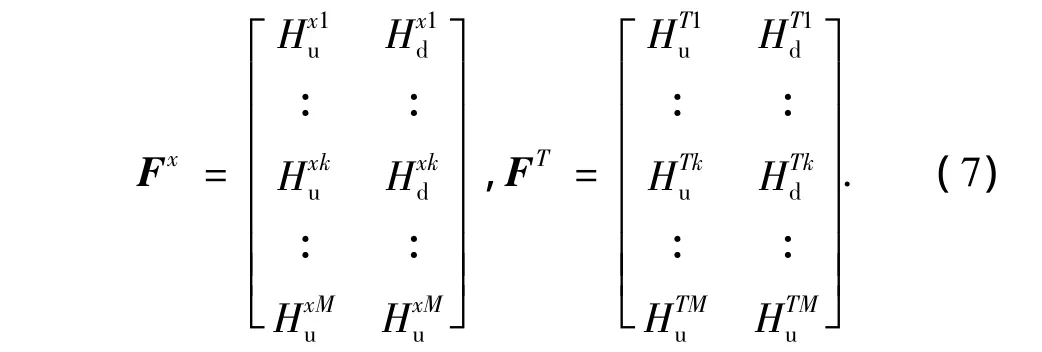
通过已钻井地质分层情况，在同一构造内，根据地层分布的连续性可以得到层位顶界和底界的等高线，因此可以得到待钻井的地质分层情况。

2.2 邻井地层压力矩阵深度平差处理

由于邻井和待钻井的第k层埋藏深度不一定相同，其厚度也不一定相等，因此需要对邻井在目标地层的地层压力矩阵进行处理，第x口井的经深度平差处理后的地层压力矩阵为

2.3 邻井地层压力矩阵空间插值处理

对于同一区块，假设岩层内部连续，同岩层为横向同性体。由于邻井与待钻井之间的距离不同，各井对于待钻井的地层压力影响不同，可以将距离作为加权因子。

假设有N口已钻邻井，并建立了各层段的地层压力矩阵，邻井井口平面坐标为(Xx，Yx)，x=1，2，…，N，待钻井的井口坐标为(XT，YT)，根据反距离加权插值(Shepard方法)［13］，第x口井在待钻井第k层的平均地层压力矩阵为

2.4 待钻井地层压力矩阵的建立

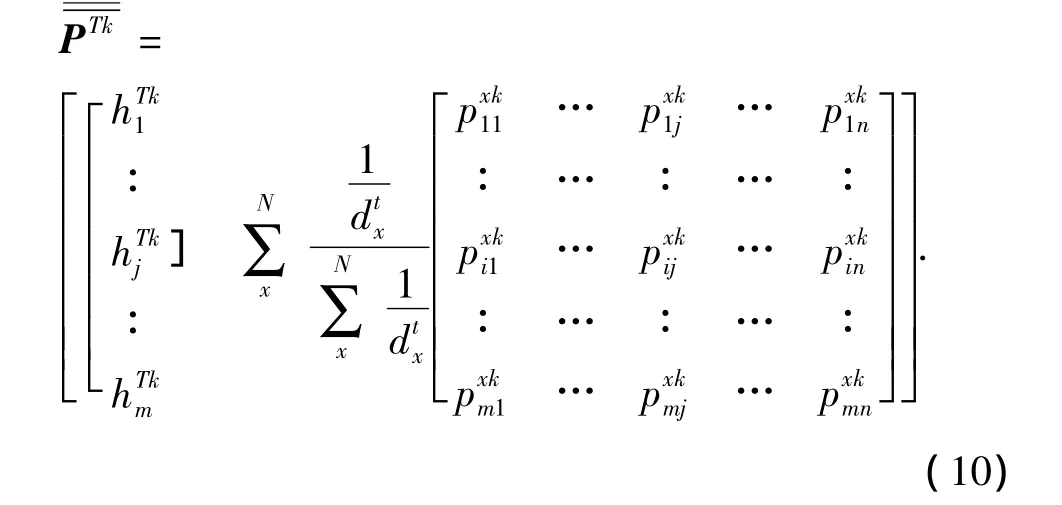
经过深度平差处理和距离加权修正后，由于深度和厚度的不同，各个已钻井地层压力矩阵中的地层深度矩阵经过深度变换后间距不相等，需要统一转换为待钻井地层深度矩阵，同时对压力矩阵的列向量进行插值处理。因此，经深度平差处理、加权修正和深度插值处理后，最后得到目标井第k层地层压力矩阵为

逐层求取地层压力矩阵后将各个矩阵按照地质分层顺序组装，得到待钻井全井段的地层压力矩阵。

由于地层压力矩阵包含丰富的压力信息，可以根据需要获得单值地层压力剖面或者不同可信度条件下的地层压力剖面。

3 算例分析

某构造区域有已钻直井5口，井位部署如图3所示，某地层顶、底界垂深见表1。选取T井为待钻井，A、B、C、D井为邻井。为验证本文建立的区域地层压力外延移植方法的可靠性，根据单值地层孔隙压力计算方法，利用测井资料求取了4口邻井在M地层的单值地层孔隙压力(图4(a))。

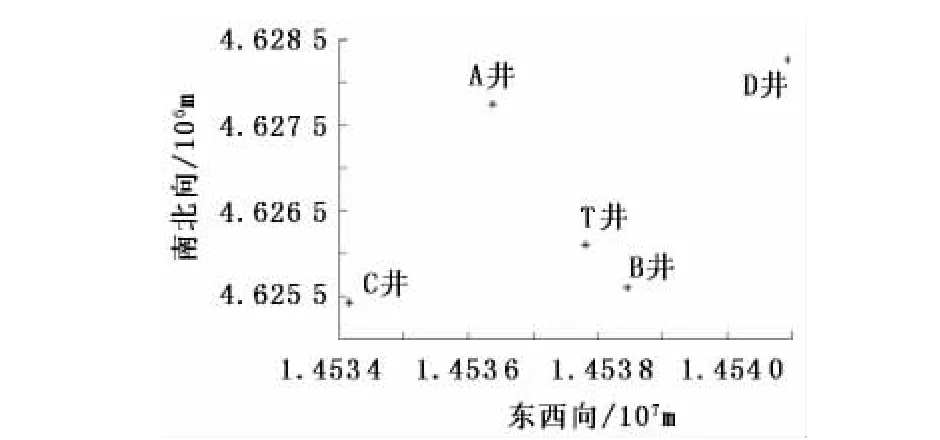
图3 井位部署Fig.3 Adjacent wells coordinate

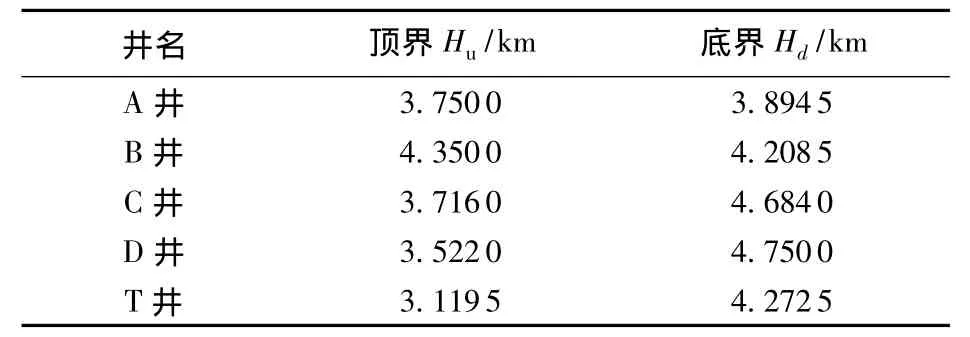
表1 地层顶、底界垂深Table 1 Vertical depth of a stratum bound

计算出各邻井的地层孔隙压力后，利用地层压力矩阵构建方法可以建立A、B、C、D井的地层孔隙压力矩阵。通过深度平差处理和空间插值处理，可得到4口邻井压力曲线分别移植到待钻井T井后在M地层的压力分布和考虑4口邻井的综合效果的T井压力移植曲线(图4(b))。利用邻井地层孔隙压力移植到待钻井的结果与该井完井后利用本井测井资料计算结果的对比如图5所示，对比结果表明最大相对误差为3.43%。

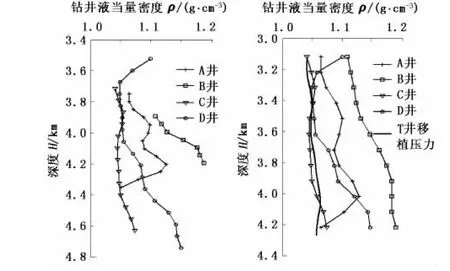
图4 邻井地层孔隙压力及其深度平差处理Fig.4 Formation pore pressure and its depth-adjustment results of adjacent wells

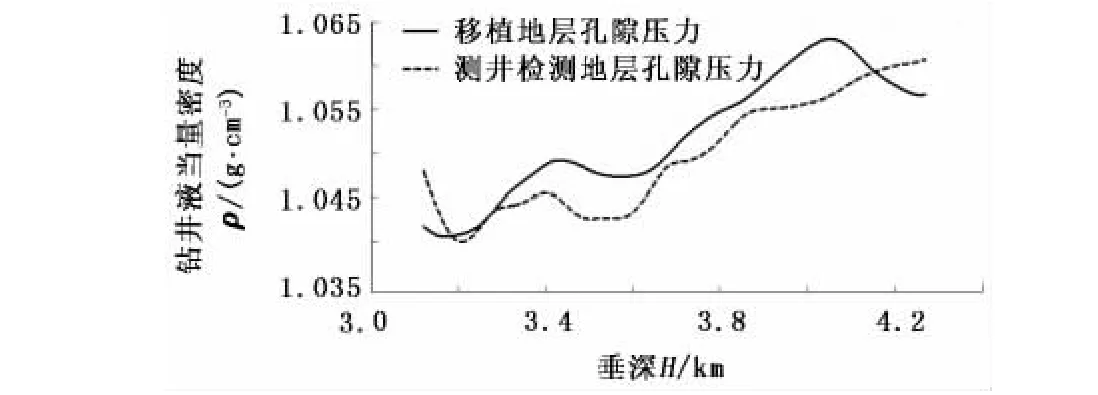
图5 邻井移植压力与测井检测压力对比Fig.5 Comparison of transplantation pressure and logging-detection pressure

4 结论

(1)通过引入地层压力矩阵，建立利用已钻井的井筒资料(测井、录井、钻井及地质等)构建待钻井的地层压力剖面的方法。由该方法得到的待钻井的地层孔隙压力值与该井完井后利用本井测井资料计算的压力值相比，最大相对误差为3.43%。

(2)邻井地层压力资料、邻井空间位置、目标区域空间连续性是影响地层压力外延移植方法计算精度的关键因素。对于存在断层或者地质构造比较复杂的地区，需要充分掌握地质构造特性，并借助地震资料分构造、分区块建立目标井的地层压力。

［1］ FERTL W H.Abnormal formation pressure，implication to exploration，drilling and production of oil and gas reservoirs［M］.Amsterdam:Elsevier，1976.

［2］ 钻井手册(甲方)编写组.钻井手册(甲方)上册［M］.北京:石油工业出版社，1990:43-86.

［3］ SAYERS C M，JOHNSON G M，DENYER G.Predrill pore pressure prediction using seismic data［R］.IADC/SPE 59122，2000.

［4］ 裴绪建，何启贤.利用邻井资料预测调整井地层压力［J］.断块油气田，1994(2):26-28.PEI Xu-jian，HE Qi-xian.Formation pressure prediction of adjustment wells using adjacent wells data［J］.Fault-Block Oil＆ Gas Field，1994(2):26-28.

［5］ NOBUO Morti A.Uncertainty analysis of borehole stability problems［R］.SPE 30502，1995.

［6］ da FONTOURA Sergio A B，HOLZBERGB Runo B，TEIXIRA Edson C，et al.Probabilistic analysis of wellbore stability during drilling［R］.SPE 78179，2002.

［7］ LIANG Q J.Application of quantitative risk analysis to pore pressure and fracture gradient prediction［R］.SPE 77354，2002.

［8］ 樊洪海.地层孔隙压力预测检测新方法与应用［D］.北京:石油大学石油工程学院，2001:92-99.FAN Hong-hai.New methods for prediction and evaluation of formation pore pressure［D］.College of Petroleum Engineering in University of Petroleum，China，2001:92-99.

［9］ 柯珂，管志川，周行.深水探井钻前含可信度的地层孔隙压力确立方法［J］.中国石油大学学报:自然科学版，2009，33(5):61-67.KE Ke，GUAN Zhi-chuan，ZHOU Hang.An approach to determining pre-drilling formation pore pressure with credibility for deep water exploration wells［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(5):61-67.

［10］ EATON Ben A.The equation for geopressure prediction from well logs［R］.SPE 5544，1975.

［11］ 卫军胡.蒙特卡洛方法在系统工程中的应用［M］.西安:西安交通大学出版社，2007.

［12］ 张继贤，柳健，李德仁.地形生成技术与方法的研究［J］.中国图像图形学报，1997(8/9):638-645.ZHANG Ji-xian，LIU Jian，LI De-ren.Technical approach to realistic terrain generation［J］.Jouranl of Image and Graphics，1997(8/9):638-645.

［13］ 张锦明，郭丽萍，张小丹.反距离加权插值算法中插值参数对DEM插值误差的影响［J］.测绘科学技术学报，2012(1):51-56.ZHANG Jin-ming，GUO Li-ping，ZHANG Xiao-dan.Effects of interpolation parameters in inverse distance weighted method on DEM accuracy［J］.Jouranl of Geomatics Science and Technology，2012(1):51-56.