分支井筒稳定的塑性力学模型及分析

张广清

(中国石油大学石油工程学院，北京 102249)

多分支井起源于20世纪30年代，1953年在苏联用涡轮钻具钻成第一口分支井，随后逐步推广到中东、南美、欧洲与亚洲［1］。国内外学者对分支井井壁稳定问题展开了广泛研究，Aadn∅y［2］和 Hoang［3］分别提出了分支井的二维与三维模型;Manriquez［4］、Fuentes［5］和 Manríquez［6］等运用有限元方法模拟了裸眼条件下分支井连接井段的稳定问题，Liu等［7］还考虑过地层流体作用。针对现有研究的不足，笔者考虑地层、水泥环和套管的弹塑性模型差异，建立弹塑性有限元模型，以中国东部油田的地应力特性为基础，分析不同分支井方位对井壁稳定性的影响。

1 分析模型

基本假设:① 岩层均质且各向同性;② 仅考虑应力场影响，不考虑温度场和渗流场影响;③ 不考虑材料的蠕变效应。

1.1 材料模型

介绍有关模型的基本控制方程方面的材料很多，Zienkiewicz等［8］结合有限元方法进行了全面讨论。本文中重点介绍使用的塑性模型，水泥环采用混凝土损伤塑性模型(CDP模型)，地层采用M-C塑性模型，套管采用Tresca弹塑性模型。水泥混凝土的塑性和脆性是材料两个方面的性质，采用的损伤塑性模型包含了低围压下的脆性和高围压下的延性特征。

(1)水泥环的混凝土损伤塑性模型(CDP模型)。CDP模型采用的是 Lubliner［9］提出的、由 Lee和Fenves［10］修正的屈服函数。用有效应力表示的屈服函数形式为

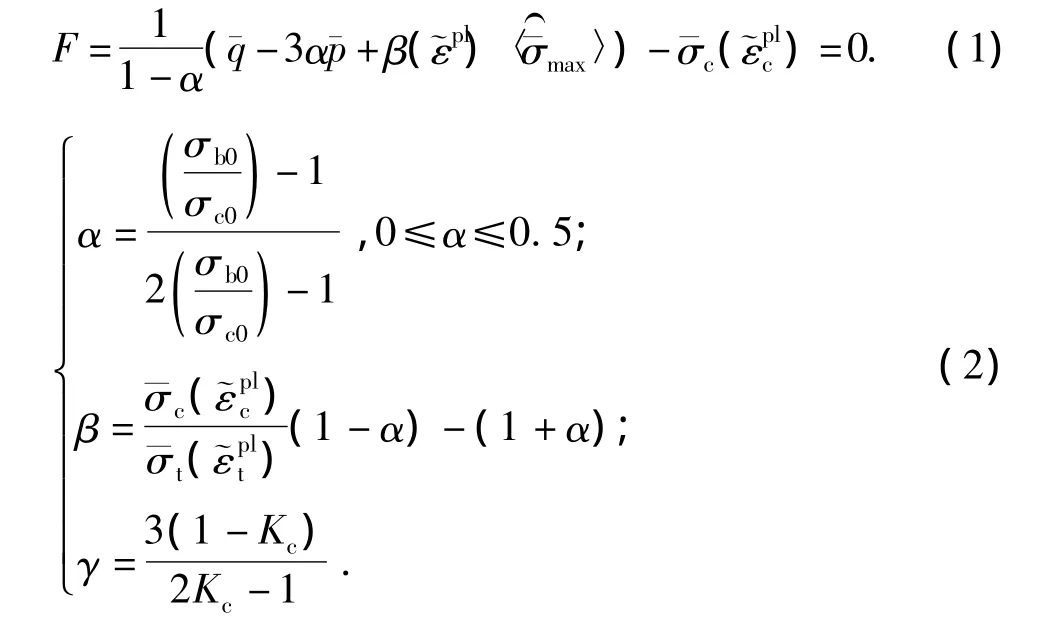
模型破坏包络线如图1所示。CDP模型采用各向同性损伤弹性和各向同性拉伸压缩塑性表示混凝土的非弹性行为［11］。两种破坏方式为拉伸破裂与压缩破坏，屈服面的变化规律主要由硬化参数和决定。

图1 混凝土破坏包络线Fig.1 Envelope of concrete failure

CDP模型可表示压缩和拉伸的塑性特征。图2为CDP模型的应力应变特征曲线。图2中OABI段为受拉屈服条件下的应力应变曲线，σto为无损伤条件下的抗拉屈服值，E0为无损伤条件下的弹性模量;左侧OK段虚线为无损伤前单轴受压条件下的应力应变曲线;BCEF段为受拉损伤后卸载并单轴加压条件下的应力应变曲线;FGH段为二次受压损伤后卸载并单轴受拉条件下的应力应变曲线。其中dt和dc分别为受拉损伤值与受压损伤值，它们是塑性应变、温度、与场变量的函数，当dt和dc的数值为0时，说明材料无损伤，当数值为1时，说明材料已经破坏;wt和wc分别为受拉和受压的刚度恢复值，它们是塑性应变、温度、与场变量的函数，当wt和wc的数值为0时，说明材料无任何刚度恢复，外载在拉压转换时弹性模量不会恢复到E0，当数值为1时，说明材料的弹性模量恢复到E0。

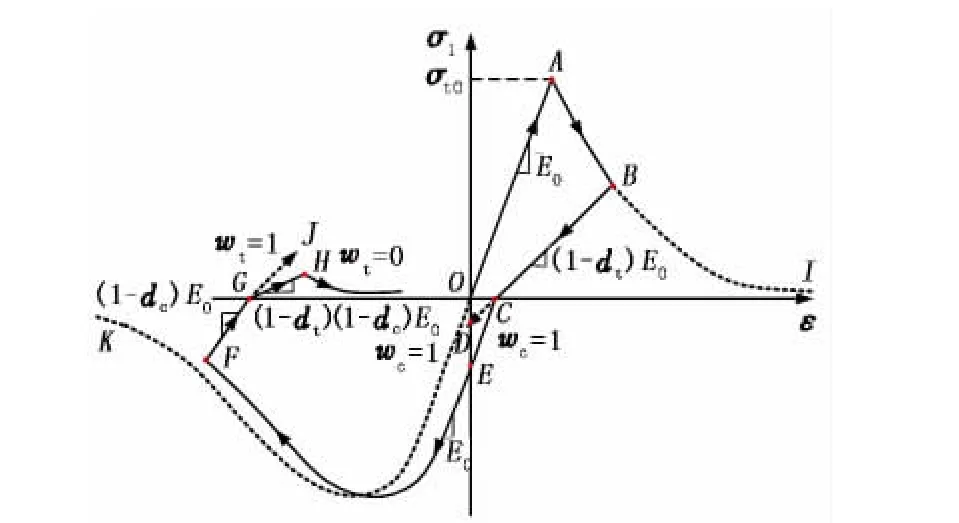
图2 CDP模型应力应变曲线Fig.2 Stress-strain curve of CDP model

(2)地层的MC塑性模型，

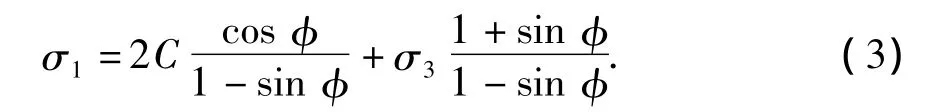
式中，σ1和σ3分别为最大和最小主应力，Pa;C为黏聚力，Pa;φ 为内摩擦角，(°)。(3)套管的理想弹塑性模型，

式中，σs为材料屈服应力，Pa。

通过API规范得到套管和水泥环的弹性参数，通过力学参数测试得到地层岩石参数和水泥环的压缩和拉伸塑性损伤参数。

J55套管弹性模量为210 GPa，泊松比为0.3，屈服应力为379 MPa;水泥环弹性模量为30 GPa，泊松比为 0.2，膨胀角 50°，Kc=1/3，fb0/fc0=1.15，其他材料参数见表1;地层弹性模量为11.1 GPa，泊松比为0.3，摩擦角为14.4°，黏聚力为34.8 MPa。

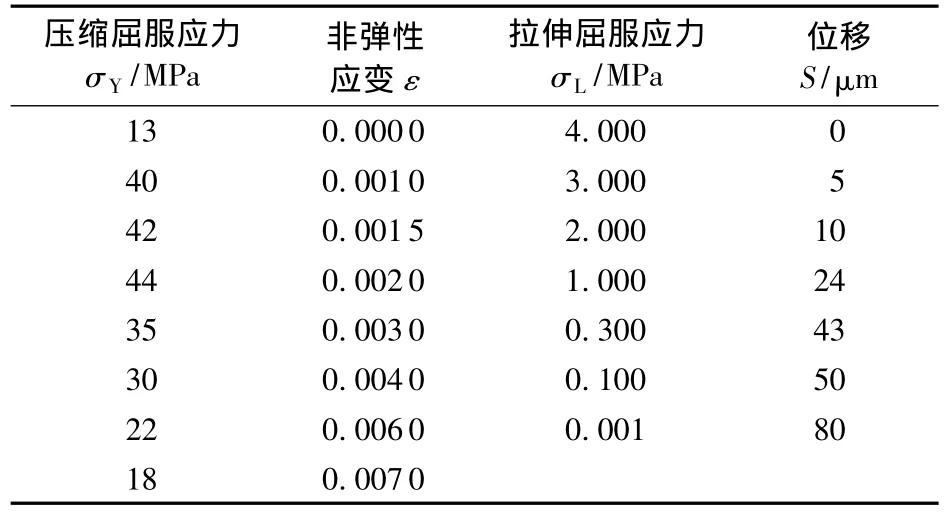
表1 CDP模型屈服参数Table 1 Yield parameters of CDP model

1.2 几何模型

由TAML分级体系［12］可知，从二级完井分支井开始，主井眼采用的都是固井完井，而国内外对二级以上分支井井身结构的认识不同，主要为两种结构形式［13］:①预留窗口式，分支井眼一般较小，多采用Φ 244.5 mm套管预留 Φ 114.3 mm窗口，钻 Φ 107.9 mm分支井眼;②套管侧钻式，主井眼Φ 339 mm，Φ 244.5 mm套管侧钻Φ 215.9 mm井眼，下Φ 139.7 mm套管。国内多采用后者，本文分析采用第二种井身结构设计。

进行非均匀地应力作用下的井壁稳定性分析时，由于同时考虑支井方位与应力夹角变化，因此一般采用长方体外部边界［5，14］，见图3。这样在三个相互垂直的矩形面上施加远场地应力，井壁上施加钻井液压力。支井方位变化后，几何模型变化，对应的网格也发生变化。这样每个支井方位的计算结果之间会存在模型网格差异造成的误差。一般将网格加密可减小网格引起的误差，但采用弹塑性计算模型会使计算时间大大增加。为此提出基于坐标变换的方法，采用圆柱状的几何外部边界，在外边界上施加变换后的应力分量。这样对不同的支井方位情况可以保持划分的网格不变，仅通过平面坐标变换获得新坐标系下应力分量值。只改变施加在柱状外表面的应力分量的大小和方向，消除不同支井方位情况下网格变化引起的误差，

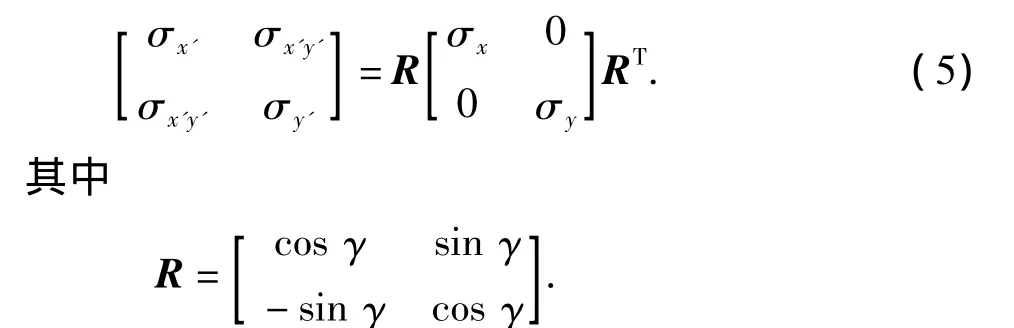
式中，γ为分支井方位角(分支井水平投影与水平最大主应力夹角)，(°);角标x、y表示转换前坐标系下参量;角标x'、y'表示转换后坐标系下参量。

考虑到边界效应的影响，模型整体高10 m，直径3 m，分支井的初始造斜角为3°，图4为建立的圆柱状几何模型。

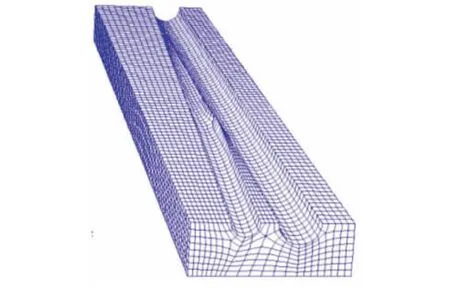
图3 分支井有限元几何模型的长方体外部边界Fig.3 Finite element geometry model of branch well with cuboid outer boundary

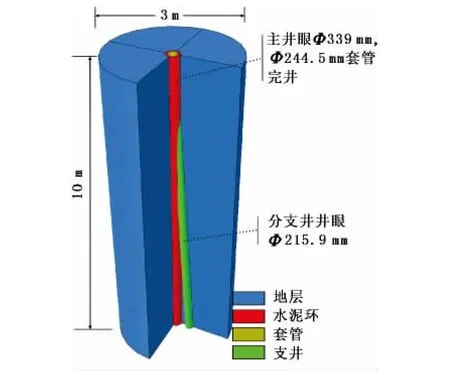
图4 分支井有限元几何模型的圆柱状外部边界Fig.4 Finite element geometry model of branch well with cylindrical outer boundary

1.3 地应力条件

地应力是油田开发和钻井方案设计的基础数据，也是影响井壁稳定的一个重要因素。葛洪魁等［15］根据渤海湾盆地油田水力压裂地应力测量资料，对地应力测量数据按深度进行线性回归，得到了中国东部油田的地应力分布规律，总体上三个主应力满足 σH＞σV＞ σh，σH、σh和 σV分别为最大、最小水平地应力和垂向地应力，MPa。通过式(2)可以获得分支段的初始地应力条件。

2 结果分析

根据材料弹塑性模型，输入对应的初始地应力条件、材料参数以及几何参数，通过数值软件Abaqus大量计算，可以获得模型的位移、应力和应变分布。通过分析当量应力和当量塑性应变，得到支井连接段各个位置的破坏情况，分析各因素对分支井井壁稳定性的影响。

主要分析分支井方位对分支井稳定性的影响。假定沿最大水平地应力方向支井方位角为0°。图5为支井方位角为45°情况下的整个模型、地层、套管、水泥环以及分支井井壁的位移、等效应力和塑性屈服区的分布。

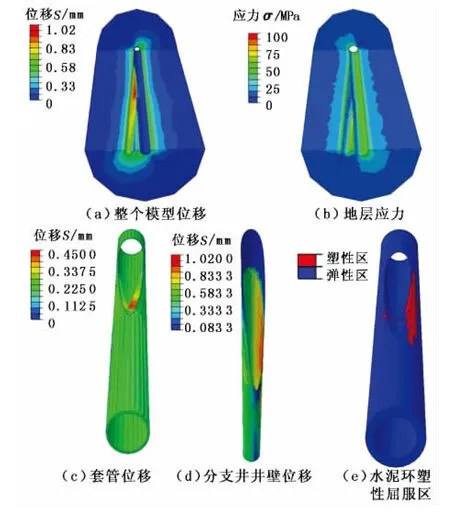
图5 支井方位角为45°时模型的部分计算结果Fig.5 Calculation results of numerical model of branch well azimuth angle 45°

从图5可以看出，支井的存在使模型的位移、应力应变分布非常复杂，但各个量的最大值均在支井连接部位或邻近部位。因此，采用水泥环-地层-套管作为整体研究对象分析支井井壁稳定性十分必要。

2.1 不同支井方位下的等效应力分布

等效应力即Mises应力，其最大值可以表示模型各位置处发生塑性变形或破坏的趋势和相对大小。假设其他参数保持不变，随着支井方位变化，水泥环-井壁-地层上的等效应力最大值的大小和位置也在不断变化，说明分支井失稳的规律受支井方位的影响。此处由于套管的强度远高于水泥环和地层，暂不讨论套管上的等效应力。

图6为不同支井方位下地层中等效应力分布。由图6看出，随着支井方位角增加(即由水平最大地应力方向逐渐变化到水平最小地应力方向)，等效应力的分布及最大值位置随之变化。支井方位角小于15°时最大等效应力在水平最小地应力方向上，即主井筒发生井壁失稳的趋势更大。当支井方位角达20°后，最大等效应力的位置由主井筒的水平最小地应力方向转移到分支井筒的连接部位下部，即支井筒发生井壁失稳的趋势更大。随着支井方位的增加，等效应力的最大值增大，表明随支井方位接近水平最小地应力方向，支井井壁失稳的趋势增加。图6表示的等效应力分布随支井方位的变化仅为变化趋势，无法表示具体数值的变化。图7为等效应力的最大值随支井方位的变化曲线。支井方位角的变化为5°，共有19种情况。将水泥环、地层和支井井壁上的等效应力最大值随支井方位的变化划分为5个阶段:

(1)当方位角小于15°时，水泥环、地层和支井井壁上的最大等效应力变化不大，且水泥环最大等效应力值大于地层和支井井壁的。从图6可知，此时地层的最大等效应力位置在主井筒的最小地应力方位上，因此支井井壁不会发生破坏。

(2)当方位角为15°～20°时，水泥环上的等效应力最大值减小，而地层和支井井壁上的等效应力最大值增大，且二者值逐渐接近。最大等效应力位置发生改变，转移到分支井连接处下部位置。

(3)当方位角为20°～35°时，分支井壁与岩层的最大等效应力变化趋势曲线基本重合，说明此时井壁上最大应力位于岩层上。

(4)当方位角为35°～40°时，水泥环上等效应力最大值增加速度加快，与支井井壁上的等效应力最大值重合，而地层中等效应力的最大值增加幅度减小，从与支井井壁的等效应力的最大值重合变为小于其数值。

(5)当方位角为40°～90°时，分支井壁与水泥环的最大等效应力变化趋势曲线完全重合，说明此时井壁上最大等效应力位于水泥环和支井井壁上。因此支井方位大于35°以后，最大等效应力位于分支井壁和水泥环，水泥环可以采用强度较高的材料，因而支井井壁发生破坏的趋势增加。

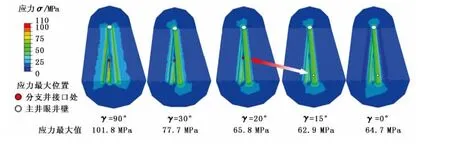
图6 地层最大等效应力分布Fig.6 Distribution of the maximum equivalent stress in rock

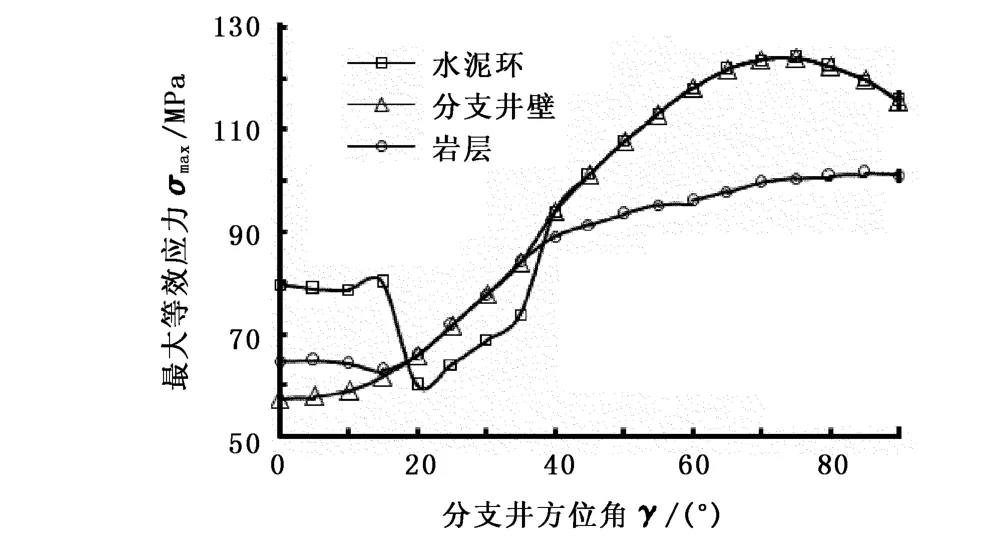
图7 最大等效应力随方位角的变化Fig.7 Variation of the maximum equivalent stress with azimuth angle

当方位角小于15°时，地层与水泥环最大等效应力位于主井筒上，这有利于分支井井眼稳定;随着方位角的增加，分支井井眼趋向于不稳定;当方位角为75°时，等效应力最大值位于分支井井壁上，不利于井壁稳定。

2.2 不同支井方位下的套管变形

由于套管的力学性能比地层和水泥环高出很多，分支井钻进过程中一般没有必要讨论套管的破坏问题。但套管对主井筒起到显著的支撑作用，使得支井钻进过程中地层和井筒的稳定性增强，尤其是对于分支井井壁稳定方面。

分支井钻井时在套管上形成不规则侧向开窗，该部位套管的应力集中增加，变形量也增加。套管开窗部分的变形量过大会造成钻进过程中套管局部破坏，影响正常钻进过程。

图8为不同支井方位下的套管开窗部位的变形。可以看出，套管变形量最大的位置在开窗部位的下端，该位置窗口的曲率半径小，应力集中程度大。当支井方位角为0°和90°时，变形关于开窗对称，随着支井方位变化，套管变形分布和最大值也发生变化。

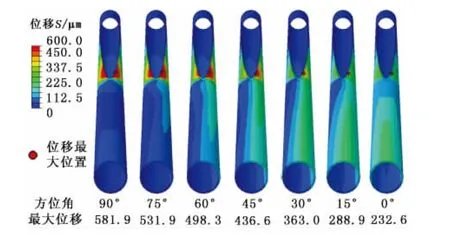
图8 套管的位移云图Fig.8 Displacement distribution of casing

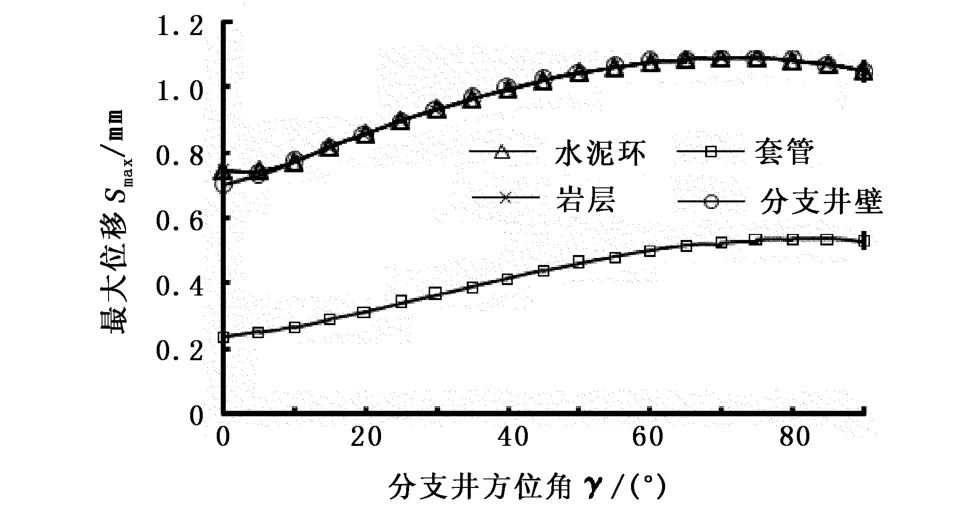
图9 最大位移随方位角的变化Fig.9 Variation of the maximum displacement with azimuth angle

图9为各部分变形量(位移)最大值随支井方位的变化。随方位角增大，各部分变形量最大值增大，70°时达到最大值，随后形变有所减小。在70°时套管最大变形量达到0.52 mm，由于窗口几何形状对称，则窗口变形量达到1.02 mm。这是假设开窗形状为理想光滑条件得出的，如果考虑开窗的实际形状，其窗口变形可达几个毫米，会造成钻进过程中套管局部破坏，影响正常钻进过程。因此，从套管侧窗变形的角度来看，分支井方位应该尽量靠近水平最大地应力方向。

2.3 不同支井方位下的水泥环塑性应变分布

地层、套管、水泥环和钻进中的支井形成了一个受力变形系统，其中一部分的破坏会导致其他部分的破坏。主井眼的水泥环在支井钻进过程中是否破坏对支井井壁的稳定也很重要。主井眼的水泥环破坏后，分支井连接部位及支井井壁更容易产生破坏。主井眼水泥环的受力和套管类似，但其力学参数和模型不同。

水泥环采用混凝土损伤塑性模型(CDP模型)，可以模拟产生的拉伸和压缩破坏，为了直观表示水泥环的破坏区分布，采用塑性应变表示其破坏。图10为不同支井方位对应的水泥环上的塑性应变分布，图中的红色表示发生塑性变形的部分。可以看出，水泥环上的塑性应变分布随支井方位变化。支井方位角为0°时，水泥环塑性区最小，分布在开窗下部的两侧，15°～60°时水泥环塑性区增加，塑性区主要分布在开窗右侧;75°～90°时水泥环塑性区出现在开窗两侧，且分布范围占据开窗部位的大部分。

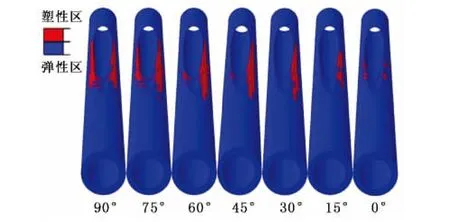
图10 水泥环塑性变形区Fig.10 Plastic deformation zone of cement

图11为水泥环中塑性应变最大值随支井方位的变化。可以看出，水泥环中塑性应变最大值随支井方位先增大后减小，在50°时对应最大值0.006。

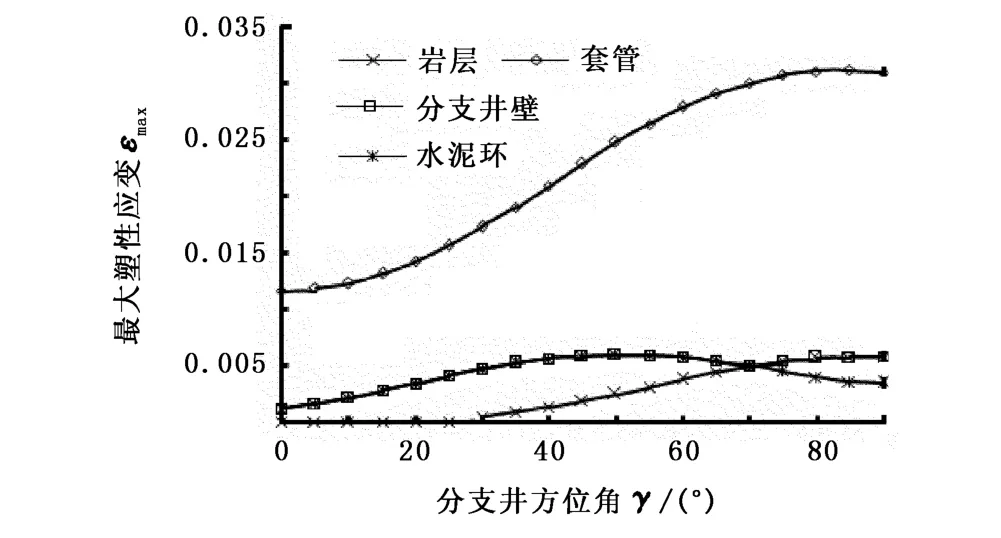
图11 最大塑性应变随方位角的变化Fig.11 Variation of the maximum plastic strain with azimuth angle

根据图10得到的水泥环塑性变形范围和图11得到的塑性变形的最大值，可以对水泥环破坏进行综合判断。当支井方位角大于30°时，主井眼水泥环出现的破坏可引起支井钻进问题，如支井或连接部位的坍塌。虽然支井方位角大于70°以后水泥环的塑性应变的最大值明显下降，但塑性应变的范围大大增加，同样会引起支井钻进问题。

当支井方位角小于25°时，地层和分支井壁的塑性应变不产生塑性变形，而后随着支井方位角的增大而增大。这也说明支井方位角小于30°可明显降低支井钻进过程中井壁失稳问题。

3 结论

(1)水泥环-地层-套管-井筒系统对分支井连接部位的稳定性影响显著，相比裸眼假设更接近钻井工程实际情况。

(2)建立的三维弹塑性有限元模型，将水泥环、地层和套管分别视为不同的塑性材料，同时建立了各向异性地层中应力分量转换方法，得到不随支井方位变化的有限元几何模型，消除了不同支井方位之间的模型误差。

(3)当支井方位角小于15°时，地层与水泥环最大等效应力位于主井筒上，有利于分支井井眼稳定;随着支井方位角的增加，分支井井眼趋向于不稳定;当方位角为75°时，等效应力最大值位于分支井井壁上，不利于井壁稳定。

(4)当支井方位角为70°时套管开窗部位的最大变形达到1.02 mm，从套管侧窗变形的角度来看，分支井方位应该尽量靠近水平最大地应力方向。

(5)当支井方位角大于30°时，主井眼水泥环出现的破坏可引起支井钻进问题，如支井或连接部位的坍塌。支井方位角大于70°以后水泥环的塑性应变的最大值明显下降，但塑性应变的范围大大增加，同样会引起支井钻进问题。

(6)综合当量应力、套管变形和水泥环塑性变形分布，认为在分支井井身结构设计中，为保证分支井井壁的稳定应采用较小方位角，同时避免采用50°～80°的分支井方位，以保证水泥环-地层-套管-井筒系统的稳定性和安全性。

［1］ 郑毅，黄伟和，鲜保安.国外分支井技术发展综述［J］. 石油钻探技术，1997，25(4):53-55.ZHENG Yi，HUANG Wei-he，XIAN Bao-an.Review the development of branch well technology overseas［J］.Journal of Petroleum Drilling Techniques，1997，25(4):53-55.

［2］ AADNΦ Y B S，EDLAND C.Borehole stability of multilateral junctions［R］.SPE 56757，1999.

［3］ HOANG S，ABOUSLEIMAN Y，AL-TAHINI A M.Multilaterals drilling and sustainable openhole production from theory to field-case studies［R］.SPE 116138-PA，2010.

［4］ MANRÍQUEZ A L，PODIO A L，SEPEHRNOORI K.Modeling of stability of junctions in multilateral wells using finite element:the 42nd US Rock Mechanics Symposium(USRMS)，San Francisco，CA，June 29-July 2，2008［R］.American Rock Mechanics Association，2008.

［5］ FUENTES J A，ECONOMIDES M J，CARBONELL R S.Stability of junctures for multilateral/multibranched wells［R］.SPE 57279，1999.

［6］ MANRIQUEZ A L，PODIO A，SEPEHRNOORI K.Modeling of the stability of multibranch horizontal open holes［R］.SPE 114117-MS，2008.

［7］ LIU J X，LIU J，ZHU W C，et al.Simulation of borehole failure with impact of mud permeation at multilateral junction［R］.SPE 88605，2004.

［8］ ZIENKIEWICZ O C，TAYLOR R L.The finite element method［J］.Butterworth-Heinemann，2000，4(23):71-73.

［9］ LUBLINER J，OLIVER J，OLLER S，et al.A plasticdamage model for concrete［J］.International Journal of Solids and Structures，1989，25(3):299-326.

［10］ LEE J，FENVES G L.Plastic-damage model for cyclic loading of concrete structures［J］.Journal of Engineering Mechanics，1998，124:892-900.

［11］ INC A.Abaqus analysis user1s manual［R］.Rising Sun Mills:SIMULIA，2010.

［12］ DIGGINS E.A proposed multi-lateral well classification matrix［J］.World Oil，1997，11(218):107.

［13］ 安克，王敏生.胜利油田分支井钻井技术现状及展望［J］.石油钻探技术，2003，31(6):7-9.AN Ke，WANG Min-sheng.Shengli Oilfield branch wells drilling technology present situation and prospects［J］.Journal of Petroleum Drilling Techniques，2003，31(6):7-9.

［14］ PAPANASTASIOU P，SIBAI M，HEILAND J，et al.Stability of a multilateral junction:experimental results and numerical modeling ［R］.SPE/ISRM 78212，2002.

［15］ 葛洪魁，林英松.油田地应力的分布规律［J］.断块油气田，1998，5(5):1-5.GE Hong-kui，LIN Ying-song.In-situ stress distribution law of oil field［J］.Journal of Fault-Block Oil＆ Gas Field，1998，5(5):1-5.