莱芜市人口的具有外生变量的时间序列预测模型
2013-10-22赵宪民
赵宪民
(莱芜职业技术学院机电工程系,山东 莱芜 271100)
0 前 言
时间序列是按照时间顺序取得的一系列观察值,时间序列数据的本质特征就是相邻观察值之间的依赖性。所以在对时间序列数据进行分析时,一般的回归模型难以体现变量自身前后及应变量与自变量过去的依赖关系。ARIMA模型是对变量自身前后依赖性进行分析的技术,它描述了变量自身当前与过去的统计依赖关系,在显示变量的动态系统(dynamical system)演变规律方面有着较为丰富的结构。但是由于ARIMA模型没有考虑其它变量对应变量的作用,所以也无法表达系统中变量间相互影响的关系。传递函数模型可在一定程度上弥补这两种模型的欠缺,并且模型构造灵活,可以用较少的参数建立阶数较高的模型。
国内外诸多学者对人口问题进行了广泛的研究,常见的有依据社会人口结构的Keyfitz矩阵方程模型、Lesilie矩阵方程模型、人口发展方程和指数方程模型及Logistic模型等[1-3]。对于时间序列模型,陈爱莲、安和平[4]、赵进文[5]、张慧芳[6]等用不同的方法对中国人口总量进行了探讨,都得到了较好的预测效果。
对于有关经济增长、经济发展与人口增长的关系问题,国内外学者进行了大量的实证研究,大都采用简单相关与回归分析方法来揭示其存在的关系。赵文进[5]、王谦[6]、郭震威[7]都指出虽然经济增长(GDP)与人口增长之间存在着很强的相关性,但并不是简单的线性关系,并不能采用简单的线性回归模型来揭示经济增长与人口之间的相互影响。并与众多文献一样,认为目前我们还很难计算经济增长与人口的数量关系。基于此,我们不妨考虑将经济增长量作为外生变量添加到人口时间序列模型中。本文就以莱芜市人口总量和GDP总量为例,建立含有外生变量的人口时间序列预测模型,并对模型的精确度进行检验,及对莱芜市未来几年人口进行预测。
1 ARIMA模型的介绍
1970年Box和Jenkins提出ARIMA (autoregressive integrated moving average)模型,也称为Box-Jenkins法[8]。该模型适用于非平稳时间序列,应用中需要通过若干次差分将非平稳时间序列转化为平稳时间序列,再对此平稳时间序列进行定阶和参数估计,得到(p,q)的值,然后就可以应用ARIMA(p,d,q)模型,其中p为模型的自回归项数,q为模型的滑动平均项数,d为时间序列成为平稳之前必须做差分的次数。本质上来说ARIMA模型是将时间序列平稳化后由ARMA模型来处理是一相同过程。
从定义上来说即是:一个非平稳时间序列Yi,通过 ▽Yt=Yt-Yt-1,▽2Yt= ▽(▽Yt)= ▽(Yt-Yt-1),……等依次差分成平稳时间序列Wt,使得Wt满足ARMA(p,q)模型:

且φ(B)=0与θ(B)=0所有根的模大于1;φ1,φ2,…,φp为自回归参数;θ1,θ2,…θq为滑动平均参数;随机项et为服从0均值、方差为σ2e且互相独立的白噪声序列;则称Wt为综合自回归移动平均序列,即ARIMA(p,d,q),所以ARIMA模型的一般形式为:
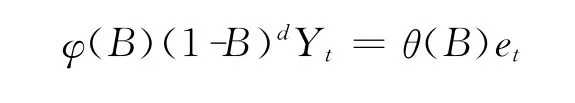
2 数据的处理
莱芜市1990年至2011年的人口总量和GDP总量数据来自于莱芜市统计年鉴[9]。记莱芜市人口总量序列为{Yt},GDP总量序列为{Xt},如图1和图2所示。从图1和图2中可以看出,两序列都具有明显的增长趋势,它是非平稳的,需要对其进行平稳化处理。
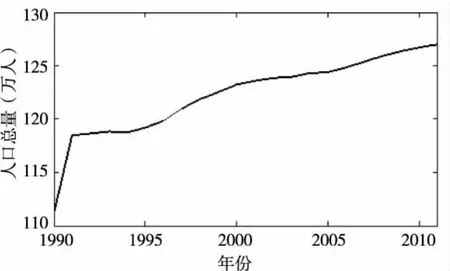
图1 1990—2011年莱芜市人口总量
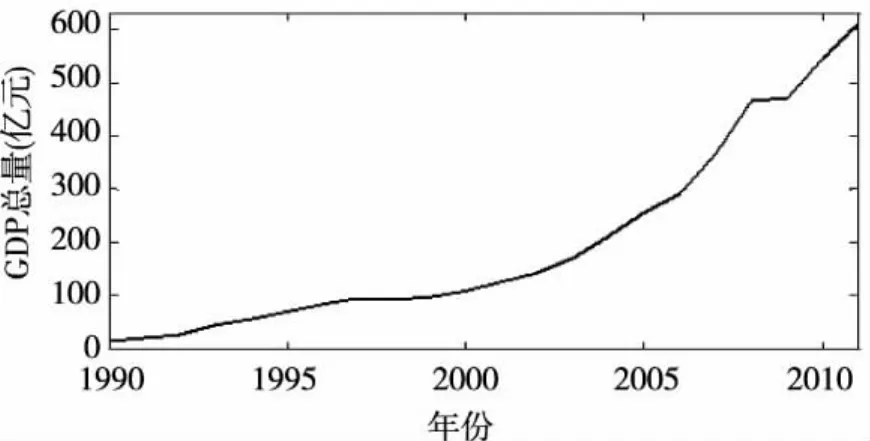
图2 1990—2011年莱芜市GDP总量
2.1 平稳化处理
根据1987—2009年数据自身特点及建模的需要,通过对莱芜市人口总量序列进行二次差分,对莱芜市GDP总量序列进行对数变换后二次差分得到平稳时间序列,即

其中▽是差分算子,Yt表示第t年莱芜市的人口总量;Xt表示第t年莱芜市的GDP总量。变换数据如图3和图4所示。

图3 莱芜市人口总量平稳化处理序列图
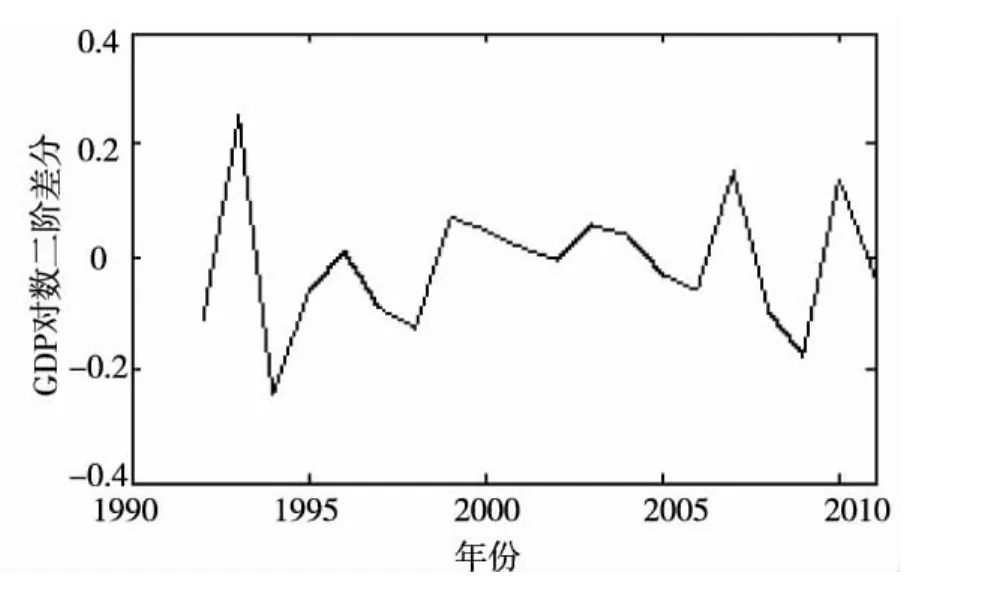
图4 莱芜市GDP总量平稳化处理序列图
传递函数模型为:

其中,ω(B)=α1B+α2B+…+αsB,δ(B)=β1B+β2B+…+βrB,Nt是噪声序列,可用ARMA模型描述为:Nt=φ(B)-1θ(B)et,式中,φ(B)、θ(B)是B的多项式,et是白噪声序列。
2.2 平稳序列的检验
如果数据序列是非平稳的,如存在一定的增长或下降趋势等,则需对数据进行差分或滑动平均法处理,使得数据平稳。一般采用ADF(augment Dickey-Fuller test)检验定量检验变换序列的平稳性,即先拟合序列的适应模型,然后求由该模型的参数组成的特征方程的特征根。

表1 莱芜市人口总量平稳化ADF检验结果
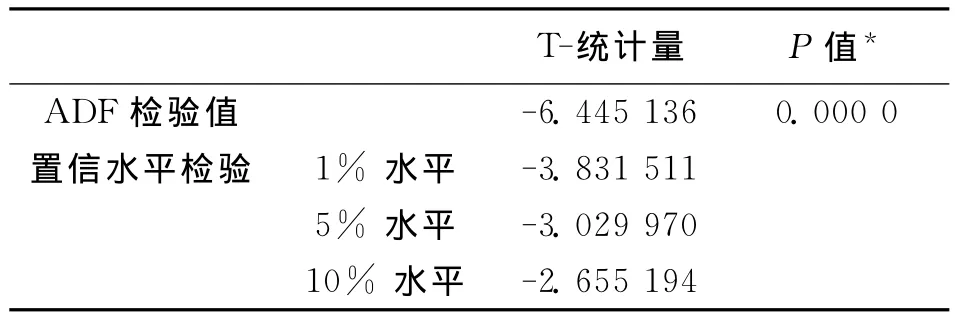
表2 莱芜市GDP总量平稳化ADF检验结果
由表1可知,对莱芜市人口总量平稳化后ADF检验统计量为-13.312 94,小于给出的1%~10%的临界值,所以拒绝原假设,说明序列不存在单位根,即该序列是平稳的。同理,莱芜市GDP总量平稳化后ADF检验统计量为-6.445 136,介于1%~5%水平之间,在给定的α=0.05显著性水平下,依然拒绝原假设,认为该序列是平稳的,可以建模使用。
3 模型阶数的确定与参数估计
对模型阶数的确定采用AIC和BIC准则进行定阶。AIC和BIC准则定义为
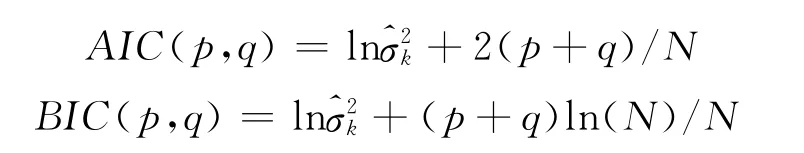
其中,是模型中噪声项方差的最小二乘估计,N为样本容量。若
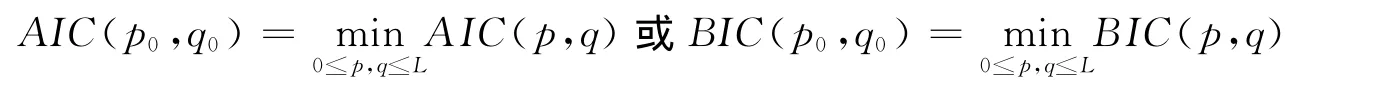
则确定 ARMA 模型阶数为 (p0,q0)[8]。
在AIC和BIC准则下,运用Eviews软件求得在所有p,q组合情况下对应的AIC和BIC值,通过比较得出,当莱芜市人口总量的滞后阶数p=2,q=1时,AICmin=0.4681,BICmin=0.6165。故初步判定莱芜市人口总量滞后阶数p=2,q=1。同理初步确定莱芜市GDP总量滞后阶数p=1。
由以上分析初步建立模型为:

将▽2Yt记为Wt,▽2lnXt记为Vt则上式可简写为

根据建立的模型,运用EViews软件对参数进行估计,具体结果见表3。
由表3最后一列中的p值可知,在显著性水平α=0.05下,各变量的系数均是显著的。因此建立的含外生变量时间序列模型为

4 模型的自适应检验

将式 (1)还原为实际人口总量数据和GDP总量数据模型为:

根据建立以上建立的含有外生变量的时间序列模型[11],对莱芜市2002-2011年总人口拟合,计算结果见表4。

表4 基于ARIMA (2,2,1)模型对莱芜市2002-2011年人口总量拟合
从表4中可以看出模型拟合的相对误差在0.7%以下,拟合效果较为理想。
5 模型的应用
由于GDP作为外生变量,若要对未来人口总量进行预测,需要知道未来几年的GDP总量。在此,根据已平稳化的GDP序列数据,采用时间序列模型对未来GDP总量进行预测。表5给出了利用所建立含外生变量的时间序列模型预测[12]莱芜市2010-2016年人口总量及其增长速度的计算结果。此外,算得莱芜市 “十二五”期间 (2011—2015年)人口总量的平均增长速度约为0.4万人。

表5 莱芜市2010-2016年人口总量及其增长速度
6 结 论
本文针对莱芜市地方人口总量的发展趋势,结合其与GDP总量的关系建立了含有外生变量的时间序列模型,拟合相对误差普遍在0.7%以下。表明人口总量与GDP总量之间有直接的依存关系,一定程度上揭示了人口增长与经济增长的关系。因此建立以GDP总量为外生变量的人口总量时间序列预测模型是合理的。
根据净增人口序列{Yt-Yt-1}可知,莱芜市总人口在1990-2001年平均每年增量在1.1万左右,2002年以后人口增量有所下降,平均在0.4万人左右。莱芜市 “十二五”期间人口总量年净增人口和环比增长速度分别稳定在0.4万人和0.3%左右,人口总规模将近130万。结果反映出党和国家的计划生育政策和促进中部崛起计划在莱芜市得到了贯彻落实。
[1]宋健,田雪原,于景元,等.人口预测和人口控制[M].北京:人民出版社,1982:30-50.
[2]李永胜.人口统计学[M].成都:西南财经大学出版社,2001:7-34.
[3]王彦,马伯强.20世纪80年代以来我国人口发展的数学模型与展望[J].北京大学学报:自然科学版(增刊),2003,39(12):28-33.
[4]陈爱莲,安和平.中国人口时间序列预测模型的探讨[J].人口与经济,2004,(06):65-69.
[5]赵进文.中国人口总量与GDP总量关系模型研究[J].中国人口科学,2003,(03):25-31.
[6]张慧芳,张德生,武新乾,等.我国人口总量的非参数预测模型[J].延边大学学报:自然科学版,2007,33(02):90-93.
[7]王谦,郭震威.人口增长对经济增长的影响分析——与胡鞍钢博士商榷[J].人口研究,2000,25(01):20-23.
[8]王振龙.时间序列分析[M].北京:中国统计出版社,2000:28-56.
[9]莱芜市统计局.莱芜市统计年鉴2009[M].北京:中国统计出版社,2009:1-27.
[10]易丹辉.数据分析与EVIEWS应用[M].北京:中国统计出版社,2002:17-63.
[11]陈泽中,李铎,杨启智,中国人均 GDP(1952-2002)时间序列分析[J].统计与决策,2005,(02):61-62.
[12]张晓峒.计量经济分析[M].上海:经济科学出版社,2000:20-80.
